Pentellated 6-Cubes

Orthogonal projections in B₆ Coxeter plane
6-cube	6-orthoplex	Pentellated 6-cube
Pentitruncated 6-cube	Penticantellated 6-cube	Penticantitruncated 6-cube
Pentiruncitruncated 6-cube	Pentiruncicantellated 6-cube	Pentiruncicantitruncated 6-cube
Pentisteritruncated 6-cube	Pentistericantitruncated 6-cube	Omnitruncated 6-cube

In six-dimensional geometry, a pentellated 6-cube is a convex uniform 6-polytope with 5th order truncations of the regular 6-cube.

There are unique 16 degrees of pentellations of the 6-cube with permutations of truncations, cantellations, runcinations, and sterications. The simple pentellated 6-cube is also called an expanded 6-cube, constructed by an expansion operation applied to the regular 6-cube. The highest form, the pentisteriruncicantitruncated 6-cube, is called an omnitruncated 6-cube with all of the nodes ringed. Six of them are better constructed from the 6-orthoplex given at pentellated 6-orthoplex.

Pentellated 6-cube

Pentellated 6-cube
Type	Uniform 6-polytope
Schläfli symbol	t_0,5{4,3,3,3,3}
Coxeter-Dynkin diagram
5-faces
4-faces
Cells
Faces
Edges	1920
Vertices	384
Vertex figure	5-cell antiprism
Coxeter group	B₆, [4,3,3,3,3]
Properties	convex

Alternate names

Pentellated 6-orthoplex
Expanded 6-cube, expanded 6-orthoplex
Small teri-hexeractihexacontitetrapeton (Acronym: stoxog) (Jonathan Bowers)^[1]

Images

Pentitruncated 6-cube

Pentitruncated 6-cube
Type	uniform 6-polytope
Schläfli symbol	t_0,1,5{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	8640
Vertices	1920
Vertex figure
Coxeter groups	B₆, [4,3,3,3,3]
Properties	convex

Alternate names

Teritruncated hexeract (Acronym: tacog) (Jonathan Bowers)^[2]

Images

orthographic projections
Coxeter plane	B₆	B₅	B₄
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B₃	B₂
Graph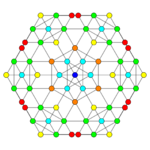
Dihedral symmetry	[6]	[4]
Coxeter plane	A₅	A₃
Graph
Dihedral symmetry	[6]	[4]

Penticantellated 6-cube

Penticantellated 6-cube
Type	uniform 6-polytope
Schläfli symbol	t_0,2,5{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	21120
Vertices	3840
Vertex figure
Coxeter groups	B₆, [4,3,3,3,3]
Properties	convex

Alternate names

Terirhombated hexeract (Acronym: topag) (Jonathan Bowers)^[3]

Images

orthographic projections
Coxeter plane	B₆	B₅	B₄
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B₃	B₂
Graph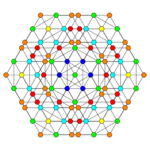
Dihedral symmetry	[6]	[4]
Coxeter plane	A₅	A₃
Graph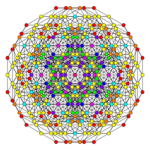
Dihedral symmetry	[6]	[4]

Penticantitruncated 6-cube

Penticantitruncated 6-cube
Type	uniform 6-polytope
Schläfli symbol	t_0,1,2,5{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	30720
Vertices	7680
Vertex figure
Coxeter groups	B₆, [4,3,3,3,3]
Properties	convex

Alternate names

Terigreatorhombated hexeract (Acronym: togrix) (Jonathan Bowers)^[4]

Images

orthographic projections
Coxeter plane	B₆	B₅	B₄
Graph
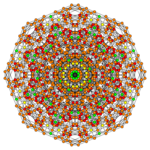
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B₃	B₂
Graph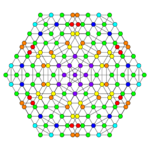
Dihedral symmetry	[6]	[4]
Coxeter plane	A₅	A₃
Graph
Dihedral symmetry	[6]	[4]

Pentiruncitruncated 6-cube

Pentiruncitruncated 6-cube
Type	uniform 6-polytope
Schläfli symbol	t_0,1,3,5{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	151840
Vertices	11520
Vertex figure
Coxeter groups	B₆, [4,3,3,3,3]
Properties	convex

Alternate names

Tericellirhombated hexacontitetrapeton (Acronym: tocrag) (Jonathan Bowers)^[5]

Images

orthographic projections
Coxeter plane	B₆	B₅	B₄
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B₃	B₂
Graph
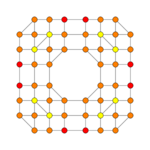
Dihedral symmetry	[6]	[4]
Coxeter plane	A₅	A₃
Graph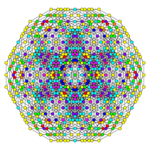
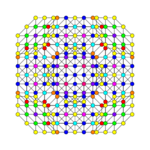
Dihedral symmetry	[6]	[4]

Pentiruncicantellated 6-cube

Pentiruncicantellated 6-cube
Type	uniform 6-polytope
Schläfli symbol	t_0,2,3,5{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	46080
Vertices	11520
Vertex figure
Coxeter groups	B₆, [4,3,3,3,3]
Properties	convex

Alternate names

Teriprismatorhombi-hexeractihexacontitetrapeton (Acronym: tiprixog) (Jonathan Bowers)^[6]

Images

Pentiruncicantitruncated 6-cube

Pentiruncicantitruncated 6-cube
Type	uniform 6-polytope
Schläfli symbol	t_0,1,2,3,5{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	80640
Vertices	23040
Vertex figure
Coxeter groups	B₆, [4,3,3,3,3]
Properties	convex

Alternate names

Terigreatoprismated hexeract (Acronym: tagpox) (Jonathan Bowers)^[7]

Images

orthographic projections
Coxeter plane	B₆	B₅	B₄
Graph
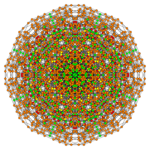
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B₃	B₂
Graph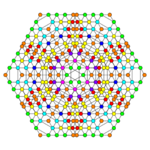
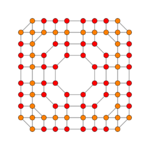
Dihedral symmetry	[6]	[4]
Coxeter plane	A₅	A₃
Graph
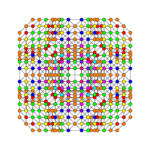
Dihedral symmetry	[6]	[4]

Pentisteritruncated 6-cube

Pentisteritruncated 6-cube
Type	uniform 6-polytope
Schläfli symbol	t_0,1,4,5{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	30720
Vertices	7680
Vertex figure
Coxeter groups	B₆, [4,3,3,3,3]
Properties	convex

Alternate names

Tericellitrunki-hexeractihexacontitetrapeton (Acronym: tactaxog) (Jonathan Bowers)^[8]

Images

Pentistericantitruncated 6-cube

Pentistericantitruncated 6-cube
Type	uniform 6-polytope
Schläfli symbol	t_0,1,2,4,5{4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	80640
Vertices	23040
Vertex figure
Coxeter groups	B₆, [4,3,3,3,3]
Properties	convex

Alternate names

Tericelligreatorhombated hexeract (Acronym: tocagrax) (Jonathan Bowers)^[9]

Images

orthographic projections
Coxeter plane	B₆	B₅	B₄
Graph
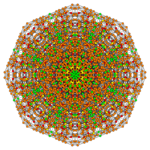
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B₃	B₂
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A₅	A₃
Graph
Dihedral symmetry	[6]	[4]

Omnitruncated 6-cube

Omnitruncated 6-cube
Type	Uniform 6-polytope
Schläfli symbol	t_0,1,2,3,4,5{3⁵}
Coxeter-Dynkin diagrams
5-faces	728: 12 t_0,1,2,3,4{3,3,3,4} 60 {}×t_0,1,2,3{3,3,4} 40px×40px 160 {6}×t_0,1,2{3,4} 40px×40px 240 {8}×t_0,1,2{3,3} 40px×40px 192 {}×t_0,1,2,3{3³} 40px×40px 64 t_0,1,2,3,4{3⁴}
4-faces	14168
Cells	72960
Faces	151680
Edges	138240
Vertices	46080
Vertex figure	irregular 5-simplex
Coxeter group	B₆, [4,3,3,3,3]
Properties	convex, isogonal

The omnitruncated 6-cube has 5040 vertices, 15120 edges, 16800 faces (4200 hexagons and 1260 squares), 8400 cells, 1806 4-faces, and 126 5-faces. With 5040 vertices, it is the largest of 35 uniform 6-polytopes generated from the regular 6-cube.

Alternate names

Pentisteriruncicantituncated 6-cube or 6-orthoplex (omnitruncation for 6-polytopes)
Omnitruncated hexeract
Great teri-hexeractihexacontitetrapeton (Acronym: gotaxog) (Jonathan Bowers)^[10]

Images

Full snub 6-cube

The full snub 6-cube or omnisnub 6-cube, defined as an alternation of the omnitruncated 6-cube is not uniform, but it can be given Coxeter diagram and symmetry [4,3,3,3,3]⁺, and constructed from 12 snub 5-cubes, 64 snub 5-simplexes, 60 snub tesseract antiprisms, 192 snub 5-cell antiprisms, 160 3-sr{4,3} duoantiprisms, 240 4-s{3,4} duoantiprisms, and 23040 irregular 5-simplexes filling the gaps at the deleted vertices.

Related polytopes

These polytopes are from a set of 63 uniform 6-polytopes generated from the B₆ Coxeter plane, including the regular 6-cube or 6-orthoplex.

Notes

↑ Klitzing, (x4o3o3o3o3x - stoxog)
↑ Klitzing, (x4x3o3o3o3x - tacog)
↑ Klitzing, (x4o3x3o3o3x - topag)
↑ Klitzing, (x4x3x3o3o3x - togrix)
↑ Klitzing, (x4x3o3x3o3x - tocrag)
↑ Klitzing, (x4o3x3x3o3x - tiprixog)
↑ Klitzing, (x4x3x3o3x3x - tagpox)
↑ Klitzing, (x4x3o3o3x3x - tactaxog)
↑ Klitzing, (x4x3x3o3x3x - tocagrax)
↑ Klitzing, (x4x3x3x3x3x - gotaxog)

References

H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN:978-0-471-01003-6 [1]
  - (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  - (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
Klitzing, Richard. "6D uniform polytopes (polypeta)". https://bendwavy.org/klitzing/dimensions/polypeta.htm. x4o3o3o3o3x - stoxog, x4x3o3o3o3x - tacog, x4o3x3o3o3x - topag, x4x3x3o3o3x - togrix, x4x3o3x3o3x - tocrag, x4o3x3x3o3x - tiprixog, x4x3x3o3x3x - tagpox, x4x3o3o3x3x - tactaxog, x4x3x3o3x3x - tocagrax, x4x3x3x3x3x - gotaxog

External links

Glossary for hyperspace, George Olshevsky.
Polytopes of Various Dimensions
Multi-dimensional Glossary

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform 4-polytope	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

0.00

(0 votes)

Original source: https://en.wikipedia.org/wiki/Pentellated 6-cubes. Read more

[1] Klitzing, (x4o3o3o3o3x - stoxog)

[2] Klitzing, (x4x3o3o3o3x - tacog)

[3] Klitzing, (x4o3x3o3o3x - topag)

[4] Klitzing, (x4x3x3o3o3x - togrix)

[5] Klitzing, (x4x3o3x3o3x - tocrag)

[6] Klitzing, (x4o3x3x3o3x - tiprixog)

[7] Klitzing, (x4x3x3o3x3x - tagpox)

[8] Klitzing, (x4x3o3o3x3x - tactaxog)

[9] Klitzing, (x4x3x3o3x3x - tocagrax)

[10] Klitzing, (x4x3x3x3x3x - gotaxog)