Cantellated 7-Cubes
 From Handwiki
From Handwiki 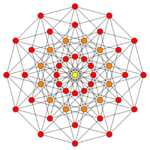 7-cube |
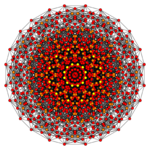 Cantellated 7-cube |
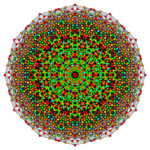 Bicantellated 7-cube |
 Tricantellated 7-cube |
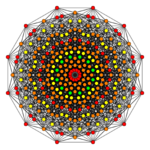 Birectified 7-cube |
 Cantitruncated 7-cube |
 Bicantitruncated 7-cube |
 Tricantitruncated 7-cube |
 Cantellated 7-orthoplex |
 Bicantellated 7-orthoplex |
 Cantitruncated 7-orthoplex |
 Bicantitruncated 7-orthoplex |
| Orthogonal projections in B6 Coxeter plane | |||
|---|---|---|---|
In seven-dimensional geometry, a cantellated 7-cube is a convex uniform 7-polytope, being a cantellation of the regular 7-cube.
There are 10 degrees of cantellation for the 7-cube, including truncations. 4 are most simply constructible from the dual 7-orthoplex.
Cantellated 7-cube
| Cantellated 7-cube | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | rr{4,3,3,3,3,3} |
| Coxeter diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 16128 |
| Vertices | 2688 |
| Vertex figure | |
| Coxeter groups | B7, [4,3,3,3,3,3] |
| Properties | convex |
Alternate names
- Small rhombated hepteract (acronym: sersa) (Jonathan Bowers)[1]
Images
Bicantellated 7-cube
| Bicantellated 7-cube | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | r2r{4,3,3,3,3,3} |
| Coxeter diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 40320 |
| Vertices | 6720 |
| Vertex figure | |
| Coxeter groups | B7, [4,3,3,3,3,3] |
| Properties | convex |
Alternate names
- Small birhombated hepteract (acronym: sibrosa) (Jonathan Bowers)[2]
Images
Tricantellated 7-cube
| Tricantellated 7-cube | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | r3r{4,3,3,3,3,3} |
| Coxeter diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 47040 |
| Vertices | 6720 |
| Vertex figure | |
| Coxeter groups | B7, [4,3,3,3,3,3] |
| Properties | convex |
Alternate names
- Small trirhombihepteractihecatonicosoctaexon (acronym: strasaz) (Jonathan Bowers)[3]
Images
Cantitruncated 7-cube
| Cantitruncated 7-cube | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | tr{4,3,3,3,3,3} |
| Coxeter diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 18816 |
| Vertices | 5376 |
| Vertex figure | |
| Coxeter groups | B7, [4,3,3,3,3,3] |
| Properties | convex |
Alternate names
- Great rhombated hepteract (acronym: gersa) (Jonathan Bowers)[4]
Images
It is fifth in a series of cantitruncated hypercubes:
Bicantitruncated 7-cube
| Bicantitruncated 7-cube | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | r2r{4,3,3,3,3,3} |
| Coxeter diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 47040 |
| Vertices | 13440 |
| Vertex figure | |
| Coxeter groups | B7, [4,3,3,3,3,3] |
| Properties | convex |
Alternate names
- Great birhombated hepteract (acronym: gibrosa) (Jonathan Bowers)[5]
Images
Tricantitruncated 7-cube
| Tricantitruncated 7-cube | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t3r{4,3,3,3,3,3} |
| Coxeter diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 53760 |
| Vertices | 13440 |
| Vertex figure | |
| Coxeter groups | B7, [4,3,3,3,3,3] |
| Properties | convex |
Alternate names
- Great trirhombihepteractihecatonicosoctaexon (acronym: gotrasaz) (Jonathan Bowers)[6]
Images
Related polytopes
These polytopes are from a family of 127 uniform 7-polytopes with B7 symmetry.
See also
- List of B7 polytopes
Notes
- ↑ Klitizing, (x3o3x3o3o3o4o - sersa)
- ↑ Klitizing, (o3x3o3x3o3o4o - sibrosa)
- ↑ Klitizing, (o3o3x3o3x3o4o - strasaz)
- ↑ Klitizing, (x3x3x3o3o3o4o - gersa)
- ↑ Klitizing, (o3x3x3x3o3o4o - gibrosa)
- ↑ Klitizing, (o3o3x3x3x3o4o - gotrasaz)
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN:978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "7D uniform polytopes (polyexa)". https://bendwavy.org/klitzing/dimensions/polyexa.htm. x3o3x3o3o3o4o- sersa, o3x3o3x3o3o4o - sibrosa, o3o3x3o3x3o4o - strasaz, x3x3x3o3o3o4o - gersa, o3x3x3x3o3o4o - gibrosa, o3o3x3x3x3o4o - gotrasaz
External links
- Polytopes of Various Dimensions
- Multi-dimensional Glossary
Fundamental convex regular and uniform polytopes in dimensions 2–10
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 |
Categories: [7-polytopes]
↧ Download as ZWI file | Last modified: 03/28/2025 04:15:52 | 5 views
☰ Source: https://handwiki.org/wiki/Cantellated_7-cubes | License: CC BY-SA 3.0
✘
ZWI is not signed. [what is this?]

 KSF
KSF