Steric 5-Cubes
 From Handwiki
From Handwiki
|
|
|
|
|
|
| Orthogonal projections in B5 Coxeter plane | ||
|---|---|---|
In five-dimensional geometry, a steric 5-cube or (steric 5-demicube or sterihalf 5-cube) is a convex uniform 5-polytope. There are unique 4 steric forms of the 5-cube. Steric 5-cubes have half the vertices of stericated 5-cubes.
Steric 5-cube
| Steric 5-cube | |
|---|---|
| Type | uniform polyteron |
| Schläfli symbol |
|
| Coxeter-Dynkin diagram | |
| 4-faces | 82 |
| Cells | 480 |
| Faces | 720 |
| Edges | 400 |
| Vertices | 80 |
| Vertex figure | {3,3}-t1{3,3} antiprism |
| Coxeter groups | D5, [32,1,1] |
| Properties | convex |
Alternate names
- Steric penteract, runcinated demipenteract
- Small prismated hemipenteract (siphin) (Jonathan Bowers)[1]:(x3o3o *b3o3x - siphin)
Cartesian coordinates
The Cartesian coordinates for the 80 vertices of a steric 5-cube centered at the origin are the permutations of
- (±1,±1,±1,±1,±3)
with an odd number of plus signs.
Images
| Coxeter plane | B5 | |
|---|---|---|
| Graph | 
| |
| Dihedral symmetry | [10/2] | |
| Coxeter plane | D5 | D4 |
| Graph | 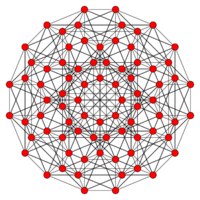
|
|
| Dihedral symmetry | [8] | [6] |
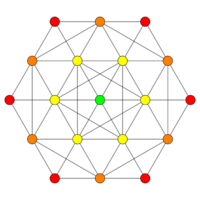
| Coxeter plane | D3 | A3 |
| Graph | 
|
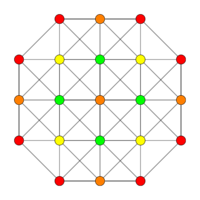
|
| Dihedral symmetry | [4] | [4] |
Related polytopes
Stericantic 5-cube
| Stericantic 5-cube | |
|---|---|
| Type | uniform polyteron |
| Schläfli symbol |
|
| Coxeter-Dynkin diagram | |
| 4-faces | 82 |
| Cells | 720 |
| Faces | 1840 |
| Edges | 1680 |
| Vertices | 480 |
| Vertex figure | |
| Coxeter groups | D5, [32,1,1] |
| Properties | convex |
Alternate names
- Prismatotruncated hemipenteract (pithin) (Jonathan Bowers)[1]:(x3x3o *b3o3x - pithin)
Cartesian coordinates
The Cartesian coordinates for the 480 vertices of a stericantic 5-cube centered at the origin are coordinate permutations:
- (±1,±1,±3,±3,±5)
with an odd number of plus signs.
Images
| Coxeter plane | B5 | |
|---|---|---|
| Graph | 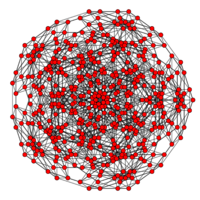
| |
| Dihedral symmetry | [10/2] | |
| Coxeter plane | D5 | D4 |
| Graph | 
|
|
| Dihedral symmetry | [8] | [6] |
| Coxeter plane | D3 | A3 |
| Graph | 
|

|
| Dihedral symmetry | [4] | [4] |
Steriruncic 5-cube
| Steriruncic 5-cube | |
|---|---|
| Type | uniform polyteron |
| Schläfli symbol |
|
| Coxeter-Dynkin diagram | |
| 4-faces | 82 |
| Cells | 560 |
| Faces | 1280 |
| Edges | 1120 |
| Vertices | 320 |
| Vertex figure | |
| Coxeter groups | D5, [32,1,1] |
| Properties | convex |
Alternate names
- Prismatorhombated hemipenteract (pirhin) (Jonathan Bowers)[1]:(x3o3o *b3x3x - pirhin)
Cartesian coordinates
The Cartesian coordinates for the 320 vertices of a steriruncic 5-cube centered at the origin are coordinate permutations:
- (±1,±1,±1,±3,±5)
with an odd number of plus signs.
Images
| Coxeter plane | B5 | |
|---|---|---|
| Graph | 
| |
| Dihedral symmetry | [10/2] | |
| Coxeter plane | D5 | D4 |
| Graph | 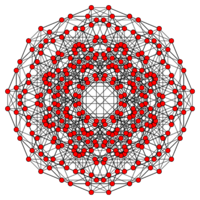
|
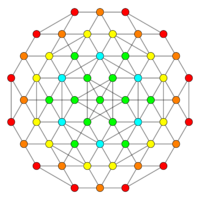
|
| Dihedral symmetry | [8] | [6] |
| Coxeter plane | D3 | A3 |
| Graph | 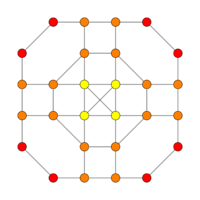
|
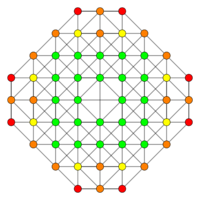
|
| Dihedral symmetry | [4] | [4] |
Steriruncicantic 5-cube
| Steriruncicantic 5-cube | |
|---|---|
| Type | uniform polyteron |
| Schläfli symbol |
|
| Coxeter-Dynkin diagram | |
| 4-faces | 82 |
| Cells | 720 |
| Faces | 2080 |
| Edges | 2400 |
| Vertices | 960 |
| Vertex figure | |
| Coxeter groups | D5, [32,1,1] |
| Properties | convex |
Alternate names
- Great prismated hemipenteract (giphin) (Jonathan Bowers)[1]:(x3x3o *b3x3x - giphin)
Cartesian coordinates
The Cartesian coordinates for the 960 vertices of a steriruncicantic 5-cube centered at the origin are coordinate permutations:
- (±1,±1,±3,±5,±7)
with an odd number of plus signs.
Images
| Coxeter plane | B5 | |
|---|---|---|
| Graph | 
| |
| Dihedral symmetry | [10/2] | |
| Coxeter plane | D5 | D4 |
| Graph | 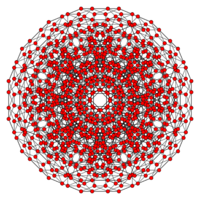
|
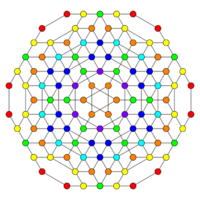
|
| Dihedral symmetry | [8] | [6] |
| Coxeter plane | D3 | A3 |
| Graph | 
|
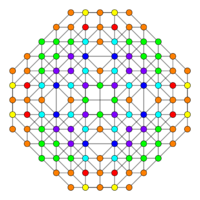
|
| Dihedral symmetry | [4] | [4] |
Related polytopes
This polytope is based on the 5-demicube, a part of a dimensional family of uniform polytopes called demihypercubes for being alternation of the hypercube family.
There are 23 uniform polytera (uniform 5-polytope) that can be constructed from the D5 symmetry of the 5-demicube, of which are unique to this family, and 15 are shared within the 5-cube family.
References
- ↑ 1.0 1.1 1.2 1.3 Klitzing, Richard. "5D uniform polytopes (polytera)". https://bendwavy.org/klitzing/dimensions/polytera.htm.
Further reading
- Coxeter, H. S. M. (1973). Regular Polytopes (3rd ed.). New York City: Dover. https://books.google.com/books?id=iWvXsVInpgMC. Retrieved 2022-05-19.
- Coxeter, H. S. M. (1995-05-17) (in en-CA). Kaleidoscopes: Selected Writings of H.S.M. Coxeter. Canadian Mathematical Society Series of Monographs and Advanced Texts. John Wiley & Sons. ISBN 978-0-471-01003-6. OCLC 632987525. http://www.wiley.com/WileyCDA/WileyTitle/productCd-0471010030.html. Retrieved 2022-05-19.
- Coxeter, H. S. M. (1940-12-01). "Regular and Semi Regular Polytopes I" (in en-CA). Mathematische Zeitschrift (Springer Nature) 46: 380–407. doi:10.1007/BF01181449. ISSN 1432-1823. https://link.springer.com/article/10.1007/BF01181449. Retrieved 2022-05-19.
- Coxeter, H. S. M. (1985-12-01). "Regular and Semi-Regular Polytopes II" (in en-CA). Mathematische Zeitschrift (Springer Nature) 188 (4): 559–591. doi:10.1007/BF01161657. ISSN 1432-1823. https://link.springer.com/article/10.1007/BF01161657. Retrieved 2022-05-19.
- Coxeter, H. S. M. (1988-03-01). "Regular and Semi-Regular Polytopes III" (in en-CA). Mathematische Zeitschrift (Springer Nature) 200 (1): 3–45. doi:10.1007/BF01161745. ISSN 1432-1823. https://link.springer.com/article/10.1007/BF01161745. Retrieved 2022-05-19.
- Johnson, Norman W. (1991). Uniform Polytopes (Unfinished manuscript thesis). Cite has empty unknown parameter:
|1=(help) - Johnson, Norman W. (1966). The Theory of Uniform Polytopes and Honeycombs (PhD thesis). University of Toronto. Retrieved 2022-05-19.
External links
- Weisstein, Eric W.. "Hypercube". http://mathworld.wolfram.com/Hypercube.html.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary
Fundamental convex regular and uniform polytopes in dimensions 2–10
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 |
Categories: [5-polytopes]
↧ Download as ZWI file | Last modified: 05/16/2025 10:26:24 | 6 views
☰ Source: https://handwiki.org/wiki/Steric_5-cubes | License: CC BY-SA 3.0
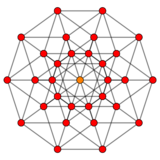



 KSF
KSF