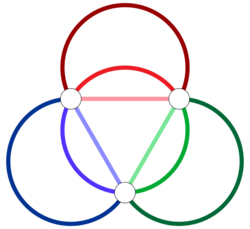
Shannon multigraph

In the mathematical discipline of graph theory, Shannon multigraphs, named after Claude Shannon by (Vizing 1965), are a special type of triangle graphs, which are used in the field of edge coloring in particular.

A Shannon multigraph is multigraph with 3 vertices for which either of the following conditions holds:

• a) all 3 vertices are connected by the same number of edges.
• b) as in a) and one additional edge is added.

More precisely one speaks of Shannon multigraph Sh(n), if the three vertices are connected by [math]\displaystyle{ \left\lfloor \frac{n}{2} \right\rfloor }[/math], [math]\displaystyle{ \left\lfloor \frac{n}{2} \right\rfloor }[/math] and [math]\displaystyle{ \left\lfloor \frac{n+1}{2} \right\rfloor }[/math] edges respectively. This multigraph has maximum degree n. Its multiplicity (the maximum number of edges in a set of edges that all have the same endpoints) is [math]\displaystyle{ \left\lfloor \frac{n+1}{2} \right\rfloor }[/math].

Examples

• Shannon multigraphs
• 

  Sh(2)

• 

  Sh(3)

• 

  Sh(4)

• 

  Sh(5)

• 

  Sh(6)

• 

  Sh(7)

Edge coloring

This nine-edge Shannon multigraph requires nine colors in any edge coloring; its vertex degree is six and its multiplicity is three.

According to a theorem of (Shannon 1949), every multigraph with maximum degree [math]\displaystyle{ \Delta }[/math] has an edge coloring that uses at most [math]\displaystyle{ \frac32\Delta }[/math] colors. When [math]\displaystyle{ \Delta }[/math] is even, the example of the Shannon multigraph with multiplicity [math]\displaystyle{ \Delta/2 }[/math] shows that this bound is tight: the vertex degree is exactly [math]\displaystyle{ \Delta }[/math], but each of the [math]\displaystyle{ \frac32\Delta }[/math] edges is adjacent to every other edge, so it requires [math]\displaystyle{ \frac32\Delta }[/math] colors in any proper edge coloring.

A version of Vizing's theorem (Vizing 1964) states that every multigraph with maximum degree [math]\displaystyle{ \Delta }[/math] and multiplicity [math]\displaystyle{ \mu }[/math] may be colored using at most [math]\displaystyle{ \Delta+\mu }[/math] colors. Again, this bound is tight for the Shannon multigraphs.

References

• Fiorini, S.; Wilson, Robin James (1977), Edge-colourings of graphs, Research Notes in Mathematics, 16, London: Pitman, p. 34, ISBN 0-273-01129-4 
• "A theorem on coloring the lines of a network", J. Math. Physics 28: 148–151, 1949, doi:10.1002/sapm1949281148 .
• Volkmann, Lutz (1996) (in German), Fundamente der Graphentheorie, Wien: Springer, p. 289, ISBN 3-211-82774-9 .
• "On an estimate of the chromatic class of a p-graph", Diskret. Analiz. 3: 25–30 .
• Vizing, V. G. (1965), "The chromatic class of a multigraph", Kibernetika 1965 (3): 29–39 .

External links

• Lutz Volkmann: Graphen an allen Ecken und Kanten. Lecture notes 2006, p. 242 (German)

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Shannon multigraph. Read more