Analytic Hierarchy Process
 From Citizendium - Reading time: 32 min
From Citizendium - Reading time: 32 min
The Analytic Hierarchy Process (AHP) is a structured technique for helping people deal with complex decisions. Rather than prescribing a "correct" decision, the AHP helps people to determine one that suits their needs and wants. Based on mathematics and psychology, it was developed by Thomas L. Saaty in the 1970s and has been extensively studied and refined since then. The AHP provides a comprehensive and rational framework for structuring a problem, for representing and quantifying its elements, for relating those elements to overall goals, and for evaluating alternative solutions. It is used throughout the world in a wide variety of decision situations, in fields such as government, business, industry, healthcare, and education.
Several firms supply computer software to assist in applying the process.
Users of the AHP first decompose their decision problem into a hierarchy of more easily comprehended sub-problems, each of which can be analyzed independently. The elements of the hierarchy can relate to any aspect of the decision problem—tangible or intangible, carefully measured or roughly estimated, well- or poorly-understood—anything at all that applies to the decision at hand.
Once the hierarchy is built, the decision makers systematically evaluate its various elements, comparing them to one another in pairs. In making the comparisons, the decision makers can use concrete data about the elements, or they can use their judgments about the elements' relative meaning and importance. It is the essence of the AHP that human judgments, and not just the underlying information, can be used in performing the evaluations.[1]
The AHP converts these evaluations to numerical values that can be processed and compared over the entire range of the problem. A numerical weight or priority is derived for each element of the hierarchy, allowing diverse and often incommensurable elements to be compared to one another in a rational and consistent way. This capability distinguishes the AHP from other decision-making techniques.
In the final step of the process, numerical priorities are derived for each of the decision alternatives. Since these numbers represent the alternatives' relative ability to achieve the decision goal, they allow a straightforward consideration of the various courses of action.
Uses and applications[edit]
While it can be used by individuals working on straightforward decisions, Analytic Hierarchy Process (AHP) is most useful where teams of people are working on complex problems, especially those with high stakes, involving human perceptions and judgments, whose resolutions have long-term repercussions.[2] It has unique advantages where important elements of the decision are difficult to quantify or compare, or where communication among team members is impeded by their different specializations, terminologies, or perspectives.
Decision situations to which the AHP can be applied include:
- Choice - The selection of one alternative from a given set of alternatives, usually where there are multiple decision criteria involved.
- Ranking - Putting a set of alternatives in order from most to least desirable
- Prioritization - Determining the relative merit of a set of alternatives, as opposed to selecting a single one or merely ranking them
- Resource allocation - Apportioning resources among a set of alternatives
- Benchmarking - Comparing the processes in one's own organization with those of other best-of-breed organizations
- Quality management - Dealing with the multidimensional aspects of quality and quality improvement
The applications of AHP to complex decision situations have numbered in the thousands,[3] and have produced extensive results in problems involving planning, resource allocation, priority setting, and selection among alternatives.[2] Other areas have included forecasting, total quality management, business process re-engineering, quality function deployment, and the Balanced Scorecard. Many AHP applications are never reported to the world at large, because they take place at high levels of large organizations where security and privacy considerations prohibit their disclosure. But some uses of AHP are discussed in the literature. Recently these have included:
- Deciding how best to reduce the impact of global climate change (Fondazione Eni Enrico Mattei)[4]
- Quantifying the overall quality of software systems (Microsoft Corporation)[5]
- Selecting university faculty (Bloomsburg University of Pennsylvania)[6]
- Deciding where to locate offshore manufacturing plants (University of Cambridge)[7]
- Assessing risk in operating cross-country petroleum pipelines (American Society of Civil Engineers)[8]
- Deciding how best to manage U.S. watersheds (U.S. Department of Agriculture)[3]
AHP is sometimes used in designing highly specific procedures for particular situations, such as the rating of buildings by historic significance.[9] It was recently applied to a project that uses video footage to assess the condition of highways in Virginia. Highway engineers first used it to determine the optimum scope of the project, then to justify its budget to lawmakers.[10]
AHP is widely used in countries around the world. At a recent international conference on AHP, over 90 papers were presented from 19 countries, including the U.S., Germany, Japan, Chile, Malaysia, and Nepal. Topics covered ranged from Establishing Payment Standards for Surgical Specialists, to Strategic Technology Roadmapping, to Infrastructure Reconstruction in Devastated Countries.[11] AHP was introduced in China in 1982, and its use in that country has expanded greatly since then—its methods are highly compatible with the traditional Chinese decision making framework, and it has been used for many decisions in the fields of economics, energy, management, environment, traffic, agriculture, industry, and the military.[12]
Though using AHP requires no specialized academic training, the subject is widely taught at the university level—one AHP software provider lists over a hundred colleges and universities among its clients.[13] AHP is considered an important subject in many institutions of higher learning, including schools of engineering[14] and graduate schools of business.[15] AHP is also an important subject in the quality field, and is taught in many specialized courses including Six Sigma, Lean Six Sigma, and QFD.[16][17][18]
In China, nearly a hundred schools offer courses in AHP, and many doctoral students choose AHP as the subject of their research and dissertations. Over 900 papers have been published on the subject in that country, and there is at least one Chinese scholarly journal devoted exclusively to AHP.[12]
Implementation[edit]

A typical device for entering judgments in a group decision making session
As will be shown in the examples that follow, using the AHP involves the mathematical synthesis of numerous judgments about the decision problem at hand. It is not uncommon for these judgments to number in the dozens or even the hundreds. While the math can be done by hand or with a calculator, it is far more common to use one of several computerized methods for entering and synthesizing the judgments. The simplest of these involve standard spreadsheet software, while the most complex use custom software, often augmented by special devices for acquiring the judgments of decision makers gathered in a meeting room.[19][20]
Steps in using the process[edit]
Model the problem as a hierarchy[edit]
The first step in the Analytic Hierarchy Process is to model the problem as a hierarchy. In doing this, participants explore the aspects of the problem at levels from general to detailed, then express it in the multileveled way that the AHP requires. As they work to build the hierarchy, they increase their understanding of the problem, of its context, and of each other's thoughts and feelings about both.[21]
Hierarchies defined
A hierarchy is a system of ranking and organizing people, things, ideas, etc., where each element of the system, except for the top one, is subordinate to one or more other elements. Diagrams of hierarchies are often shaped roughly like pyramids, but other than having a single element at the top, there is nothing necessarily pyramid-shaped about a hierarchy.
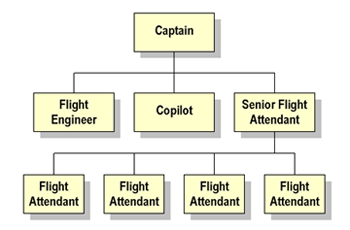
Human organizations are often structured as hierarchies. In the airliner example shown to the right, the hierarchical system is used for assigning responsibilities, exercising leadership, and facilitating communication.
Familiar hierarchies of "things" include a desktop computer's tower unit at the "top," with its subordinate monitor, keyboard, and mouse. Inside the tower is another hierarchy, with the top level motherboard and its subordinate hard drive(s), CD-ROM drive, and sometimes a floppy drive or DVD writer.
In the world of ideas, we use hierarchies to help us acquire detailed knowledge of complex reality: we structure the reality into its constituent parts, and these in turn into their own constituent parts, proceeding down the hierarchy as many levels as we care to. At each step, we focus on understanding a single component of the whole, temporarily disregarding the other components at this and all other levels. As we go through this process, we increase our understanding of whatever reality we are studying.
Think of the hierarchy that medical students use while learning anatomy—they separately consider the musculoskeletal system (including parts and subparts like the hand and its constituent muscles and bones), the circulatory system (and its many levels and branches), the nervous system (and its numerous components and subsystems), etc., until they've covered all the systems and the important subdivisions of each. Advanced students continue the subdivision all the way to the level of the cell or molecule. In the end, the students understand the "big picture" and a considerable number of its details. Not only that, but they understand the relation of the individual parts to the whole. By working hierarchically, they've gained a comprehensive understanding of anatomy.
Similarly, when we approach a complex decision problem, we can use a hierarchy to integrate large amounts of information into our understanding of the situation. As we build this information structure, we form a better and better picture of the problem as a whole.[21]
AHP hierarchies explained
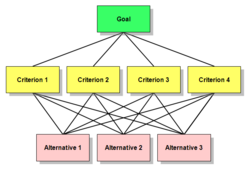
An AHP hierarchy is a structured means of modeling the problem at hand. It consists of an overall goal, a group of options or alternatives for reaching the goal, and a group of factors or criteria that relate the alternatives to the goal. The criteria can be further broken down into subcriteria, sub-subcriteria, and so on, in as many levels as the problem requires.
The hierarchy can be visualized as a diagram like the one below, with the goal at the top, the alternatives at the bottom, and the criteria in the middle. There are useful terms for describing the parts of such diagrams: Each box is called a node. The boxes descending from any node are called its children. The node from which a child node descends is called its parent. Groups of related children are called comparison groups. The parents of an Alternative, which are often from different comparison groups, are called its covering criteria.
Applying these definitions to the diagram, the four Criteria are children of the Goal, and the Goal is the parent of each of the four Criteria. Each Alternative is the child of its four covering criteria. There are two comparison groups: a group of four Criteria and a group of three Alternatives.
The design of any AHP hierarchy will depend not only on the nature of the problem at hand, but also on the knowledge, judgments, values, opinions, needs, wants, etc. of the participants in the process. Published descriptions of AHP applications often include diagrams and descriptions of their hierarchies. These have been collected and reprinted in at least one book.[22] More information about AHP hierarchies, including further reading and some complex real-world examples, can be found here.
As the AHP proceeds through its other steps, the hierarchy can be changed to accommodate newly-thought-of criteria or criteria not originally considered to be important; alternatives can also be added, deleted, or changed.[21]
A simple example
Because the AHP is a powerful tool for helping people with complex and important decisions, there really isn't a "simple" way of showing what it does. But it is possible to show how it works on a complicated decision problem that is familiar to most adults: the problem of choosing a car to buy. Since our goal is to show the use of a powerful tool, our example will dig deeper into the decision than most car real-world buyers are ever likely to. If you follow all the steps of the decision, you'll get a thorough introduction to the power of the Analytic Hierarchy Process.
In an AHP hierarchy for the simple case of buying a vehicle, the goal might be to choose the best car for the Jones family. After appropriate discussion and debate, the family might decide that Cost, Safety, Style, and Capacity are their criteria for making the decision. They might subdivide the Cost criterion into purchase price, fuel costs, maintenance costs, and resale value. They might separate Capacity into cargo capacity and passenger capacity. The family, which for personal reasons always buys Hondas, might decide to consider as alternatives the Accord Sedan, Accord Hybrid Sedan, Pilot SUV, CR-V SUV, Element SUV, and Odyssey Minivan.
The Jones' hierarchy could be diagrammed like this:
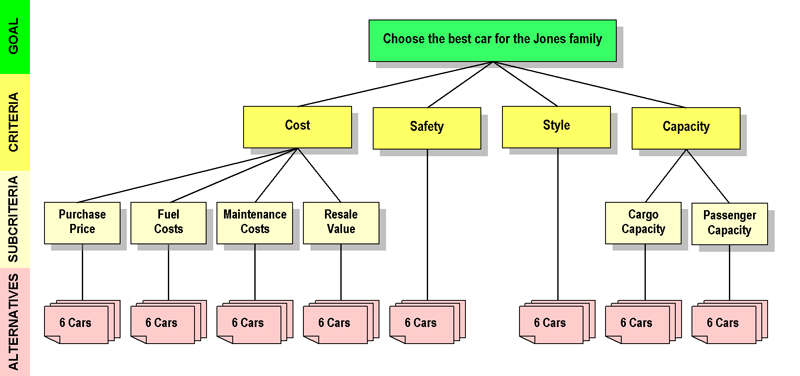
AHP hierarchy for the Jones family car buying decision. The Goal is green, the Criteria and Subcriteria are yellow, and the Alternatives are pink. All the alternatives (six different models of Hondas) are shown below the lowest level of each criterion. Later in the process, each alternative (each model) will be rated with respect to the criterion directly above it.

Alternatives for the Jones family car buying decision. To save space, we have represented them as stacks of papers.
Some simple terms apply to the boxes in the diagrams above. Each of the boxes is called a node. The boxes descending from any node are called its children. The node from which a child node descends is called its parent. Applying these definitions, the four Criteria are children of the Goal. The Goal is the parent of each of the four Criteria. Cargo Capacity and Passenger Capacity are the children of their parent, the Capacity criterion.
As they build their hierarchy, the Joneses should investigate the values or measurements of the different elements that make it up. If there are published safety ratings, for example, or manufacturer's specs for cargo capacity, they should be gathered as part of the process. This information will be needed later, when the criteria and alternatives are evaluated. Information about the Jones' alternatives, including color photos, can be found here.
Note that the measurements for some criteria, such as purchase price, can be stated with absolute certainty. Others, such as resale value, must be estimated, so must be stated with somewhat less confidence. Still others, such as style, are really in the eye of the beholder and are hard to state quantitatively at all. The AHP can accommodate all these types of criteria, even when they are present in a single problem.
Also note that the structure of the vehicle-buying hierarchy might be different for other families (ones who don't limit themselves to Hondas, or who care nothing about style, or who drive less than 5,000 miles a year, etc.). It would definitely be different for a 25-year-old playboy who doesn't care how much his cars cost, knows he will never wreck one, and is intensely interested in speed, handling, and the numerous aspects of style.[21]
Priorities
Once the hierarchy has been laid out, the participants use AHP to establish priorities, which are numbers associated with the nodes. By definition, the priority of the Goal is 1.000. The priorities of the Goal's children can vary in magnitude, but will always add up to 1.000. The priorities of the children of any of these children can also vary but will always add up to 1.000, as is the case for their own children, their children's children, and so on down the hierarchy.
This illustration shows some priorities for the Jones car buying hierarchy. We'll say more about them in a moment. For now, just observe that the priorities of the children of each parent node add up to 1.000, and that there are three such groups of children in the illustration. The alternatives also have priorities that follow these rules, but to keep our diagram simple, we haven't shown them here.
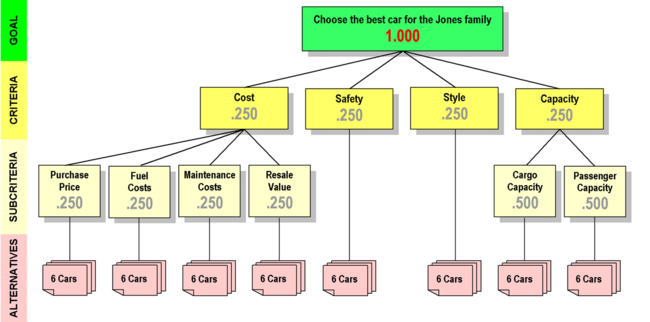
AHP hierarchy for the Jones family car buying decision, with some associated priorities.
If you understand what has been said so far, you will see that if we were to add a "Handling" criterion to this hierarchy, making five Criteria instead of four, the priority for each would be .200 instead of .250. You will also know that if the Safety criterion had three children, each of them would have a priority of .333.
In our example as it stands, the priorities within every group of child nodes are equal. In this situation, the priorities are called default priorities. Throughout this article, default priorities will be shown in gray. As the analytic hierarchy process continues, the priorities will change from their default values to reflect our judgments about the various items in each group.
The Goal's priority is a special case. Since it never changes from 1.000, we will always show it in red.
AHP priorities have another important feature. The priority of any child node represents its contribution to the priority of its parent. In the diagram above, Cost, Safety, Style and Capacity each contribute .250 of the 1.000 priority of the Goal. Cargo capacity and passenger capacity each contribute half of the priority belonging to the Capacity criterion. Working through the arithmetic, Passenger Capacity contributes .500 × .250 = .125 of the 1.000 priority of the Goal.
The meaning of priorities
As you may have guessed by now, the priorities indicate the relative weights given to the items in a given group of nodes. Depending on the problem at hand, "weight" can refer to importance, or preference, or likelihood, or whatever factor is being considered by the participants.
If all the priorities in a group of nodes are equal, each member of the group has equal weight. If one of the priorities is two times another, or three, (or whatever), that member has two, or three, (or whatever) times the weight of the other one. In our example, if we judge cargo capacity to be three times as important as passenger capacity, cargo capacity's new priority will be .750, and passenger capacity's priority will be .250. One will be three times the other, and they will still add up to 1.000. (Don't worry—the AHP software does all this arithmetic automatically.)
As we move ahead through the Analytical Hierarchy Process, information will be elicited from the participants and processed mathematically, changing the priorities throughout the hierarchy. This activity is somewhat complex, and the participants have many options on the road to completing it. The following material describes that activity for our Jones family car buying example. More information about hierarchies, including further reading and some complex real-world examples, can be found here.
Make pairwise comparisons[edit]
To incorporate their judgments about the various elements in the hierarchy, decision makers compare the elements two by two. How they are compared will be shown later on. Right now, let's see which elements are compared.
Our example will begin with the four Criteria in the second row of the hierarchy, though we could begin elsewhere if we wanted to.[23] The Criteria will be compared as to how important they are, to the decision makers, with respect to the Goal.
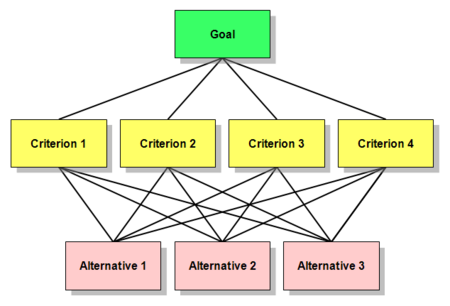
Each pair of items in this row will be compared; there are a total of six pairs (Cost/Safety, Cost/Style, Cost/Capacity, Safety/Style, Safety/Capacity, and Style/Capacity). You can use the diagram below to see these pairs more clearly.
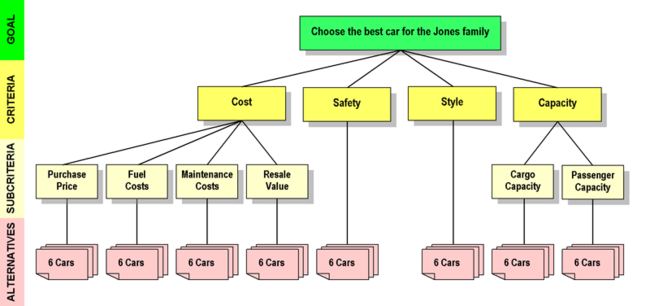
AHP hierarchy for the Jones family car buying decision. Can you see the six possible comparisons in the Criteria row?

Alternatives for the Jones family car buying decision. These six models will be pairwise compared with respect to each of the covering criteria—the items in the nodes immediately above each group of alternatives. In the example, these are Purchase Price, Fuel Costs, Maintenance Costs, Resale Value, Safety, Style, Cargo Capacity, and Passenger Capacity.
In the next row, there is a group of four subcriteria under the Cost criterion, and a group of two subcriteria under the Capacity criterion.
In the Cost subgroup, each pair of subcriteria will be compared regarding their importance with respect to the Cost criterion. (As always, their importance is judged by the decision makers.) Once again, there are a total of six pairs to compare (Purchase Price/Fuel Costs, Purchase Price/Maintenance Costs, Purchase Price/Resale Value, Fuel Costs/Maintenance Costs, Fuel Costs/Resale Value, and Maintenance Costs/Resale Value).
In the Capacity subgroup, there is only one pair of subcriteria. They will be compared as to how important they are with respect to the Capacity criterion.
Things change a bit when we get to the Alternatives row. Here, the cars in each group of alternatives will be compared pair-by-pair with respect to the covering criterion of the group. The covering criterion is the node directly above them in the hierarchy. What we are doing here is evaluating each of the models under consideration with respect to Purchase Price, then with respect to Fuel Costs, then Maintenance Costs, Resale Value, Safety, Style, Cargo Capacity, and Passenger Capacity. Because there are six cars in the group of alternatives, there will be fifteen comparisons for each of the eight covering criteria. That means we'll look at Purchase Price first.
When the pairwise comparisons are as numerous as those in our example, specialized AHP software can help in making them quickly and efficiently. We will assume that the Jones family has access to such software, and that it allows the opinions of various family members to be combined into an overall opinion for the group.
Comparing Criteria[edit]
The family's first pairwise comparison is Cost vs. Safety. They need to decide which of these is more important in choosing the best car for them all. This can be a difficult decision. On the one hand, "You can't put a price on safety. Nothing is more important than the life of a family member." But on the other hand, the family has a limited amount of money to spend, no member has ever had a major accident, and Hondas are known as very safe cars. In spite of the difficulty in comparing money to potential injury or death, the Jones family needs to determine its judgment about Cost vs. Safety in the car they are about to buy. They have to say which criterion is more important to them in reaching their goal, and how much more important it is (to them) than the other one. In making this judgment, they should remember that since the AHP is a flexible process, they can change their judgment later on.
You can imagine that there might be heated family discussion about Cost vs. Safety. It is the nature of the AHP to promote focused discussions about difficult aspects of the decisions to which it is applied. Such discussions encourage the communication of differences, which in turn encourages cooperation, compromise, and agreement among the members of the group.
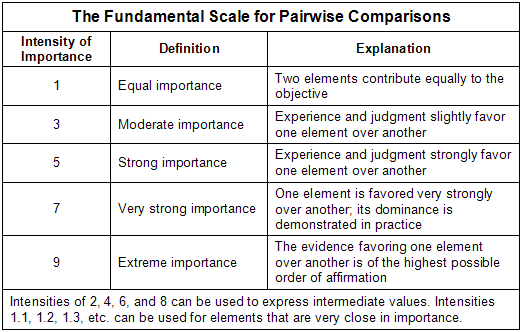
Let's say that the family decides that in this case, Cost is moderately more important to them than Safety. The software requires them to express this judgment by entering a number. They can use this table to determine it; in this case they would enter a 3 in favor of Cost:
Continuing our example, let's say they make the following judgments about all the comparisons of criteria, entering them into the software as numbers gotten from the table: as stated, Cost is moderately important (3) over Safety; also, Cost is very strongly important (7) over Style, and is moderately important (3) over Capacity. Safety is extremely more important (9) than Style, and of equal importance (1) to Capacity. Capacity is very strongly important (7) over Style.
We could show those judgments in a table like this:
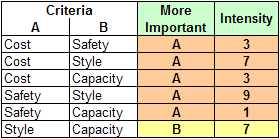
Judgments made by the Jones family and entered into the AHP software. Throughout this article, the family's judgments are shown with a green background. The orange and yellow colors show which alternative predominates.
The AHP software uses mathematical calculations to convert these judgments to priorities for each of the four criteria. The details of the calculations are beyond the scope of this article, but are readily available elsewhere.[24][2][25][26] The software also calculates a consistency ratio that expresses the internal consistency of the judgments that have been entered.
In this case the judgments showed acceptable consistency, and the software used the family's inputs to assign these new priorities to the criteria:
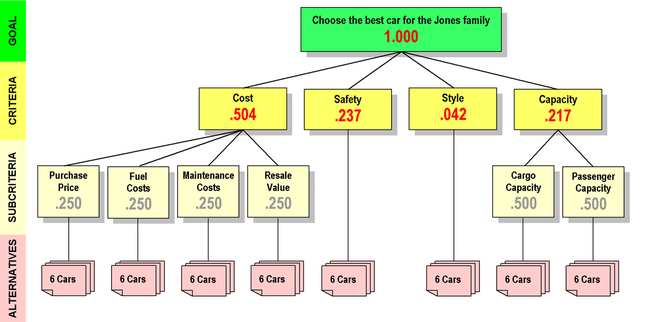
AHP hierarchy for the Jones family car buying decision. The Criteria have been pairwise compared, and their new priorities are shown. (Before the comparisons, each Criterion had a default priority of 0.250.) Note that the priorities still total 1.000, and the priorities for the subcriteria have not changed. The family has said that Cost is quite important to them, Style is relatively unimportant, and Safety and Capacity are each roughly half as important as Cost, with Safety having a slight edge over Capacity. Family members can look at these priorities and see how they feel about them. If they are uncomfortable about something, they can redo their pairwise comparisons.
You can duplicate this analysis at this online demonstration site; use the Line by Line Method by clicking its button, and don't forget to enter a negative number if the Criterion on the left is less important than the one on the right. If you are having trouble, click here for help. IMPORTANT: The demo site is designed for convenience, not accuracy. The priorities it returns may differ somewhat from those returned by rigorous AHP calculations. Nevertheless, it is useful in showing the mechanics of the pairwise comparison process. Once you are comfortable with the demo, you can experiment by entering your own judgments for the criteria in question. If your judgments are different from those of the Jones family, your priorities will possibly be quite different from theirs.[27]
Comparing Subcriteria[edit]
Look again at the above diagram and note that the Subcriteria still show their default priorities. This is because the decision makers haven't entered any judgments about them. So next on the family's agenda is to pairwise compare the four Subcriteria under Cost, then the two Subcriteria under Capacity. They will compare them following the same pattern as they did for the Criteria.
Let's say that after some discussion, the family agreed that under Cost, Purchase Price had a weight of 2 over Fuel Cost, 5 over Maintenance Cost, and 3 over Resale Value; Fuel Cost weighed 2 over Maintenance Cost and 2 over Resale Value; Resale Value weighed 2 over Maintenance Cost. Under Capacity, their single comparison weighed Passenger Capacity 5 over Cargo Capacity.
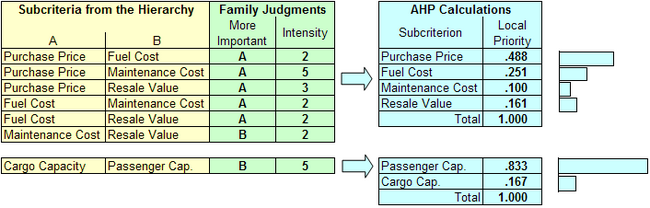
Pairwise comparisons of the Subcriteria, with the resulting LOCAL priorities. Yellow shows the pairs that are compared, green shows the family's judgments for each comparison, and blue shows the resulting priorities as calculated by the AHP software.
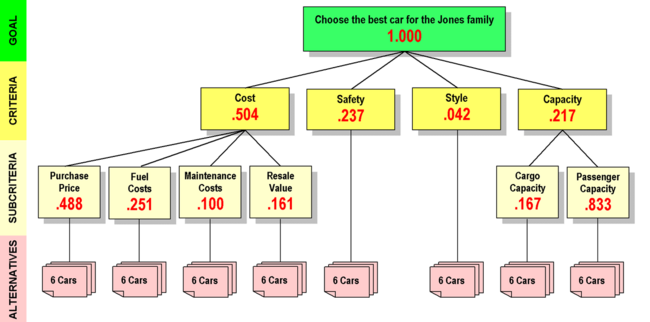
AHP hierarchy for the Jones family car buying decision, showing LOCAL priorities. The items in each group of Subcriteria have been pairwise compared, and their resulting priorities are shown. The priorities in each group total 1.000. These are called local priorities.
At this point, all the comparisons for Criteria and Subcriteria have been made, and the AHP software has derived the local priorities for each group at each level. One more step can be made here. We know how much the priority of each Criterion contributes to the priority of the Goal. Since we also know how much the priority of each Subcriterion contributes to the priority of its parent, we (and the AHP software) can calculate the global priority of each Subcriterion. That will show us the priority of each Subcriterion with respect to the Goal. The global priorities throughout the hierarchy will add up to 1.000, like this:
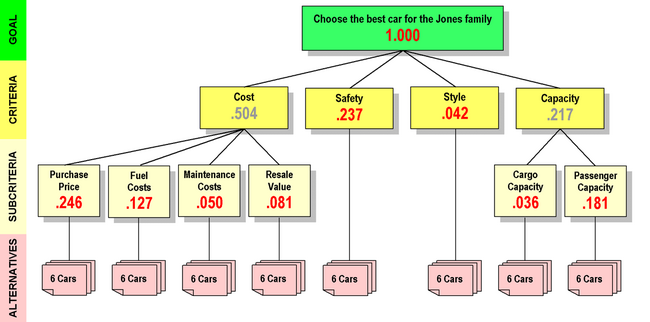
AHP hierarchy for the Jones family car buying decision, showing GLOBAL priorities. The priority of the Goal is 1.000, as always. The global priorities shown in red for the Criteria and Subcriteria also add up to 1.000. Each item with a red global priority contributes that amount to the priority of the Goal.
Based on the judgments entered by the family, the AHP has derived the priorities for the factors against which each of the six cars will be compared. The higher a factor's priority, the more important it is in achieving the goal of buying the best car for the family. In fact, the priorities are precisely related to the goal. A factor with priority 0.250 contributes 25% to reaching the goal. A factor with priority 0.050 contributes only 5%, and is therefore only one-fifth as important as a factor with priority 0.250.
The global priorities for the Criteria and Subcriteria are shown, from highest to lowest, in the table below:
| Factor | Global
Priority |
|---|---|
| Purchase Price | 0.246 |
| Safety | 0.237 |
| Passenger Capacity | 0.181 |
| Fuel Costs | 0.127 |
| Resale Value | 0.081 |
| Maintenance Costs | 0.050 |
| Style | 0.042 |
| Cargo Capacity | 0.036 |
| TOTAL | 1.000 |
The next step is to evaluate each of the cars with respect to these factors. In the technical language of AHP, we will pairwise compare the alternatives with respect to their covering criteria. Notice that the Cost and Capacity criteria will not be evaluated directly, but that their Subcriteria will be evaluated instead.
Comparing Alternatives[edit]
The family can evaluate alternatives against their covering criteria in any order they choose. In this case, they choose the order of decreasing priority of the covering criteria. That means Purchase Price first.
Purchase price[edit]
The family has established a budget of $25,000 for buying the new car, but they are willing to consider alternatives whose price exceeds their budget. To refresh your mind, here are the six cars they are considering—in AHP terminology, the six alternatives—along with their purchase prices:
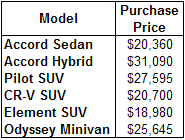
The Jones Family's alternatives, with purchase prices.
Knowing that they will have a lot of pairwise comparisons to make, the family prepared this worksheet to help them. It shows comparative information about the price and budget status of each pair of cars:
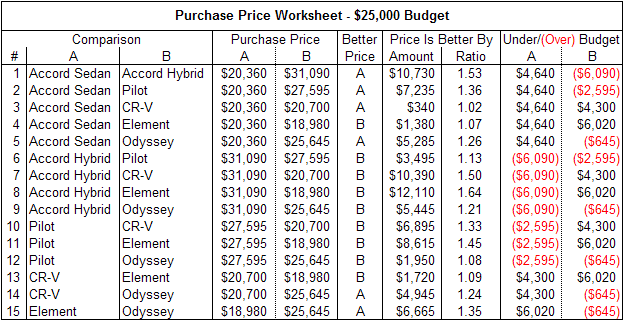
The Jones family's purchase price worksheet.
Now, what do they do?
First they might compare the purchase price of the Accord Sedan to that of the Accord Hybrid. If they stick purely to arithmetic, they could say that the Sedan is favored by 1.5, since the Hybrid's price is about 1.5 times that of the Sedan, and a lower price is better. They could follow that pattern through all 15 of the comparisons, and it would give a mathematically consistent set of comparisons.
But merely entering the numbers wouldn't take into account things like the $25,000 budget, or the value to the family of saving, say, $5,000 vs. $1,000 on a purchase. Things like that can be highly important in making decisions, and their importance can vary greatly with the situation and the people involved. Some families might never want to exceed their budget. Others might be willing to exceed it by a few dollars or a few percent, but very unwilling to go further. Still others might not care much if they spend double their budget on the car. Because the AHP allows decision makers to enter their judgments about the data, rather than just the data themselves, it can deal with all these situations and more.
Let's say that the Jones family is willing to exceed their budget by up to $1,000, but anything more is unacceptable. They "never say never," however—budget-busting cars will score as low as possible on purchase price, but won't be removed from the list of alternatives. And for cars priced under budget, a $1,000 difference in price doesn't matter much to the Joneses, but a $5,000 difference is strongly important, and a $10,000 difference is extreme. They might enter the following intensities into the AHP software (throughout this example, the judgments of decision makers are shaded in green):
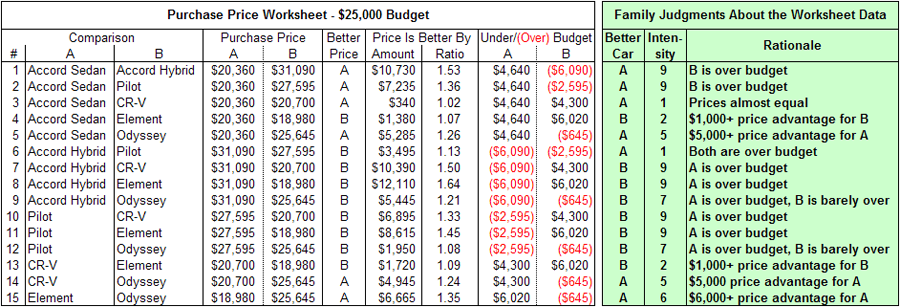
Purchase price judgments entered by the Jones family, with the rationale for their choices. From the Fundamental Scale, 1 expresses that A and B are equally preferred, 3 that A is moderately preferred to B, 5 that A is strongly preferred, 7 that A is very strongly preferred, and 9 that A is extremely preferred to B. Intensities 2, 4, 6, and 8 express intermediate values.
You can follow the family's thinking by looking at the rationale for each judgment. Whenever a car that is under budget is compared with one that is over budget by more than $1,000, the former is extremely preferred. For cars under budget, a $1,000 less expensive car is slightly preferred, a $5,000 one is strongly preferred, and a $6,000 one is even more strongly preferred. When both cars are well over budget (comparison #3), they are equally preferred, which is to say they are equally undesirable. Because budget status and absolute price difference are enough to make each comparison, the ratio of prices never enters into the judgments.
When the judgments shown above are entered, the AHP software returns the following priorities for the six alternatives with respect to Purchase Price:
| Alternative | Local
Priority |
Global
Priority |
|---|---|---|
| Element | 0.362 | 0.089 |
| Accord | 0.242 | 0.060 |
| CR-V | 0.242 | 0.060 |
| Odyssey | 0.100 | 0.025 |
| Pilot | 0.027 | 0.007 |
| Accord Hybrid | 0.027 | 0.007 |
| TOTAL | 1.000 | 0.246 |
The local priorities show how much the purchase price of each model contributes to the subcriterion of Purchase Price. The global priorities show how much the purchase price of each model contributes to the overall goal of choosing the best car for the Jones family.
Safety[edit]
Comparing the alternatives on the basis of Safety is much less objective than comparing them on Purchase Price. Purchase prices are measured in dollars and can be determined to the penny. People can easily agree on the meaning of a $20,360 purchase price, and can rationally compare it to all the other prices, using methods and calculations that are understood and accepted by all.
But "safety" eludes our efforts even to define it in an objective way. Not only that, but the objective measurements of safety are limited and not readily comparable from car to car.
The government conducts objective crash tests, but they are incomplete measures of the "safety" of a given car. Also, the crash tests only compare the members of a single class of cars, such as Midsize Cars or Minivans. Is a midsize car with 100% 5-star safety ratings equally as safe as a minivan with the same ratings? It's not exactly clear. And when evaluating minivans that have 5-star ratings in all categories but one, who can say if the one with four stars for "Frontal Impact, Driver's Side" is safer than the one whose four stars are in "Side Impact, Rear Occupant?" There's really no way to tell.
In spite of these difficulties, the AHP provides a rational way to evaluate the relative safety of different cars.
Let's assume that the Jones family has researched the Safety of the six Hondas they are considering. They will have found that all of them are among the safest cars on the road. All six are "Top Safety Picks" of the IIHS safety standards organization. All of them do very well in the crash testing programs of the National Highway Traffic Safety Administration. But there are differences between them, and the family wants to factor the differences into their decision. "Your car can never be too safe."
The worksheet below includes the data that the family has decided to evaluate. They believe that a heavier car is a safer car, so they've documented the curb weights of their alternatives. They have investigated the results of government crash tests, and they've summarized the results on the worksheet:
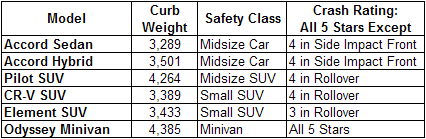
Safety data to be evaluated by the Jones family. Curb Weight is from manufacturer's literature. Crash Ratings are from NHTSA and are given for various classes of vehicle. For each class, they include Frontal Impact, Driver's Side; Frontal Impact, Passenger's Side; Side Impact, Front Occupant; Side Impact, Rear Occupant; and Rollover Rating. Ratings are from one to five stars, with five stars being the best.
The family will consider everything in the worksheet as they compare their alternatives. They are not safety experts, but they can apply their life experience to making decisions about the safety ratings. They all feel safer when driving a car that is significantly heavier than another one. One family member has seen two gruesome rollover accidents, and is terrified of a vehicle rolling over with her inside. She insists that the family car has the highest possible Rollover Rating.
Here are the weights that the Jones family enters for the alternatives regarding Safety (throughout this example, orange shading is used for judgments where A is favored; yellow shading is used for B):
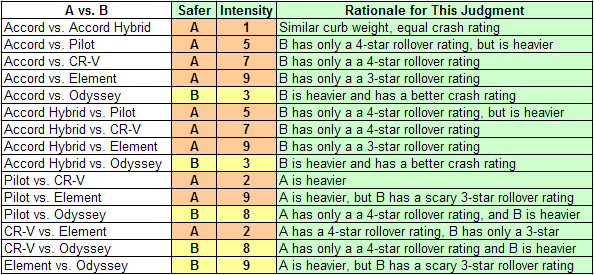
Safety judgments entered by the Jones family, with the intensity and rationale for each. From the Fundamental Scale, 1 expresses that A and B are equally preferred, 3 that the better of the pair is moderately preferred to the worse, 5 that the better is strongly preferred, 7 that the better is very strongly preferred, and 9 that the better is extremely preferred to the worse. Intensities 2, 4, 6, and 8 express intermediate values.
When the judgments shown above are entered, the AHP software returns the following priorities for the six alternatives with respect to Safety:
| Alternative | Local
Priority |
Global
Priority |
|---|---|---|
| Odyssey | 0.424 | 0.100 |
| Accord | 0.215 | 0.051 |
| Accord Hybrid | 0.215 | 0.051 |
| Pilot | 0.083 | 0.020 |
| CR-V | 0.038 | 0.009 |
| Element | 0.025 | 0.006 |
| TOTAL | 1.000 | 0.237 |
The local priorities show how much the safety of each model contributes to the Criterion of Safety. The global priorities show how much the Safety of each model contributes to the overall goal of choosing the best car for the Jones family.
Passenger capacity[edit]
This characteristic is easy to evaluate. The alternatives can carry either four or five or eight passengers. Here are the figures:
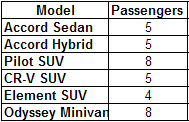
Passenger Capacity of the Jones family's alternatives.
The family has decided that four is barely enough, five is perfect for their needs, and eight is just a little bit better than five. Here are their judgments:
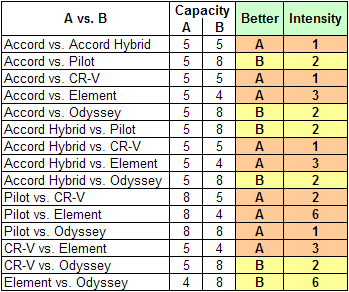
Passenger Capacity judgments entered by the Jones family. The rationale is that four passengers is barely enough, five is perfect for their needs, and eight is just a little bit better than five.
When the judgments shown above are entered, the AHP software returns the following priorities for the six alternatives with respect to Passenger Capacity:
| Alternative | Local
Priority |
Global
Priority |
|---|---|---|
| Pilot | 0.273 | 0.049 |
| Odyssey | 0.273 | 0.049 |
| Accord | 0.136 | 0.025 |
| Accord Hybrid | 0.136 | 0.025 |
| CR-V | 0.136 | 0.025 |
| Element | 0.046 | 0.008 |
| TOTAL | 1.000 | 0.181 |
The local priorities show how much the passenger capacity of each model contributes to the Subcriterion of Passenger Capacity. The global priorities show how much the passenger capacity of each model contributes to the overall goal of choosing the best car for the Jones family.
Fuel costs[edit]
After careful consideration, the Jones family believes that no matter which car they buy, they will drive it the same number of miles per year. In other words, there is nothing about any of the alternatives, including the price of fuel or the car's fuel consumption per mile, that would cause it to be driven more or fewer miles than any other alternative. They also believe that the government MPG rating is an accurate basis on which to compare the fuel consumption of the cars. Here is a worksheet showing the government MPG ratings of the Jones family alternatives:
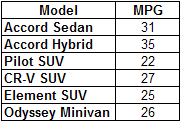
Fuel consumption figures for the Jones family's alternatives.
They believe, therefore, that the fuel cost of any alternative vs. any other depends exclusively on the MPG ratings of the two cars. So the pairwise judgments they enter for any two cars will be inversely proportional to their MPG ratings. In other words, if car A has exactly twice the MPG rating of car B, the Fuel Cost for car B will be exactly twice that of car A. This table shows the judgments they will enter for all the comparisons:
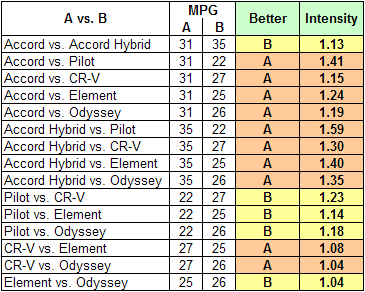
Fuel Cost judgments entered by the Jones family. Judgments are inversely proportional to the MPG ratings of the cars being compared.
When the judgments shown above are entered, the AHP software returns the following priorities for the six alternatives with respect to Fuel Cost:
| Alternative | Local
Priority |
Global
Priority |
|---|---|---|
| Accord Hybrid | 0.212 | 0.027 |
| Accord | 0.188 | 0.024 |
| CR-V | 0.160 | 0.020 |
| Odyssey | 0.156 | 0.020 |
| Element | 0.151 | 0.019 |
| Pilot | 0.133 | 0.017 |
| TOTAL | 1.000 | 0.127 |
The local priorities show how much the fuel cost of each model contributes to the subcriterion of Fuel Costs. The global priorities show how much the fuel cost of each model contributes to the overall goal of choosing the best car for the Jones family.
Resale Value[edit]
When the family researched Resale Value, they learned that lending institutions keep statistics on the market value of different models after various time periods. These estimated "residual values" are used for leasing, and are typically based on a limit of 12,000 miles driven per year. Actual residual values depend on the condition of the car, and can vary with market conditions.
The Joneses are going to buy their car, not lease it, and they expect to drive it more than 12,000 miles per year, but they agree among themselves that the leasing figures are a good basis on which to compare the alternatives under consideration. Their bank gave them this table showing the residual value of each alternative after four years and 48,000 miles:
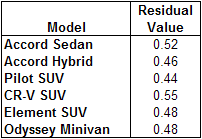
Four-year residual values. A value of 0.52 means that this model is worth 52% of its original price.
As they look at the table of residual values, they see that the residual value of a CR-V is 25% higher than that of a Pilot (0.55 is 125% of 0.44). They reason that such a greatly higher residual value is an indication of a better or more desirable car, so they want to place a premium on cars with relatively high residual value. After some thought and discussion, they decide that, when comparing residual values, they want to look at the higher one as a percentage of the lower, and assign their intensities on that basis. Where one model has a residual value that is less than 105% of another, they consider the residual values as equal for all practical purposes. Where one model has a residual value that is 125% of the residual value of another, they consider the former model as quite strongly more important, desirable, valuable, etc., as indicated by its much higher resale value. With a bit more thought and discussion, they decide to make their judgments on this basis:

The Jones rationale for comparing residual values. It is based on the higher residual value as a percentage of the lower one.
They realize that not every family would do it this way, but this way seems best for them. This table shows the judgments they will enter for their Resale Value comparisons:
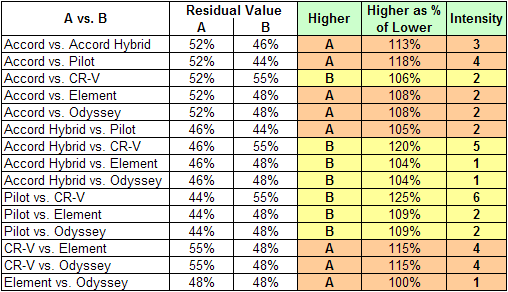
Resale Value comparisons entered by the Jones family. They are based on the rationale shown above.
When the judgments shown above are entered, the AHP software returns the following priorities for the six alternatives with respect to Resale Value:
| Alternative | Local
Priority |
Global
Priority |
|---|---|---|
| CR-V | 0.415 | 0.034 |
| Accord | 0.225 | 0.018 |
| Element | 0.105 | 0.009 |
| Odyssey | 0.105 | 0.009 |
| Accord Hybrid | 0.095 | 0.008 |
| Pilot | 0.055 | 0.004 |
| TOTAL | 1.000 | 0.081 |
The local priorities show how much the resale value of each model contributes to the Subcriterion of Resale Value. The global priorities show how much the resale value of each model contributes to the overall goal of choosing the best car for the Jones family.
Maintenance Costs[edit]
The Jones family researched maintenance costs for the cars under consideration, but they didn't find any hard figures. The closest they got was Consumer Reports magazine, which publishes 17 separate maintenance ratings for every car on the market. Their Hondas ranked very well, with all ratings "Much Better Than Average," except for a few on the Pilot and Odyssey. The Pilot got "Better Than Average" for its audio system and the user rating, and "Average" for body integrity. The Odyssey got "Better Than Average" for body hardware and power equipment, and "Average" for brakes, body integrity, and user rating.
The Joneses also asked their favorite mechanic to evaluate the maintenance costs for their six cars. Using tire prices and mileage estimates, he came up with figures for tire costs over 60,000 miles of driving. He didn't have figures for brake costs, but he said they'd be about twice as much for the SUVs and minivans as they would for the sedans. He also cautioned them that the battery in the Accord Hybrid was an expensive repair item, and that the engine placement on the Odyssey made it a more expensive car to work on.
The family created this worksheet to keep track of all their information about maintenance costs:
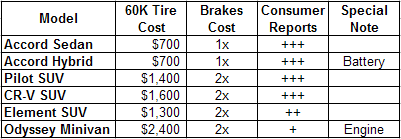
Jones family worksheet for Maintenance Costs. Plus signs indicate good maintenance history; the more plus signs, the lower the maintenance costs.
Even though every column on the worksheet contains a different type of information, the Joneses can use it to make reasonable, rational judgments about Maintenance Costs. Here are the judgments they will enter:
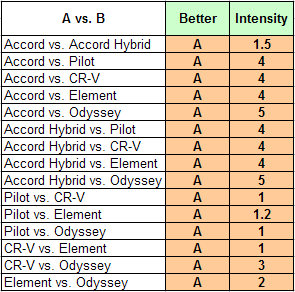
Maintenance Cost judgments entered by the Jones family. From the Fundamental Scale, 1 means that A and B are equally preferred, 3 that A is moderately preferred, and 5 that A is strongly preferred. Intermediate numbers express intermediate preferences.
When the judgments shown above are entered, the AHP software returns the following priorities for the six alternatives with respect to Maintenance Costs:
| Alternative | Local
Priority |
Global
Priority |
|---|---|---|
| Accord | 0.357 | 0.018 |
| Accord Hybrid | 0.312 | 0.016 |
| CR-V | 0.100 | 0.005 |
| Element | 0.089 | 0.004 |
| Pilot | 0.084 | 0.004 |
| Odyssey | 0.058 | 0.003 |
| TOTAL | 1.000 | 0.050 |
The local priorities show how much the projected maintenance cost of each model contributes to the subcriterion of Maintenance Costs. The global priorities show how much the maintenance cost of each model contributes to the overall goal of choosing the best car for the Jones family.
Style[edit]
The family decided that Style is important to them, but how can they determine the "style" of each of the six alternatives? "Style" is a pretty subjective concept—it can truly be said that "style is in the eye of the beholder." Yet through the method of pairwise comparison, the AHP gives the Jones family a way to evaluate the "style" of the cars they are considering.
Honda's web site provides photos of each of the alternatives. It also has videos, commercials, rotatable 360° views, color chips, and more, all available to help family members evaluate the Style of each car. The family can compare their alternatives two-by-two on Style, using the tools on the web site to help them make their judgments. They did just that, and here is the record of their judgments:
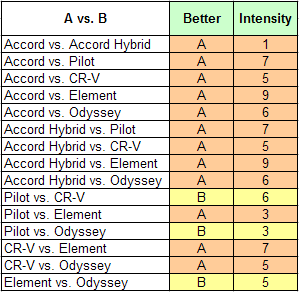
Style judgments entered by the Jones family. The family looked at each pair of cars as shown in detail on a web site, decided which of the two they preferred, then entered the intensity of their preference according to the Fundamental Scale.
When the judgments shown above are entered, the AHP software returns the following local priorities for the six alternatives with respect to Style:
| Alternative | Local
Priority |
Global
Priority |
|---|---|---|
| Accord | 0.346 | 0.015 |
| Accord Hybrid | 0.346 | 0.015 |
| CR-V | 0.160 | 0.007 |
| Odyssey | 0.078 | 0.003 |
| Pilot | 0.045 | 0.002 |
| Element | 0.025 | 0.001 |
| TOTAL | 1.000 | 0.042 |
The local priorities show how much the style of each model contributes to the Style Criterion. The global priorities show how much the Style of each model contributes to the overall goal of choosing the best car for the Jones family.
Cargo Capacity[edit]
The Cargo Capacity of each alternative, measured in cubic feet, is listed in the manufacturer's specifications for each vehicle. The Joneses don't really know how it is calculated, but they trust that it's a good indication of how much cargo can be packed into a vehicle. This worksheet shows the cargo capacities of the Jones' alternatives:
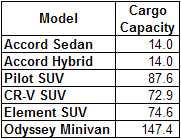
Cargo Capacity of the Jones' alternatives.
Cargo capacities for the alternatives vary from 14 to 148 cubic feet. If they wanted to, the Jones family could enter these capacities directly into the AHP software. But that would mean that, when considering Cargo Capacity, a car with 148 cu. ft. of it would be over ten times as desirable as one with only 14. Given the car's use as a family vehicle, that doesn't seem quite right. So the family looks at the available capacities and determines that a 14 cu. ft. trunk is perfectly fine for their needs, that something about five times larger is slightly better, and that something about ten times larger is moderately so. These judgments correspond to values of 1, 2, and 3 on the AHP's Fundamental Scale.
Here are the judgments they would enter into the AHP software:
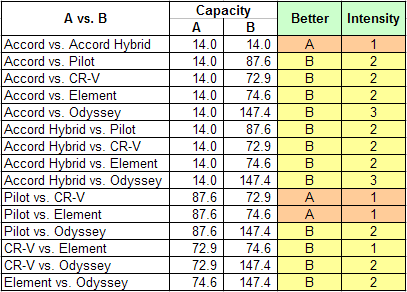
Cargo Capacity judgments entered by the Jones family. The rationale is that 14 cubic feet is totally satisfactory, five times that much (70 cu. ft.) is slightly better, and ten times that much (140 cu. ft.) is moderately better than 14.
When the judgments shown above are entered, the AHP software returns the following local priorities for the six alternatives with respect to Cargo Capacity:
| Alternative | Local
Priority |
Global
Priority |
|---|---|---|
| Odyssey | 0.310 | 0.011 |
| Pilot | 0.170 | 0.006 |
| CR-V | 0.170 | 0.006 |
| Element | 0.170 | 0.006 |
| Accord | 0.090 | 0.003 |
| Accord Hybrid | 0.090 | 0.003 |
| TOTAL | 1.000 | 0.036 |
The local priorities show how much the cargo capacity of each model contributes to the subcriterion of Cargo Capacity. The global priorities show how much the cargo capacity of each model contributes to the overall goal of choosing the best car for the Jones family.
Make the decision[edit]
In the end, the AHP software arranges and totals the global priorities for each of the alternatives. Their grand total is 1.000, which is identical to the priority of the goal. Each alternative has a global priority corresponding to its "fit" to all the family's judgments about all those aspects of Cost, Safety, Style and Capacity. Here is a summary of the global priorities of the alternatives:
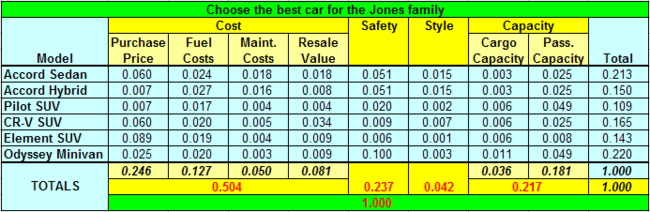
Global priorities for the Jones family car buying decision. Note that the priorities for each group of children total that of their parent.
The Odyssey Minivan, with a global priority of 0.220, is the alternative that contributes the most to the goal of choosing the best car for the Jones family. The Accord Sedan is a close second, with a priority of 0.213. The other models have considerably less priority than those two. In descending order, they are CR-V SUV, Accord Hybrid, Element SUV, and Pilot SUV.
The Analytic Hierarchy Process has shown the Joneses that the Odyssey Minivan best satisfies all their criteria and judgments, followed closely by the Accord Sedan. The other alternatives fall significantly short of meeting their criteria. The family's next step is up to them. They might just go out and buy an Odyssey, or they might use the AHP or other means to refine their decision between the Odyssey and the Accord Sedan.
Criticisms[edit]
Although the Analytic Hierarchy Process has been the subject of many research papers and the general consensus is that the technique is both valid and useful, there are critics of the method.[5] Their criticisms have included: A) since there is no theoretical basis for constructing hierarchies, AHP users can construct different hierarchies for identical decision situations, possibly producing different solutions, B) AHP rankings are claimed to be arbitrary because they are based on subjective opinions using a ratio scale, a situation which can produce "rank reversal," C) there are said to be flaws in the methods of combining individual weights into composite weights, and D) the process has no sound underlying statistical theory. [3]
New methodologies started being develop to tackle some of the criticisms against AHP. The main known ones are the PROMETHEE[28] methodology and also the [MAUT] methodology.
References[edit]
- ↑ Saaty, Thomas L. (2008-06). "Relative Measurement and its Generalization in Decision Making: Why Pairwise Comparisons are Central in Mathematics for the Measurement of Intangible Factors - The Analytic Hierarchy/Network Process". RACSAM (Review of the Royal Spanish Academy of Sciences, Series A, Mathematics) 102 (2): 251-318. Retrieved on 2008-12-22.
- ↑ 2.0 2.1 2.2 Bhushan, Navneet; Kanwal Rai (January 2004). Strategic Decision Making: Applying the Analytic Hierarchy Process. London: Springer-Verlag. ISBN 1-8523375-6-7.
- ↑ 3.0 3.1 3.2 de Steiguer, J.E. (October 2003), The Analytic Hierarchy Process as a Means for Integrated Watershed Management, in Renard, Kenneth G., First Interagency Conference on Research on the Watersheds, Benson, Arizona: U.S. Department of Agriculture, Agricultural Research Service, at 736–740
- ↑ Berrittella, M. (January, 2007), An Analytic Hierarchy Process for the Evaluation of Transport Policies to Reduce Climate Change Impacts, Fondazione Eni Enrico Mattei (Milano)
- ↑ 5.0 5.1 McCaffrey, James (June 2005). "Test Run: The Analytic Hierarchy Process". MSDN Magazine. Retrieved on 2007-08-21.
- ↑ Grandzol, John R. (August 2005). "Improving the Faculty Selection Process in Higher Education: A Case for the Analytic Hierarchy Process" (PDF). IR Applications 6. Retrieved on 2007-08-21.
- ↑ Atthirawong, Walailak (September, 2002), An Application of the Analytical Hierarchy Process to International Location Decision-Making, in Gregory, Mike, Proceedings of The 7th Annual Cambridge International Manufacturing Symposium: Restructuring Global Manufacturing, Cambridge, England: University of Cambridge, at 1–18
- ↑ Dey, Prasanta Kumar (November 2003). "Analytic Hierarchy Process Analyzes Risk of Operating Cross-Country Petroleum Pipelines in India". Natural Hazards Review 4 (4): 213–221. DOI:10.1061/(ASCE)1527-6988(2003)4:4(213). Retrieved on 2007-08-20. Research Blogging.
- ↑ Lippert, Barbara C.; Stephen F. Weber (October 1995). "HIST 1.0; Decision Support Software for Rating Buildings by Historic Significance" (PDF). National Institute of Standards and Technology, NISTIR 5683. Retrieved on 2007-08-20.
- ↑ Larson, Charles D. (January, 2007), Application of the Analytic Hierarchy Process to Select Project Scope for Videologging and Pavement Condition Data Collection, 86th Annual Meeting Compendium of Papers CD-ROM, Transportation Research Board of the National Academies
- ↑ Participant Names and Papers, ISAHP 2005, Honolulu, Hawaii (July 2005). Retrieved on 2007-08-22.
- ↑ 12.0 12.1 Sun, Hongkai (July, 2005), AHP in China, in Levy, Jason, Proceedings of the 8th International Symposium on the Analytic Hierarchy Process, Honolulu, Hawaii
- ↑ List of Expert Choice education clients. Retrieved on 2007-08-23.
- ↑ Drake, P.R. (1998). "Using the Analytic Hierarchy Process in Engineering Education" (PDF). International Journal of Engineering Education 14 (3): 191–196. Retrieved on 2007-08-20.
- ↑ Bodin, Lawrence; Saul I. Gass (January 2004). "Exercises for Teaching the Analytic Hierarchy Process" (Template:Dead link – Scholar search). INFORMS Transactions on Education 4 (2). Retrieved on 2007-08-20.
- ↑ Hallowell, David L. (January 2005). "Analytical Hierarchy Process (AHP) – Getting Oriented". iSixSigma.com. Retrieved on 2007-08-21.
- ↑ "Analytic Hierarchy Process (AHP)". QFD Institute. Retrieved on 2007-08-21.
- ↑ "Analytical Hierarchy Process: Overview". TheQualityPortal.com. Retrieved on 2007-08-21.
- ↑ Decision Lens web site. Retrieved on 2008-07-27.
- ↑ Expert Choice web site. Retrieved on 2008-07-27.
- ↑ 21.0 21.1 21.2 21.3 Saaty, Thomas L. (1999-05-01). Decision Making for Leaders: The Analytic Hierarchy Process for Decisions in a Complex World. Pittsburgh, Pennsylvania: RWS Publications. ISBN 0-9620317-8-X. (This book is the primary source for the sections in which it is cited.)
- ↑ Saaty, Thomas L.; Ernest H. Forman (1992). The Hierarchon: A Dictionary of Hierarchies. Pittsburgh, Pennsylvania: RWS Publications. ISBN 0-9620317-5-5. 496 pages, spiral bound. Each entry includes a description and diagram of an AHP model; the models are grouped in categories: educational, government/public policy, government public/strategy, health military, non-profit, personal, planning, political, etc.
- ↑ Many experts recommend evaluating the hierarchy from the bottom up, starting with each of the alternatives. The "top down" approach is simpler to explain, so we've chosen to use it in our example.
- ↑ Saaty, Thomas L. (2001). Fundamentals of Decision Making and Priority Theory. Pittsburgh, Pennsylvania: RWS Publications. ISBN 0-9620317-6-3.
- ↑ Trick, Michael A. (1996-11-23). Analytic Hierarchy Process. Class Notes. Carnegie Mellon University Tepper School of Business. Retrieved on 2008-03-02.
- ↑ Meixner, Oliver; Reiner Haas (2002). Computergestützte Entscheidungs-findung: Expert Choice und AHP – innovative Werkzeuge zur Lösung komplexer Probleme (in German). Frankfurt/Wien: Redline Wirtschaft bei Ueberreuter. ISBN 3-8323-0909-8.
- ↑ Note that the demo site expresses priorities in percentages rather than decimal fractions as we do. It also uses different numbers to represent the verbal descriptions presented here. It's only a demo, but you should use our numbers, not theirs, and you should convert the percentages to decimal fractions. IMPORTANT: The demo site is designed for convenience, not accuracy. The priorities it returns may be significantly different from those returned by rigorous AHP calculations.
- ↑ PROMETHEE-GAIA. B. Mareschal. Retrieved on 19 October 2013.
- ↑ 29. About PROMETHEE methodology [1]
- ↑ 30. D-Sight, company specialist on decision-making software based on PROMETHEE method.
- ↑ 31. About MAUT methodology [2]
 KSF
KSF