Cent (music)

	Main Article	Discussion	Related Articles  [?]	Bibliography  [?]	External Links  [?]	Citable Version  [?]
	This editable Main Article is under development and subject to a disclaimer. [edit intro]

The cent is a logarithmic measure of a musical interval introduced by Alexander Ellis. A cent is the logarithmic division of the equitempered semitone into 100 equal parts.

Formula[edit]

In terms of a formula, the separation or interval between two frequencies ƒ₁ and ƒ₂ in cents is determined as:

${\displaystyle c=1200\log _{2}\left({\frac {f_{1}}{f_{2}}}\right)\ .}$

Consequently, two frequencies ƒ₁ and ƒ₂ separated by an interval of 1 cent are in the ratio:

${\displaystyle {\frac {f_{1}}{f_{2}}}=2^{1/1200}\approx 1.005777895\ ,}$

that is, by a ratio given by the 1200th root of 2.

Background[edit]

The cent appears in an article Alexander Ellis published in 1885^[1] and also in an appendix he added to his translation of Herman von Helmholtz's Die Lehre von den Tonempfindungen published in translation as On the Sensation of Tone As a Physiological Basis for the Theory of Music,^[2] and also as On the sensations of tone.^[3]

(PD) Image: John R Brews
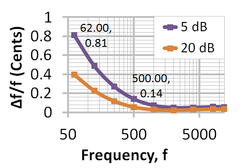
Audible difference in frequency Δƒ/ƒ at two sound levels heard in rapid succession vs. frequency ƒ.^[4]

(PD) Image: John R Brews
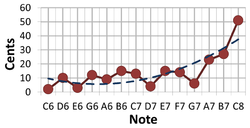
Average error of nine flutists in playing a note of specified pitch after listening to a pitch A4 = 442 Hz from a piano.^[5]

Sensitivity of the ear[edit]

See also: Music perception

According to Ellis, when two notes are played together, a difference of 2 cents is noticeable, and a difference of 5 cents is heard as out of tune.^[1]

The figure at right indicates a smaller sound level difference is audible when the sounds are louder, and smaller differences also are audible at higher frequencies.^[4] The ability to distinguish pitches is extremely variable among listeners, increases with intensity, increases with the abruptness in change of tone, improves with the richness of timbre,^[4] and varies with the shape of the envelope of the waveform that turns the tones on and off.^[6]

Recent observations suggest errors of 5-15 cents when playing a specific pitch are common, with errors of 20-50 cents for pitches above A7 (the 7th octave, 3 octaves above the octave containing middle C). (See figure at right.) The increased error at higher pitch was traced to a systematic error in the response of auditory nerves in the ear.^[5]

References[edit]