Point (geometry)

	Main Article	Discussion	Related Articles  [?]	Bibliography  [?]	External Links  [?]	Citable Version  [?]
	This editable Main Article is under development and subject to a disclaimer. [edit intro]

Diagram of a point (in blue) called A (with its label in black)

Diagram of a point using an alternative "circle" notation

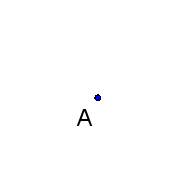
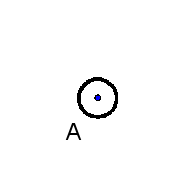
A point is a mathematical object in geometry which has a position but neither length nor breadth nor depth. A point is made up of no other parts. The extremities of a line segment are points. Geometric objects, such as lines, planes, line segments, triangles, circles, disks, spheres, balls, cubes etc., are often (but not always) treated as sets of points.

In Euclidean geometry:

A line is made up of an infinite number of points. Any line can be completely defined by two distinct points. Any plane can be completely defined by three distinct points that are not all part of the same line. Any two lines that lay on a single plane and are not parallel (nor coincide) intersect at a single point. Three planes typically intersect at a single point (though in special cases their intersection can be empty, a line, or a plane).

Beyond mathematics[edit]

(CC) Image: M.V. Jantzen
Stubby marker, a high-accuracy geodetic control mark.

In geodesy, a point on the Earth is marked by a so-called geodetic control mark. The distance between such points can be determined with the accuracy about 10^-7 of the distance (say, 100 km plus/minus 10 mm).

Individual atoms are probably the smallest (about 10^–10 m) marks on a surface that persist during a macroscopic time (hours, days). See the world’s smallest corporate logo.