Right-hand rule

	Main Article	Discussion	Related Articles  [?]	Bibliography  [?]	External Links  [?]	Citable Version  [?]
	This editable Main Article is under development and subject to a disclaimer. [edit intro]

CC Photo
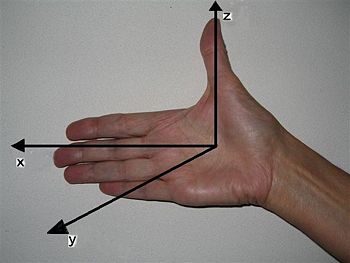
Right-hand rule. Move open palm of right hand from x  to y, then thumb is direction of z.

The right-hand rule relates a rotation to a vector perpendicular to the plane of rotation.

Cross product[edit]

The right-hand rule appears in the cross product,

${\displaystyle \mathbf {e} _{z}=\mathbf {e} _{x}\times \mathbf {e} _{y}.}$

The direction of the unit vector e_z given as the cross product of unit vectors along the x- and y-axis is given by the right-hand rule, see photograph.^[1]

The case depicted here employs the x- , y- , and z-axis, which normally are orthogonal to each other. However, the rule works for any two straight lines in the xy-plane at some angle α, as long as 0° < α ≤ 180°. If the vector e₁ points along one line and it can be rotated in the sense of the fingers of the right hand to align with a vector e₂ along the other line, then the direction of the cross-product e₁×e₂ always is in the z-direction perpendicular to the xy-plane and in the direction of the thumb.

Torque[edit]

(PD) Image: John R. Brews
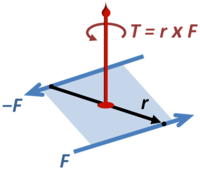
Torque vector T representing a force couple.

A torque is generated by a pair of equal and opposite forces in the same plane, called a force couple. If the right-hand is arranged so the fingers circle in the direction of the couple, the thumb points in the direction of the vector normal to their plane representing the torque, and the magnitude of the vector is taken as the magnitude of the couple. For example, if the forces of the couple are F and −F, and the vector r in their plane separates the two, the couple exerts a torque T = r × F provided r is taken in the direction that makes this cross product point in the same direction as the torque.^[2]

Angular momentum[edit]

The angular momentum of a body is related to its motion about a circular path or in turning on its own axis. If the right hand is arranged so the fingers point in the direction of motion, or rotation, the thumb points in the direction of the vector representing the angular momentum. It is normal to the plane of rotation and its magnitude is taken to be that of the angular momentum.^[3]

Notes[edit]