Square of opposition
 From Citizendium - Reading time: 5 min
From Citizendium - Reading time: 5 min
In Aristotelian logic, the square of opposition is a diagram representing the different ways in which each of the four propositions of the system are logically related ('opposed') to each of the others.
Summary[edit]
In traditional logic, a proposition (Latin: propositio) is a spoken assertion (oratio enunciativa), not the meaning of an assertion, as in modern philosophy of language and logic. A categorical proposition is a simple proposition containing two terms, subject and predicate, in which the predicate is either asserted or denied of the subject.
Every categorical proposition can be reduced to one of four logical forms. These are:
- The so-called 'A' proposition, the universal affirmative (universalis affirmativa), whose form in Latin is 'omnis S est P', usually translated as 'every S is P'.
- The 'E' proposition, the universal negative (universalis negativa), Latin form 'nullus S est P', usually translated as 'no S is P'.
- The 'I' proposition, the particular affirmative (particularis affirmativa), Latin 'quoddam S est P', usually translated as 'some S is P'.
- The 'O' proposition, the particular negative (particularis negativa), Latin 'quoddam S non est P', usually translated as 'some S is not P'.
In tabular form:
| Name | Symbol | Latin | English | SSF |
|---|---|---|---|---|
| Universal affirmative | A | Omnis S est P | Every S is P | All S is P |
| Universal negative | E | Nullus S est P | No S is P | All S is not P |
| Particular affirmative | I | Quoddam S est P | Some S is P | Some S is P |
| Particular negative | O | Quoddam S non est P | Some S is not P | Some S is not P |
Aristotle states (in chapters six and seven of the Perihermaneias (Latin De Interpretatione, English 'On Exposition'), that there are certain logical relationships between these four kinds of proposition. He says that to every affirmation there corresponds exactly one negation, and that every affirmation and its negation are 'opposed' such that always one of them must be true, and the other false. A pair of affirmative and negative statements he calls a 'contradiction' (in medieval Latin, contradictio). Examples of contradictories are 'every man is white' and 'not every man is white', 'no man is white' and 'some man is white'.
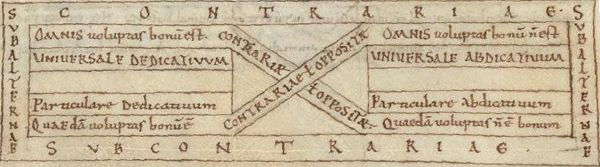
'Contrary' (medieval: contrariae) statements, are such that both cannot at the same time be true. Examples of these are the universal affirmative 'every man is white', and the universal negative 'no man is white'. These cannot be true at the same time. However, these are not contradictories because both of them may be false. For example, it is false that every man is honest, since some men are not honest. Yet it is also false that no man is honest, since there are some honest men.
Since every statement has a contradictory opposite, and since a contradictory is true when its opposite is false, it follows that the opposites of contraries (which the medievals called subcontraries, subcontrariae) can both be true, but they cannot both be false. Since subcontraries are negations of universal statements, they were called 'particular' statements by the medieval logicians.
A further logical relationship implied by this, though not mentioned explicitly by Aristotle, is subalternation (subalternatio). This is a relation between a particular statement and a universal statement such that the particular is implied by the other. For example, if 'every man is white' is true, its contrary 'no man is white' is false. Therefore the contradictory 'some man is white' is true. Similarly the universal 'no man is white' implies the particular 'not every man is white'.
In summary:
- Universal statements are contraries: 'every man is just' and 'no man is just' cannot be true together, although one may be true and the other false, and also both may be false (if at least one man is just, and at least one man is not just).
- Particular statements are subcontraries. 'Some man is just' and 'some man is not just' cannot be false together
- The universal affirmative and the particular affirmative are subalternates, because in Aristotelian semantics 'every A is B' implies 'some A is B'. Note that modern formal interpretations of English sentences interpret 'every A is B' as 'for any x, x is A implies x is B', which does not imply 'some x is A'. This is a matter of semantic interpretation, however, and does not mean, as is sometimes claimed, that Aristotelian logic is 'wrong'.
- The universal affirmative and the particular negative are contradictories. If some A is not B, not every A is B. Conversely, though this is not the case in modern semantics, it was thought that if every A is not B, some A is not B. This interpretation has caused difficulties (see below). While Aristotle's Greek does not represent the particular negative as 'some A is not B', but as 'not every A is B', Boethius in his commentary on the Perihermaneias, renders the particular negative as 'quoddam A non est B', literally 'a certain A is not a B', and in all medieval writing on logic it is customary to represent the particular proposition in this way.
These relationships became the basis of a diagram originating with Boethius and used by medieval logicians to classify the logical relationships. The propositions are placed in the four corners of a square, and the relations represented as lines drawn between them, whence the name 'The Square of Opposition'.
The problem of existential import[edit]
Subcontraries, which medieval logicians represented in the form 'quoddam A est B' (some particular A is B) and 'quoddam A non est B' (some particular A is not B) cannot both be false, since their universal contradictory statements (every A is B / no A is B) cannot both be true. This leads to a difficulty that was first identified by Peter Abelard. 'Some A is B' seems to imply 'something is A'. For example 'Some man is white' seems to imply that at least one thing is a man, namely the man who has to be white if 'some man is white' is true. But 'some man is not white' also seems to imply that something is a man, namely the man who is not white if 'some man is not white' is true. But Aristotelian logic requires that necessarily one of these statements is true. Both cannot be false. Therefore (since both imply that something is a man) it follows that necessarily something is a man, i.e. men exist. But (as Abelard points out, in the Dialectica) surely men might not exist? [1]
- For with absolutely no man existing, neither the proposition 'every man is a man' is true nor 'some man is not a man'[2].
Abelard also points out that subcontraries containing subject terms denoting nothing, such as 'a man who is a stone', are both false.
- If 'every man who is a stone, is a stone' is true, also its conversion per accidens is true ('a certain stone is a man who is a stone'). But no stone is a man who is a stone, because neither this man nor that man &c is a stone. But also this 'a certain man who is a stone, is not a stone' is false by necessity, since it is impossible to suppose it is true. ([3]).
[in progress: Mill on the problem of existential import, Strawson's answer, Parson's answer]
References[edit]
- ↑ In his Dialectica, and in his commentary on the Perihermaneias
- ↑ Re enim hominis prorsus non existente neque ea vera est quae ait: omnis homo est homo, nec ea quae proponit: quidam homo non est homo
- ↑ Si enim vera est: Omnis homo qui lapis est, est lapis, et eius conversa per accidens vera est: Quidam lapis est homo qui est lapis. Sed nullus lapis est homo qui est lapis, quia neque hic neque ille etc. Sed et illam: Quidam homo qui est lapis, non est lapis, falsam esse necesse est, cum impossibile ponat
 KSF
KSF