EncycloReader

From Conservapedia - Reading time: 1 min

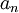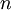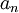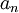In a metric space (X, d), a sequence $\text{[math]}$ in X is said to converge to a point $\text{[math]}$ if roughly speaking as $\text{[math]}$ goes to infinity $\text{[math]}$ gets closer and closer to $\text{[math]}$ and stays there. Rigorously, $\text{[math]}$ is said to converge to $\text{[math]}$ if for all 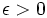$\text{[math]}$ there exists N such that for all n > N we have $\text{[math]}$ .

Similar definitions can be made for convergence of functions.

Licensed under CC BY-SA 3.0 | Source: https://www.conservapedia.com/Converge
13 views | Status: cached on April 11 2024 16:08:19
↧ Download this article as ZWI file