EncycloReader

From Conservapedia - Reading time: 2 min

A field is a commutative ring which contains a non-zero multiplicative identity and all non-zero elements have multiplicative inverses. Loosely, a field is a collection of entities with well-behaved and compatible addition and multiplication operations. A few examples serve to illustrate this point.

Examples[edit]

The rational numbers $\text{[math]}$ , with operations the usual addition and multiplication.
The real numbers $\text{[math]}$ , with operations the usual addition and multiplication.
The complex numbers $\text{[math]}$ , with operations the usual addition and multiplication.
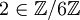The integers modulo $\text{[math]}$ (denoted $\text{[math]}$ ), where $\text{[math]}$ is prime. Here the operations are addition and multiplication modulo $\text{[math]}$ . Observe that if $\text{[math]}$ is not prime, then $\text{[math]}$ is not a field. For example, the element $\text{[math]}$ has no multiplicative inverse modulo 6! In this case, $\text{[math]}$ has only the structure of a ring.
The field $\text{[math]}$ of real numbers of the form $\text{[math]}$ , where both $\text{[math]}$ and $\text{[math]}$ are rational.
Finite fields: for each prime number $\text{[math]}$ and positive integer 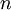$\text{[math]}$ , there is a unique (up to isomorphism) finite field of cardinality is $\text{[math]}$ . This field is of characteristic $\text{[math]}$ .
The set of meromorphic functions on a complex manifold, with pointwise addition and multiplication. For example, the set of meromorphic functions on $\text{[math]}$ or the unit disk $\text{[math]}$ .
The p-adic fields $\text{[math]}$ and $\text{[math]}$ , which play a prominent role in number theory.

The characteristic of a field must be either 0 or a prime number p. A field of characteristic 0 is necessarily infinite.

Fields play an important role in nearly every area of mathematics, and are one of the most basic objects studied by algebra. The study of the relationships between different fields, and in particular subfields of a given field, leads to the study of Galois theory, and makes possible the proof of Abel's theorem and was one of the motivations for the early study of fields and abstract algebra more generally.

Axioms[edit]

Technically, a field 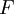$\text{[math]}$ is a set of elements endowed with two binary operations, $\text{[math]}$ and $\text{[math]}$ (with properties analogous to addition and multiplication, respectively), which obey the following axioms:

Addition axioms
1. Closure: If $\text{[math]}$ then $\text{[math]}$ .
2. Associativity: For $\text{[math]}$ , $\text{[math]}$ .
3. Commutativity: For $\text{[math]}$ $\text{[math]}$ .
4. Identity: There exists an element $\text{[math]}$ such that $\text{[math]}$ for all $\text{[math]}$ .
5. Inverse: For all $\text{[math]}$ there exists an element $\text{[math]}$ such that $\text{[math]}$ .
Multiplication axioms
1. Closure: If $\text{[math]}$ then $\text{[math]}$ .
2. Associativity: For $\text{[math]}$ , $\text{[math]}$ .
3. Commutativity: For $\text{[math]}$ , $\text{[math]}$ .
4. Identity: There exists an element $\text{[math]}$ such that $\text{[math]}$ for all $\text{[math]}$ .
5. Inverse: If $\text{[math]}$ and $\text{[math]}$ then there exists an element $\text{[math]}$ such that $\text{[math]}$ .
Distributivity: For $\text{[math]}$ , $\text{[math]}$ .