Table of Contents
  Encyclosphere.org ENCYCLOREADER
  supported by EncyclosphereKSF

System dynamics

From EduTechWiki - Reading time: 8 min

Introduction[edit | edit source]

System dynamics refers to a type of computer modeling and computer simulation created in the 1960s by Dr. Jay W. Forrester of the Massachusetts Institute of Technology. It originally was used in management and engineering, but is now used to model all sorts of simpler or complex systems. A well know example is the Club of Rome model World model (wikipedia) developed for the limits to growth report by Meadows et al. [1].

In the field of system dynamics, a system is defined as a collection of elements that continually interact over time to form a unified whole. The underlying relationships and connections between the components of a system is called the structure of the system. One familiar example of a system is an ecosystem. The structure of an ecosystem is defined by the interactions between animal populations, birth and death rates, quantities of food, and other variables specific to a particular ecosystem. The structure of the ecosystem includes the variables important in influencing the system.

The term dynamics refers to change over time. If something is dynamic, it is constantly changing. A dynamic system is therefore a system in which the variables interact to stimulate changes over time. System dynamics is a methodology used to understand how systems change over time. The way in which the elements or variables composing a system vary over time is referred to as the behavior of the system. In the ecosystem example, the behavior is described by the dynamics of population growth and decline. The behavior is due to the influences of food supply, predators, and environment, which are all elements of the system.

(The First Step, retrieved Feb 2019)

See also:

The language[edit | edit source]

The system dynamics group invented a way to represent differential equation in a way that is very accessible to novices. It is possible to create simple simulations without any understanding of the mathematics behind such models.

The first system created was called Dynamo. According to wikipedia, DYMAMO “is a historically important simulation language and accompanying graphical notation developed within the system dynamics analytical framework. It was originally for industrial dynamics but was soon extended to other applications, including population and resource studies and urban planning. DYNAMO was initially developed under the direction of Jay Wright Forrester in the late 1950s, by Dr. Phyllis Fox Alexander L. Pugh III, Grace Duren, and others at the M.I.T. Computation Center.” Both commercial (e.g. STELLA) and non-commercial derivatives came into existence later. A system can be described with five different elements.

A System dynamics model includes three to five different types of nodes (stocks, flows, convertors, constants) and two types of connectors. Marting in his 1997 tutorial [2] defines the following system dynamics language elements (slightly modified by us):

Stock —a generic symbol for anything that accumulates or drains. For example, water accumulates in your bathtub. At any point in time, the amount of water in the bathtub reflects the accumulation of what has flowed in from the faucet, minus what has flowed out down the drain. The amount of water in the bathtub is the stock of water.

Flow — the rate of change of a stock, i.e. what comes in and goes out. In the bathtub example, the flows are the water coming into the bathtub through the faucet and the water leaving the bathtub through the drain. Flows can happen between to stocks or a stock and a source that is not part of the model.

  • Connections between stocks and flows are drawn with double lines. The arrow points into the direction of the low (in or out). The node in the element of the flow line represents the amount of inflow or outflow. In some systems it also includes the convertor functionality.

Converter — takes input data and manipulates or convert that input into some output signal. In the bathtub example, if you were to turn the valve that controls the water flow in your bathtub, the converter would take as an input your action on the valve and convert that signal into an output reflecting the flow of water.

Connector — A connector is an arrow that allows information to pass between converters and converters, stocks and converters, stocks and flows, and converters and flows.

  • All the other connects are used to indicated mathematical dependencies. Connections of converters with converters, converters with flows or stocks, or stocks with flows are drawn with single lines. The arrow points to the elements that uses information (output) from the other.

In other systems, only flows can include computations, and instead of converters there are only constants.

Simple predation system[edit | edit source]

Below is a simple example model found in Wikipedia made with the STELLA software. It does not really represent a dynamic system, since there is only a simple inflow (birth of cats) and outflow (death of cats). It just shows the main elements.

A simple STELLA model of a cat population; stocks are represented as rectangles, flows as pipes to/from the stock, converters as the circles, and connectors as the curved red lines with arrows. (transcluded from Wikipedia)

The following picture shows the same model made with FreeStyler

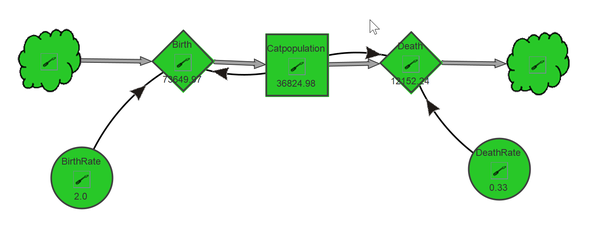
Simple cats model made with the Free Styler plugin. Graphics are a bit different, e.g. flows are made of one anonymous source, a rate and a stock with two flow connectors.

The most simple systems that are taught to understand system dynamics are simple predation systems. The following model[3] found as the NetLogo [4] library shows a Wolf Sheep predation systems using Lotka-Volterra equations [5].

See also more detailed examples:

Benefits in education[edit | edit source]

The main authors of the system dynamics approach put forward similar arguments as other approaches in (educational)computer simulation. Martin (1997) [2] observes that students are often unable to complete task because they have a mental model that does not fit reality. “A mental model is one’s mental perception or representation of system interactions and the behavior those interactions can produce. Due to an incomplete or incorrect mental model, a student cannot apply the principles taught in lectures to tasks in life.” Martin (1997:8).

According to this tutorial [2], “System dynamics offers a source of direct and immediate feedback for students to test assumptions about their mental models of reality through the use of computer simulation. Computer simulation is the imitation of system behavior through numerical calculations performed by a computer on a system dynamics model. A system dynamics model is the representation of the structure of a system. Once a system dynamics model is constructed and the initial conditions are specified, a computer can simulate the behavior of the different model variables over time.”

As with other approaches, the question is how to scaffold learner activities as discussed in the guided discovery learning learning model [6]. In their literature review, de Jong & Joolingen (1998) note: “The general conclusion that emerges from these studies is that there is no clearand univocal outcome in favor of simulations. An explanation why simulation based learning does not improve learning results can be found in the intrinsic problems that learners may have with discovery learning”. For example, students do not know what a hypothesis is, they can not state or adapt hypothesis on the basis of collected data, they are resistent to change and have confirmation biases and a fear of rejecting hypothesis. Furthermore, they tend not to using the whole range of experiments and have a tendency to play with may parameters at the same without really wanting to engage in systematic testing.

Successful learners “successful learners use systematic planning and monitoring, whereas unsuccessful learners work in an unsystematic way” (p.8) [6]. It therefore is important to provide students with instructional aids that helps them engaging them in mental activities that are beneficial for learning. de Jong & Joolingen (1998) mention direct access to domain knowledge, support for hypothesis generation, support for design of experiments, support for making predictions and finally support for (several) regulative learning processes. All as opposed to "playing" without much thinking)

In the same vein, students will learn better, if they build their own system.

Software[edit | edit source]

Free


Commercial:

  • STELLA, probably the most popular commercial system used in education. Several versions exist, including an extension to create "engaging" interfaces. A free very limited online version is available (2 stocks).
  • iThink. Probably similar to "Stella architect", i.e. a simulation engine with additional interface features.
  • Simile from Simulistics. A commercial software.
  • SystemDynamics libary (free) for commercial Wolfram System Modeler

Web development platforms

  • sd.js - System Dynamics for the web Quote: A modern, high performance, open source system dynamics engine for today's web and tomorrow's. sd.js runs in all major browsers (Edge, Chrome, Firefox, Safari), and on the server under node.js.

Standards'

  • XMILE, OASIS XML Interchange Language (XMILE) for System Dynamics TC

Links[edit | edit source]

MIT System dynamics tutorials[edit | edit source]

A number of open courseware materials can be found, e.g.

Example PDFs

Other[edit | edit source]


For folks with math skills[edit | edit source]

Bibliography[edit | edit source]

cited with footnotes[edit | edit source]

  1. ↑ Meadows, Donella H; Meadows, Dennis L; Randers, Jørgen; Behrens III, William W (1972). The Limits to Growth; A Report for the Club of Rome's Project on the Predicament of Mankind (PDF). New York: Universe Books. ISBN 0876631650. Retrieved 26 November 2017.
  2. ↑ 2.0 2.1 2.2 Martin, Leslie A. (1997). The First Step, prepared for the MIT System Dynamics in Education Project Under the Supervision ofDr. Jay W. Forrester, Retrieved, March 2019 from https://ocw.mit.edu/courses/sloan-school-of-management/15-988-system-dynamics-self-study-fall-1998-spring-1999/readings/step.pdf
  3. ↑ Wilensky, U. (2005). NetLogo Wolf Sheep Predation (System Dynamics) model. http://ccl.northwestern.edu/netlogo/models/WolfSheepPredation(SystemDynamics). Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.
  4. ↑ Wilensky, U. (1999). NetLogo. http://ccl.northwestern.edu/netlogo/. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.
  5. ↑ Lotka, A.J. (1956). Elements of Mathematical Biology. New York: Dover.
  6. ↑ 6.0 6.1 de Jong, T. & van Joolingen, W. (1998). Scientific discovery learning with computer simulations of conceptual domains. Review of Educational Research, 68(2):179-201, 1998. Abstract/PDF Preprint

Other[edit | edit source]

  • Wilkerson, M., & Fenwick, M. (2017). The practice of using mathematics and computational thinking (pp. 181–204) in Helping students make sense of the world using next generation science and engineering practices Chapter: Publisher: National Science Teachers AssociationEditors: Christina V. Schwarz, Cynthia Passmore, Brian J. Reiser, https://www.researchgate.net/publication/316158531_The_practice_of_using_mathematics_and_computational_thinking
  • Introduction to System Dynamics Modeling with Dynamo (1981), George P. Richardson; Alexander L. Pugh III, Pegasus Communications, ISBN 1-883823-43-9
  • Modeling the Environment: An Introduction To System Dynamics Modeling Of Environmental Systems (1999), Andrew Ford, Island Press, ISBN 1-55963-601-7
    • Appendix D: Dynamo
  • "The Prophet of Unintended Consequences", Lawrence M. Fisher, strategy+business #40 Autumn 2005 [1]
  • Corporate Planning and Policy Design: A System Dynamics Approach (1981), James M. Lyneis, (MIT Press/Wright-Allen Series in System Dynamics) ISBN 0-262-12083-6
  • Modeling for Learning Organizations (2000), John D.W. Morecroft, John D. Sterman; Productivity Press (System Dynamics Series) (Hardcover) ISBN 1-56327-250-4
  • Dynamics of growth in a finite world (1974), Dennis L. Meadows, Wright-Allen Press, ISBN 0-9600294-4-3
    • Appendix C: How to Read a DYNAMO Flow Diagram;
    • Appendix D: How to Read Dynamo Equations
    • Appendix E: How to Read a DYNAMO Graphical Output
  • Computer-Assisted Theory Building: Modeling Dynamic Social Systems (1988), Dr. Robert Hanneman, Sage Publications, Inc., 0803929617
  • Computer Simulation in Management Science (1998), Michael Pidd, Wiley, ISBN 0-471-97931-7
  • Simulation for the social scientist (2005), G. Nigel Gilbert, Klaus G. Troitzsch, Open University Press, ISBN 0-335-21600-5

Studies made with system dynamics[edit | edit source]

Meadows, Donella; Randers, Jørgen; Meadows, Dennis (2004). The limits to growth: the 30-year update. Chelsea Green Pub. p. 285. ISBN 1-931498-51-2.

Karayanakis, Nicholas Mark (24 June 1993). Computer-assisted simulation of dynamic systems with block diagram languages. CRC Press. ISBN 0-8493-8971-2.

Swanson, Carl V.; Raymond J., Waldmann (September 1970). "A Simulation Model Of Economic Growth Dynamics". Journal of the American Planning Association. Routledge: Taylor & Francis Group. 36 (5): 314–322. doi:10.1080/01944367008977327. Retrieved 2010-05-12.

Taylor, Peter J. (2005). Unruly complexity: ecology, interpretation, engagement. University Of Chicago Press. ISBN 0-226-79036-3.

Licensed under CC BY-SA 3.0 | Source: https://edutechwiki.unige.ch/en/System_dynamics
43 views |
↧ Download this article as ZWI file
Encyclosphere.org EncycloReader is supported by the EncyclosphereKSF