Conformal invariants
 From Encyclopedia of Mathematics - Reading time: 18 min
From Encyclopedia of Mathematics - Reading time: 18 min
Let $( M , g )$ be any Riemannian manifold, consisting of a smooth manifold $M$ and a non-degenerate symmetric form $g$ on the tangent bundle of $M$, not necessarily positive-definite. By definition, for any strictly positive smooth function $\lambda : M \rightarrow \mathbf{R} ^ { + }$ the Riemannian manifold $( M , \lambda g )$ is conformally equivalent to $( M , g )$ (cf. also Conformal mapping), and a tensor $T ( g )$ (cf. also Tensor analysis) constructed from $g$ and its covariant derivatives is a conformal invariant if and only if for some fixed weight $k$ the tensor $\lambda ^ { k } T ( \lambda g )$ is independent of $\lambda$. The tensor $g$ is itself a trivial conformal invariant of weight $k = - 1$, and the dimension of $M$ and signature of $g$ can be regarded as trivial conformal invariants, of weight $k = 0$. However, there are many non-trivial conformal invariants of Riemannian manifolds of dimension $n > 2$, and non-trivial scalar conformal invariants have been the subject of much recent work, sketched below. One can also extend the definition to include conformal invariants that are not tensors; these will not be considered below.
An $n$-dimensional Riemannian manifold $( M , g )$ is flat in a neighbourhood $N \subset M$ of a point $P \in M$ if there are coordinate functions $x ^ { 1 } , \ldots , x ^ { p }$, $y ^ { 1 } , \dots , y ^ { q }$ such that
\begin{equation*} g = \{ d x ^ { 1 } \bigotimes d x ^ { 1 } + \ldots + d x ^ { p } \bigotimes d x ^ { p } \} + \end{equation*}
\begin{equation*} - \{ d y ^ { 1 } \bigotimes d y ^ { 1 } + \ldots + d y ^ { q } \bigotimes d y ^ { q } \} \end{equation*}
on $N$, where $p + q = n$ and $p - q$ is the signature of $g$. A manifold is (locally) conformally flat if it is locally conformally equivalent to a flat manifold; the modifier "locally" is a tacit part of the definition, normally omitted. Clearly, conformally flat manifolds have no non-trivial conformal invariants.
For any smooth manifold $M$, let $C ^ { \infty } ( M )$ be the ring of smooth real-valued functions $M \rightarrow \mathbf{R}$ (regarded as an algebra over $\mathbf{R}$), let $\cal E$ be the usual $C ^ { \infty } ( M )$-module of $1$-forms over $M$, and for any $r \geq 0$, let $\otimes ^ { r } \mathcal{E}$ denote the $r$-fold tensor product $\cal E \otimes \ldots \otimes E$ over $C ^ { \infty } ( M )$. In particular, the non-degenerate symmetric form $g$ of a Riemannian manifold will be regarded as a symmetric element of $\otimes ^ { 2 } \mathcal{E}$, as above. The conformal invariance condition $\lambda ^ { k } T ( \lambda g ) = T ( g )$ is entirely local, so that one may as well assume that $M$ is itself an open set in ${\bf R} ^ { n }$. One finds that the signature is of little interest in the construction of conformal invariants, since strategically placed $\pm$ signs turn constructions for the strictly Riemannian case $( p , q ) = ( n , 0 )$ into corresponding constructions for the general case. Hence the existence of conformal invariants depends only on the dimension $n$.
In the next few paragraphs the discussion of conformal invariants is organized by dimension $n$; at the end the discussion centres exclusively on recent work concerning scalar conformal invariants for the cases $n \geq 4$.
Dimension one.[edit]
Any $1$-dimensional Riemannian manifold $( M , g )$ is trivially conformally flat, so that there are no non-trivial conformal invariants in dimension $n = 1$.
Dimension two.[edit]
If $( M , g )$ is a Riemannian manifold of dimension $n = 2$, let
\begin{equation*} g = E d x \bigotimes d x + \end{equation*}
\begin{equation*} + F ( d x \bigotimes d y + d y \bigotimes d x ) + G d y \bigotimes d y \end{equation*}
in some neighbourhood of any point $P \in M$. The question of conformal flatness of $( M , g )$ breaks into two cases, as follows.
i) If $E G - F ^ { 2 } < 0$ the usual method of factoring $E s ^ { 2 } + 2 F s t + G t ^ { 2 } \in C ^ { \infty } ( M ) [ s , t ]$ into a product of two linear homogeneous factors leads to a product $\theta \otimes \varphi \in \otimes ^ { 2 } \mathcal{E}$ of linearly independent $1$-forms, whose symmetric part is $g = ( \theta \otimes \varphi + \varphi \otimes \theta ) / 2$. Since $n = 2$, there are smooth functions $\lambda$, $\mu$, $\rho$, $\sigma$ in a neighbourhood of $P$ such that $\theta = \lambda d \rho$ and $\varphi = \mu d \sigma$, so that $g = \lambda \mu ( d \rho \otimes d \sigma + d \sigma \otimes d \rho ) / 2$. By setting $\rho = u + v$ and $\sigma = u - v$, one then has $g = \lambda \mu ( d u \otimes d u - d v \otimes d v )$ in a neighbourhood of $P$; hence $( M , g )$ is conformally flat.
ii) The case $E G - F ^ { 2 } > 0$ is the classical problem of finding isothermal coordinates for a Riemann surface, first solved by C.F. Gauss in a more restricted setting. More recent treatments of the same problem are given in [a9], [a10], [a4]; these results are easily adapted to the smooth case to show that any (smooth) Riemannian surface $( M , g )$ with a positive-definite (or negative-definite) metric $g$ is conformally flat. It follows from i) and ii) that there are no non-trivial conformal invariants in dimension $n = 2$.
Dimension at least three.[edit]
Some classical conformal invariants in dimensions $n \geq 3$ are as follows (their constructions will be sketched later):
In 1899, E. Cotton [a7] assigned a tensor $C ( g ) \in \otimes ^ { 3 } \mathcal{E}$ to any Riemannian manifold $( M , g )$ of any dimension $n \geq 3$; it is conformally invariant of weight $k = 0$ only in the special case $n = 3$, and J.A. Schouten [a12] showed that in this case $( M , g )$ is conformally flat if and only if $C ( g ) = 0$.
In 1918, H. Weyl [a14] constructed a tensor $W ( g ) \in \otimes ^ { 4 } \mathcal{E}$ for any Riemannian manifold $( M , g )$ of dimension $n \geq 3$, conformally invariant of weight $k = - 1$ for all dimensions $n \geq 3$ although it vanishes identically for $n = 3$. Schouten [a12] showed that a Riemannian manifold $( M , g )$ of dimension $n \geq 4$ is conformally flat if and only if $W ( g ) = 0$, and $W ( g )$ is now known as the Weyl curvature tensor (cf. also Weyl tensor).
The remaining classical tensor $B ( g ) \in \otimes ^ { 2 } \mathcal{E}$ was constructed by R. Bach [a1] in 1921; although $B ( g )$ exists in any dimension $n \geq 3$, it is conformally invariant, of weight $k = 1$, only for Riemannian manifolds $( M , g )$ of dimension $n = 4$, and in this dimension $B ( g ) = 0$ if and only if $( M , g )$ is conformally equivalent to an Einstein manifold (see below).
Algebraic background.[edit]
The primarily algebraic background needed to describe these three classical conformal invariants is also needed to sketch the more recent construction of the scalar conformal invariants, mentioned earlier. Let $\mathcal{R}$ be any commutative ring with unit that is also an algebra over the real numbers; the ring $\mathcal{R}$ will later be $C ^ { \infty } ( M )$ for a smooth manifold $M$. Let $\cal E$ be an $\mathcal{R}$-module, let $\cal E_{*} = \operatorname { Hom } _ { R } ( E , R )$, let $\mathcal{E}_{ * *} = \operatorname { Hom } _ { \mathcal{R} } ( \mathcal{E}_ * , \mathcal{R} )$, and assume that the natural homomorphism from $\cal E$ to its double dual $\mathcal{E}_{ * *}$ is an isomorphism ${\cal E} \overset{\approx}{\to} {\cal E} _ {* * }$; the $\mathcal{R}$-module $\cal E$ will later be the $C ^ { \infty } ( M )$-module of $1$-forms on $M$, and $\mathcal{E} _ { * }$ will be the $C ^ { \infty } ( M )$-module of smooth vector fields on $M$. As before, for any $r \geq 0$ let $\otimes ^ { r } \mathcal{E}$ denote the $r$-fold tensor product over $\mathcal{R}$, later the $C ^ { \infty } ( M )$-module of contravariant tensors of degree $r$ over $M$.
If $\tau _ { 2 } : \otimes ^ { 2 } \mathcal{E} \rightarrow \otimes ^ { 2 } \mathcal{E}$ is the $\mathcal{R}$-module isomorphism that interchanges the two factors $\cal E$, an element $g \in \otimes ^ { 2 } \mathcal{E}$ is symmetric if $\tau _ { 2 } g = g$. Let $\mathsf{S} ^ { 2 } \mathcal{E} \subset \otimes ^ { 2 } \mathcal{E}$ be the submodule of symmetric elements; it consists of $\mathcal{R}$-linear combinations of products of the form $\theta \otimes \theta \in \mathsf{S} ^ { 2 } \mathcal{E}$. One can regard any $g \in \mathsf{S} ^ { 2 } \cal E$ as a homomorphism $g : \otimes ^ { 2 } \cal E * \rightarrow R$, so that there is an induced homomorphism 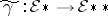 such that $\langle \tilde { \gamma } ( X ) , Y \rangle = g ( X \otimes Y ) \in \mathcal{R}$ for any $X \otimes Y \in \otimes ^ { 2 } \cal E_{*}$. The isomorphism ${\cal E} \overset{\approx}{\to} {\cal E} _ {* * }$ permits one to regard $\tilde{\gamma}$ as a homomorphism $\gamma : \mathcal{E}_{*} \rightarrow \mathcal{E}$, and $g$ is non-degenerate if $\gamma$ is an isomorphism. In this case the inverse $\gamma ^ { - 1 } : \cal E \rightarrow E *$ provides a unique element $g ^ { - 1 } \in \mathsf{S} ^ { 2 } \cal E _{*}$ that can be regarded as a homomorphism $g ^ { - 1 } : \otimes ^ { 2 } \mathcal{E} \rightarrow \mathcal{R}$ with values $g ^ { - 1 } ( \theta \otimes \varphi ) = \langle \theta , \gamma ^ { - 1 } ( \varphi ) \rangle \in \mathcal R $ for any $\theta \otimes \varphi \in \otimes ^ { 2 } \mathcal{E}$. One easily verifies that $g ^ { - 1 }$ is itself non-degenerate.
such that $\langle \tilde { \gamma } ( X ) , Y \rangle = g ( X \otimes Y ) \in \mathcal{R}$ for any $X \otimes Y \in \otimes ^ { 2 } \cal E_{*}$. The isomorphism ${\cal E} \overset{\approx}{\to} {\cal E} _ {* * }$ permits one to regard $\tilde{\gamma}$ as a homomorphism $\gamma : \mathcal{E}_{*} \rightarrow \mathcal{E}$, and $g$ is non-degenerate if $\gamma$ is an isomorphism. In this case the inverse $\gamma ^ { - 1 } : \cal E \rightarrow E *$ provides a unique element $g ^ { - 1 } \in \mathsf{S} ^ { 2 } \cal E _{*}$ that can be regarded as a homomorphism $g ^ { - 1 } : \otimes ^ { 2 } \mathcal{E} \rightarrow \mathcal{R}$ with values $g ^ { - 1 } ( \theta \otimes \varphi ) = \langle \theta , \gamma ^ { - 1 } ( \varphi ) \rangle \in \mathcal R $ for any $\theta \otimes \varphi \in \otimes ^ { 2 } \mathcal{E}$. One easily verifies that $g ^ { - 1 }$ is itself non-degenerate.
For any $r \geq 0$, let $\{ p , q \}$ be an unordered pair of distinct elements in $\{ 1 , \dots , r , r + 1 , r + 2 \}$ and let $g \in \mathsf{S} ^ { 2 } \cal E$ be non-degenerate. Then one can evaluate $g ^ { - 1 }$ on the tensor product $\mathcal{E} \otimes \mathcal{E}$ of the $p$th and $q$th factors of $\otimes ^ { r + 2 } \mathcal{E}$ to obtain a well-defined $\mathcal{R}$-linear contraction $g ^ { - 1 } \{ p , q \} : \otimes ^ { r + 2 } \mathcal{E} \rightarrow \otimes ^ { r } \mathcal{E}$. The symmetry of $g ^ { - 1 }$ guarantees that $g ^ { - 1 } \{ p , q \}$ does not require an ordering of $\{ p , q \}$. Similarly, if $\{ p , q , r , s \}$ is any unordered subset of $\{ 1 , \ldots , r , r + 1 , \ldots , r + 4 \}$, there is a well-defined $\mathcal{R}$-linear contraction $g ^ { - 1 } \{ p , q ; r , s \} : \otimes ^ { r + 4 } \mathcal{E} \rightarrow \otimes ^ { r } \mathcal{E}$, where $g ^ { - 1 } \{ p , q , r , s \} = g ^ { - 1 } \{ p , q \} g ^ { - 1 } \{ r , s \} = g ^ { - 1 } \{ r , s \} g ^ { - 1 } \{ p , q \}$.
An element $\Theta \in \otimes ^ { 2 } \mathcal{E}$ is alternating if $\tau _ { 2 } \Theta = - \Theta$, and there is a submodule $\mathsf{A} ^ { 2 } \mathcal{E} \subset \otimes ^ { 2 } \mathcal{E}$ that consists of all such alternating elements. If $\mathcal{R}$ is the ring $C ^ { \infty } ( M )$ for a Riemannian manifold $( M , g )$, and if $\cal E$ is the $\mathcal{R}$-module of $1$-forms on $M$, then the classical Riemannian curvature tensor of $( M , g )$ (cf. also Curvature tensor; Riemann tensor) is a symmetric element $R ( g ) \in \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E}$, for the submodule $\mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E} \subset \otimes ^ { 4 } \mathcal{E}$; a construction is sketched below. The corresponding Ricci curvature is the contraction $\operatorname { Ric } ( g ) = g ^ { - 1 } \{ 2,3 \} R ( g ) = g ^ { - 1 } \{ 1,4 \} R ( g ) \in \mathsf{S} ^ { 2 } \mathcal{E}$, and the corresponding scalar curvature is the contraction $S ( g ) = g ^ { - 1 } \{ 1,2 \} \operatorname { Ric } ( g ) = g ^ { - 1 } \{ 1,4 ; 2,3 \} R ( g ) \in C ^ { \infty } ( M )$. In case $M$ is of dimension $n \geq 3$, there is a nameless tensor
\begin{equation*} A ( g ) = \frac { 1 } { n - 2 } \left( \operatorname { Ric } ( g ) - \frac { 1 } { 2 } \frac { S ( g ) } { n - 1 } g \right) \in \mathsf{S} ^ { 2 } \cal E \end{equation*}
that is used to construct all three classical conformal invariants.
The construction of the Weyl curvature tensor $W ( g ) \in \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E}$ uses a $C ^ { \infty } ( M )$-module homomorphism from the submodule $\mathsf{S} ^ { 2 } \mathcal{E} \otimes \mathsf{S} ^ { 2 } \mathcal{E} \subset \bigotimes ^ { 4 } \mathcal{E}$ to the submodule of symmetric elements in $\mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E} \subset \otimes ^ { 4 } \mathcal{E}$. If $0 < p \leq 4$, let $\tau _ { p } : \otimes ^ { 4 } \mathcal{E} \rightarrow \otimes ^ { 4 } \mathcal{E}$ be the isomorphism that permutes the $p$th factor $\cal E$ in $\otimes ^ { 4 } \mathcal{E}$ to the left of the first $p - 1$ factors $\cal E$ in $\otimes ^ { 4 } \mathcal{E}$, so that $\tau _ { p }$ is cyclic in the usual sense that $\tau ^ { p_p } = 1$, and $\tau ^ { - 1 } p$ simply places the first factor into the $p$th slot; in particular, $\tau_1$ is the identity, and $\tau_2$ interchanges the first two factors as before. For any $h \otimes k \in \mathsf{S} ^ { 2 } \mathcal{E} \otimes \mathsf{S} ^ { 2 } \mathcal{E}$, set
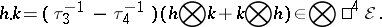 |
By looking at the special cases $h \otimes k = ( \theta \otimes \theta ) \otimes ( \varphi \otimes \varphi ) \in \mathsf{S} ^ { 2 } \mathcal{E} \otimes \mathsf{S} ^ { 2 } \mathcal{E}$, for any $\theta \in \mathcal{E}$ and $\varphi \in \mathcal{E}$, one obtains
\begin{equation*} h . k = ( \theta \bigotimes \varphi - \varphi \bigotimes \theta ) \bigotimes ( \theta \bigotimes \varphi - \varphi \bigotimes \theta ) \in \end{equation*}
\begin{equation*} \in \mathsf{A} ^ { 2 } {\cal E} \bigotimes \mathsf{A} ^ { 2 } {\cal E}; \end{equation*}
these cases induce the announced homomorphism $\mathsf{S} ^ { 2 } \mathcal{E} \otimes \mathsf{S} ^ { 2 } \mathcal{E} \rightarrow \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E}$.
For any Riemannian manifold $( M , g )$ of dimension $n \geq 3$, the Weyl curvature tensor is the difference $W ( g ) = R ( g ) - g \cdot A ( g ) \in \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E} $, which is a non-trivial conformal invariant of weight $k = - 1$ whenever $n \geq 4$. Although the principal feature of $W ( g )$ is that $W ( g ) = 0$ if and only if the Riemannian manifold $( M , g )$ of dimension $n \geq 4$ is conformally flat, it also provides a basic tool for constructing other conformal invariants for manifolds of dimensions $n \geq 4$. For example, for any $m > 0$, let $W ( g ) \otimes \ldots \otimes W ( g ) \in \otimes ^ { 4 m } \mathcal{E}$ be the tensor product of $m$ copies of $W ( g )$, and let $\{ p _ { 1 } , \dots , p _ { 4 m } \} = \{ 1 , \dots , 4 m \}$ as unordered sets. Then the contraction
\begin{equation*} g ^ { - 1 } \{ p _ { 1 } , p _ { 2 } ; \ldots ; p _ { 4 m - 1 } , p _ { 4 m } \} ( W ( g ) \bigotimes \ldots \bigotimes W ( g ) ) \end{equation*}
is a non-trivial scalar conformal invariant $\operatorname{contr}( W ( g ) \otimes \ldots \otimes W ( g ) ) \in C ^ { \infty } ( M )$ of weight $ k = + m$ for any Riemannian manifold $( M , g )$ of dimension $n \geq 4$.
The curvatures $R ( g )$, $\operatorname { Ric } ( g )$, $S ( g )$, and the tensor $A ( g )$ assigned to any Riemannian manifold $( M , g )$ are all constructed via the Levi-Civita connection associated to $g$, defined below, so that $W ( g ) \in \otimes ^ { 4 } \mathcal{E}$ depends implicitly upon the Levi-Civita connection. The remaining classical conformal invariants $C ( g ) \in \otimes ^ { 3 } \mathcal{E}$ and $B ( g ) \in \otimes ^ { 2 } \mathcal{E}$, for Riemannian manifolds of dimensions $n = 3$ and $n = 4$, respectively, as well as most of the scalar conformal invariants that will be introduced below, will be constructed explicitly via a version of the Levi-Civita connection that is sketched in the next two paragraphs; more details of this version appear in [a11].
Levi-Civita connection.[edit]
For any smooth manifold $M$ with $C ^ { \infty } ( M )$-module $\cal E$ of $1$-forms as before, a connection (cf. also Connections on a manifold) is a sequence of real linear homomorphisms $\nabla : \otimes ^ { r } \mathcal{E} \rightarrow \otimes ^ { r+ 1 } \mathcal{E}$ such that the complex $\{ \otimes ^ { * } {\cal E} , \nabla \}$ covers the classical de Rham complex $\{ \wedge ^ { * } \mathcal{E} , d \}$ (cf. also Differential form); that is, the diagram
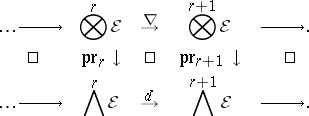 |
commutes for the usual projections 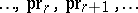 from tensor products to exterior products over $C ^ { \infty } ( M )$, where $\wedge ^ { * } \mathcal{E}$ is the quotient of $\otimes ^ { * } \mathcal E$ by the two-sided ideal generated by $\mathsf{S} ^ { 2 } \cal E \subset \otimes ^ { * } E$. Furthermore, if $0 \leq p \leq r$ and if $\tau _ { p + 1 } : \otimes ^ { p + q + 1 } \mathcal{E} \rightarrow \otimes ^ { p + q + 1 } \mathcal{E}$ is the permutation with parity $( - 1 ) ^ { p } \in \{ - 1 , + 1 \}$ that moves the $( p + 1 )$st factor $\cal E$ to the left of the first $p$ factors $\cal E$, then
from tensor products to exterior products over $C ^ { \infty } ( M )$, where $\wedge ^ { * } \mathcal{E}$ is the quotient of $\otimes ^ { * } \mathcal E$ by the two-sided ideal generated by $\mathsf{S} ^ { 2 } \cal E \subset \otimes ^ { * } E$. Furthermore, if $0 \leq p \leq r$ and if $\tau _ { p + 1 } : \otimes ^ { p + q + 1 } \mathcal{E} \rightarrow \otimes ^ { p + q + 1 } \mathcal{E}$ is the permutation with parity $( - 1 ) ^ { p } \in \{ - 1 , + 1 \}$ that moves the $( p + 1 )$st factor $\cal E$ to the left of the first $p$ factors $\cal E$, then
\begin{equation*} \nabla ( \Theta \bigotimes \Phi ) = \nabla \Theta \bigotimes \Phi + \tau _ { p + 1 } ( \Theta \bigotimes \nabla \Phi ) \in \end{equation*}
\begin{equation*} \in \bigotimes \square ^ { p + q + 1 } \mathcal{E} \end{equation*}
for any $\in \otimes ^ { p } \mathcal{E}$ and $\Phi \in \otimes ^ { q} \mathcal{E}$; the product rule is
\begin{equation*} \nabla ( a \Phi ) = d a \bigotimes \Phi + a \nabla \Phi \in \bigotimes \square ^ { q + 1 } \mathcal{E} \end{equation*}
for $a \in C ^ { \infty } ( M )$. It follows that the covering $\{ \otimes ^ { * } {\cal E} , \nabla \}$ of $\{ \wedge ^ { * } \mathcal{E} , d \}$ also preserves products. If $( M , g )$ is a Riemannian manifold, with metric $g \in \mathsf{S} ^ { 2 } \cal E$ as usual, there is a unique connection $\{ \otimes ^ { * } {\cal E} , \nabla \}$ such that $\nabla g = 0 \in \otimes ^ { 3 } \mathcal{E}$; this is the Levi-Civita connection associated to $( M , g )$ (cf. also Levi-Civita connection).
One useful property of any connection $\{ \otimes ^ { * } {\cal E} , \nabla \}$ for any smooth manifold $M$ is that for any $r \geq 0$ the composition
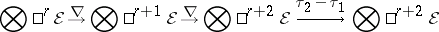 |
is $C ^ { \infty } ( M )$-linear, where $\tau_2$ interchanges the first two factors $\cal E$ of $\otimes ^ { r + 2 } \mathcal{E}$ and $\tau_1$ is the identity isomorphism; for any $r \geq 0$ the homomorphism $( \tau _ { 2 } - \tau _ { 1 } ) \circ \nabla \circ \nabla$ is the curvature operator $R ( \nabla ) : \otimes ^ { r } {\cal E} \rightarrow \otimes ^ {r + 2 } {\cal E}, $. In particular, for any Riemannian manifold $( M , g )$ and corresponding Levi-Civita connection, the tensor product of $R ( \nabla ) : \mathcal{E} \rightarrow \otimes ^ { 3 } \mathcal{E}$ and the identity isomorphism $1 : \mathcal{E} \rightarrow \mathcal{E}$ restricts to a $C ^ { \infty } ( M )$-linear mapping $R ( \nabla ) \otimes {\bf 1} : \mathsf{S} ^ { 2 } {\cal E} \rightarrow \otimes ^ { 4 } {\cal E}$, and the image $( R ( \nabla ) \otimes 1 ) g \in \otimes ^ { 4 } \mathcal{E}$ of the metric $g \in \mathsf{S} ^ { 2 } \cal E$ itself is the Riemannian curvature tensor $R ( g )$, lying in the submodule $\mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E} \subset \otimes ^ { 4 } \mathcal{E}$.
Even though the Levi-Civita connection $\{ \otimes ^ { * } {\cal E} , \nabla \}$ of a Riemannian manifold $( M , g )$ is defined in part by the requirement that $\nabla g = 0 \in \otimes ^ { 3 } \mathcal{E}$ for the Riemannian metric $g \in \mathsf{S} ^ { 2 } \cal E$, observe that the definition $R ( g ) = ( R ( \nabla ) \otimes 1 ) g$ of the Riemannian curvature is obtained by applying the curvature operator $( \tau _ { 2 } - \tau _ { 1 } ) \circ \nabla \circ \nabla$ only to the first factor of $g$. Consequently, $R ( g )$, $\operatorname { Ric } ( g )$, $S ( g )$, and $A ( g )$ all require the first two derivatives of $g$, in the obvious sense. The same remark applies to the Weyl curvature tensor $W ( g ) = R ( g ) - g \cdot A ( g ) \in \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E} $.
Cotton tensor.[edit]
Let $( M , g )$ be any Riemannian manifold of dimension $n \geq 3$, with $A ( g ) \in \mathsf{S} ^ { 2 } \mathcal{E}$ as before, let
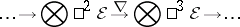 |
be the Levi-Civita connection, which restricts to $\mathsf{S} ^ { 2 } \mathcal{E} \subset \otimes ^ { 2 } \mathcal{E}$, and let $\tau _ { 3 } : \otimes ^ { 3 } {\cal E} \rightarrow \otimes ^ { 3 } {\cal E}$ be the cyclic permutation of the factors $\cal E$ that moves the third factor $\cal E$ to the left of the first two factors $\cal E$. The Cotton tensor is
\begin{equation*} C ( g ) = \nabla A ( g ) - \tau ^ { - 1_3 } \nabla A ( g ) \in \bigotimes \square ^ { 3 } \mathcal{E}, \end{equation*}
which visibly depends on third derivatives of $g$; this is equivalent to the original definition of E. Cotton [a7], and it has the evident cyclic symmetry $C ( g ) + \tau _ { 3 } C ( g ) + \tau ^ { 2_3} C ( g ) = 0$. Furthermore, $C ( g )$ is a conformal invariant if $M$ is of dimension $n = 3$, and Schouten [a12] showed in this case that $C ( g ) = 0 \in \otimes ^ { 3 } \mathcal{E}$ if and only if $( M , g )$ is conformally flat, as noted earlier.
Closed oriented $3$-dimensional Riemannian manifolds.[edit]
If one considers closed oriented $3$-dimensional Riemannian manifolds $( M , g )$, the Chern–Simons invariant $\Phi \{ M , g \} \in S ^ { 1 } ( = \mathbf{R} / \mathbf{Z} )$ is shown in [a6] to depend only on the conformal equivalence class $\{ M , g \}$ of $( M , g )$, and $\Phi \{ M , g \} \in S ^ { 1 }$ is a critical value if and only if $\{ M , g \}$ is conformally flat. S.S. Chern [a5] gave a simplified proof of this result by using the criterion $C ( g ) = 0$ of the preceding paragraph.
Bach tensor.[edit]
For any Riemannian manifold $( M , g )$ of dimension $n \geq 3$, the Bach tensor is
\begin{equation*} B ( g ) = \end{equation*}
\begin{equation*} = g ^ { - 1 } \{ 1,4 \} \nabla C ( g ) - g ^ { - 1 } \{ 1,3 ; 2,5 \} ( A ( g ) \bigotimes W ( g ) ) \subset \subset \bigotimes \square ^ { 2 } \mathcal{E}, \end{equation*}
for the Levi-Civita connection
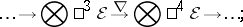 |
one easily verifies that the Bach tensor is an element of $\mathsf{S} ^ { 2 } \mathcal{E} \subset \otimes ^ { 2 } \mathcal{E}$. It is conformally invariant only in the special case $n = 4$, and in that case one has $B ( g ) = 0$ if and only if $( M , g )$ is conformally equivalent to a Riemannian manifold $( \widetilde { M } , \widetilde{g} )$ such that the Ricci curvature $\operatorname{Ric}( \tilde{g} ) \in \mathsf{S} ^ { 2 } \tilde {\cal E }$ is a constant multiple of the metric $\tilde{g} \in \mathsf{S} ^ { 2 } \mathcal{E}$ itself. Riemannian manifolds with the latter property are known as Einstein manifolds.
Recall that for any $m > 0$ the contractions
\begin{equation*} \text{ contr } ( W ( g ) \bigotimes \ldots \bigotimes W ( g ) ) = \end{equation*}
\begin{equation*} = g ^ { - 1 } \{ p _ { 1 } , p _ { 2 } ; \ldots ; p _ { 4 m - 1 } , p _ { 4 m } \} ( W ( g ) \bigotimes \ldots \bigotimes W ( g ) ) \in \in C ^ { \infty } ( M ) \end{equation*}
of the $m$-fold tensor product of the Weyl curvature tensor $W ( g ) \in \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E}$ are scalar conformal invariants of weight $k = m$, and observe that any $C ^ { \infty } ( M )$-linear combination of such contractions is also a scalar conformal invariant of weight $k = m$. Such scalar conformal invariants involve the Riemannian metric $g$ and its first and second order derivatives. However, the derivative 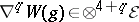 is not itself conformally invariant if $q > 0$, so that in general one cannot expect contractions of products
is not itself conformally invariant if $q > 0$, so that in general one cannot expect contractions of products 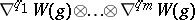 to produce conformal invariants if $q_ 1 + \ldots + q_ m > 0$. The following observations suggest a reasonable modification of the construction.
to produce conformal invariants if $q_ 1 + \ldots + q_ m > 0$. The following observations suggest a reasonable modification of the construction.
First, observe that if $( M , g )$ and $( \widetilde { M } , \widetilde{g} )$ are Riemannian manifolds for which there is an embedding $M \subset \tilde { M }$ with $\tilde { g } | _ { M } = g$, then any scalar conformal invariant of $( \widetilde { M } , \widetilde{g} )$ restricts to the corresponding scalar conformal invariant of $( M , g )$. Since the construction of conformal invariants is an entirely local question, it suffices to consider embeddings of open sets $M \subset {\bf R} ^ { n }$ into open sets $\tilde { M } \subset \mathbf{R} ^ { n } \times ( 0 , \infty ) \times ( - 1 , + 1 )$, for example. The hypotheses can be weakened if the conformal equivalence class of $( M , g )$ has a real-analytic representative with coordinates $x = ( x _ { 1 } , \ldots , x _ { n } )$. One can then assign a coordinate $t \in ( 0 , \infty )$ and use power series about $r = 0 \in ( - 1 , + 1 )$ to describe the Riemannian metric $\tilde { g }$ of an embedding, knowing that only the restrictions of the derivatives 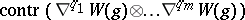 to the submanifold $M \subset \tilde { M }$ are of any interest, the inclusion being
to the submanifold $M \subset \tilde { M }$ are of any interest, the inclusion being
\begin{equation*} M \times \{ 1 \} \times \{ 0 \} \subset M \times ( 0 , \infty ) \times ( - 1 + 1 ). \end{equation*}
The second observation is a classical result, not directly related to conformal invariants. Given any Riemannian manifold $( \widetilde { M } , \widetilde{g} )$, with Levi-Civita connection $\{ \otimes ^ { * } \tilde { \mathcal{E} } , \tilde { \nabla } \}$ and Riemannian curvature $R (\tilde{ g} )$, if $q _ { 1 } + \ldots + q _ { m }$ is an even number, then the contractions $\operatorname {contr} ( \tilde { \nabla } ^ { q _ { 1 } } R ( \tilde{g} ) \otimes \ldots \otimes \tilde { \nabla } ^ { q _ { m } } R ( \tilde{g} ) )$ involve derivatives of $\tilde { g }$ of order up to $\operatorname { max } \{ q _ { 1 } + 2 , \ldots , q _ { m } + 2 \}$; furthermore, such contractions are visibly coordinate-free. Results in [a15] imply that if $( M , g )$ is locally real-analytic, then any coordinate-free polynomial combination of $\operatorname { det } \tilde{g} ^ { - 1 }$ and the components of the derivatives $\tilde { \nabla } ^ { q } R ( \tilde { g } )$ is a $C ^ { \infty } ( \widetilde { M } )$-linear combination of such contractions, which are known as Weyl invariants.
The third observation is that if $( \widetilde { M } , \widetilde{g} )$ is a Ricci-flat Riemannian manifold, in the sense that $\operatorname { Ric } ( \tilde{g} ) = 0 \in \mathsf{S} ^ { 2 } \tilde{\mathcal{E}}$, then $S ( \widetilde{g} ) = 0 \in C ^ { \infty } ( \widetilde { M } )$ so that $A ( \tilde{g} ) = 0 \in \mathsf{S} ^ { 2 } \tilde{\mathcal{E}}$; in this case the Riemannian curvature tensor itself is a classical conformal invariant: $R ( \tilde{ g } ) = W ( \tilde { g } ) \in \mathsf{A} ^ { 2 } \mathcal{E} \otimes \mathsf{A} ^ { 2 } \mathcal{E}$. Even though one cannot expect the derivatives $\tilde { \nabla } ^ { q } W ( \tilde { g } )$ nor contractions of products of such derivatives to be conformal invariants, the identifications 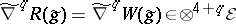 suggest that the contractions
suggest that the contractions 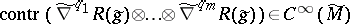 may be of value in the Ricci-flat case, whenever $q _ { 1 } + \ldots + q _ { m }$ is an even number.
may be of value in the Ricci-flat case, whenever $q _ { 1 } + \ldots + q _ { m }$ is an even number.
General construction of scalar conformal invariants.[edit]
The preceding observations lead to a general construction of scalar conformal invariants of $( M , g )$, with a dimensional restriction that will be specified later. One first covers $M$ by sufficiently small coordinate neighbourhoods $N$ and writes $( N , g )$ for each resulting Riemannian manifold $( N , g | _ { N } )$. For each $( N , g )$ C. Fefferman and C.R. Graham [a8] use a technique that appeared independently in [a13] to introduce a codimension-$2$ embedding $N \subset \tilde { N }$, described later, and to devise a Cauchy problem whose solution provides a Ricci-flat manifold $( \widetilde { N } , \widetilde{g} )$ with $\tilde { g } | _ { N } = g$. A further feature of the construction guarantees that any Weyl invariant in $C ^ { \infty } ( \tilde { N } )$ restricts to a conformal invariant of $( N , g )$, of weight $k = m + ( q _ { 1 } + \ldots + q _ { m } ) / 2$. Since $C ^ { \infty } ( N )$-linear combinations of scalar conformal invariants of weight $k$ are also scalar conformal invariants of weight $k$, for any fixed $m$-tuple $( q _ { 1 } , \dots , q _ { m } )$ of non-negative integers with an even sum one can use a smooth partition of unity subordinate to the covering of $M$ by the coordinate neighbourhoods $N$ to obtain a scalar conformal invariant of $( M , g )$ itself, known as a Weyl conformal invariant.
T.N. Bailey, M.G. Eastwood and Graham [a2] completed the proof of the following Fefferman–Graham conjecture [a8], which depends upon the parity of $n = \operatorname { dim } M$: If $( M , g )$ is a Riemannian manifold of odd dimension $n$, then every scalar conformal invariant of $( M , g )$ is a Weyl conformal invariant. If $( M , g )$ is a Riemannian manifold of even dimension $n$, then the preceding statement is true only for scalar conformal invariants of weight $k < n / 2$, and there is a conformally invariant element in $\mathsf{S} ^ { 2 } \mathcal{E}$ of weight $k = - 1 + n / 2$ that serves as an obstruction to finding a formal power series solution of the Cauchy problems used to construct the ambient manifolds $( \widetilde { N } , \widetilde{g} )$; the obstruction vanishes if $( M , g )$ is conformally equivalent to an Einstein manifold; if $n = 4$ the obstruction is the Bach conformal invariant $B ( g )$.
There are some exceptional scalar conformal invariants for even dimensions $n$ and weight $k \geq n / 2$, first observed in [a2]; the catalogue of all such exceptional invariants was completed in [a3].
Fefferman–Graham method.[edit]
This method, introduced in [a8], allows one to construct the codimension-$2$ embeddings $N \subset \tilde { N }$ of the Riemannian manifolds $( N , g )$, and to formulate the Cauchy problems whose solutions turn each ambient space $\widetilde { N } = N \times ( 0 , \infty ) \times ( - 1 , + 1 )$ into a Ricci-flat manifold $( \widetilde { N } , \widetilde{g} )$ with the desired properties.
One starts with the fibration over $N$ in which the fibre over each $P \in N$ consists of positive multiples $t^{2} g (P)$ of the metric $g ( P )$ at $P$; one may as well suppose that $t > 0$. The multiplicative group $\mathbf{R} ^ { + } = ( 0 , \infty )$ of real numbers $s > 0$ acts on the fibres by mapping $t ^ { 2 } g ( P )$ into $s ^ { 2 } t ^ { 2 } g ( P )$, and this permits one to regard the fibration as a fibre bundle with structure group $\mathbf{R} ^ { + }$ (cf. also Principal fibre bundle). Clearly, any section of the fibre bundle can be regarded as a Riemannian manifold that is conformally equivalent to $( N , g )$.
Let $\pi _ { 0 } : N _ { 0 } \rightarrow N$ be the corresponding principal fibre bundle, and observe that since $\operatorname { dim } N _ { 0 } = \operatorname { dim } N + 1$, the pullback $\pi ^ { * _ { 0 }} g \in \mathsf{S} ^ { 2 } {\cal E} _ { 0 }$ of the metric $g \in \mathsf{S} ^ { 2 } \cal E$ over $N$ needs at least one additional term to serve as a Riemannian metric over $N_ 0 $. It is useful to replace $\pi _ { 0 } : N _ { 0 } \rightarrow N$ by another $\mathbf{R} ^ { + }$-bundle $\widetilde{\pi} : \widetilde{N} \rightarrow N$ with $\widetilde { N } = N _ { 0 } \times ( - 1 , + 1 )$, and to try to construct a (non-degenerate) metric $\tilde{g} \in \mathsf{S} ^ { 2 } \tilde{\cal E}$ on $\tilde { N }$ such that
1) the restriction $\tilde{g} | _ { N _ { 0 } \times \{ 0 \}}$ is $\pi _ { 0 } ^ { * } \tilde{g}$;
2) the group elements $s \in \mathbf{R} ^ { + }$ map $\tilde{g} \in \mathsf{S} ^ { 2 } \tilde{\cal E}$ into $s ^ { 2 } \tilde { g } \in \mathsf{S} ^ { 2 } \tilde{\mathcal{E}}$ over all of $\tilde { N }$;
3) $( \widetilde { N } , \widetilde{g} )$ is Ricci-flat, with the consequence $W ( \tilde { g } ) = R ( \tilde { g } ) \in \mathsf{A} ^ { 2 } \tilde{\mathcal{E}} \otimes \mathsf{A} ^ { 2 } \tilde{\mathcal{E}}$ noted earlier. There is an implicit additional assumption, that the conformal equivalence class containing $( N , g )$ is real-analytic in the sense that there is a representative $( N , \lambda g )$ of the conformal class of $( N , g )$ for which one can choose coordinates $x = ( x ^ { 1 } , \dots , x ^ { n } )$ in $C ^ { \infty } ( N )$ such that $\lambda g = \sum _ { i ,\, j } \lambda g_ { i j } d x ^ { i } \otimes d x ^ { j } \in \mathsf{S} ^ { 2 } \mathcal{E}$, for coefficients $\lambda g_{ij} \in C ^ { \infty } ( N )$ that are real-analytic functions of $x$; one may as well assume that $( N , g )$ itself has this property.
The Fefferman–Graham method [a8] leads to a metric of the form
\begin{equation*} \tilde { g } = t ^ { 2 } \sum _ { i ,\, j } \tilde { g } _ { i j } ( x , t ) d x ^ { i } \bigotimes d x ^ { j } + \end{equation*}
\begin{equation*} + 2 r d t \bigotimes d t + t d t \bigotimes d r + t d r \bigotimes d t \end{equation*}
that satisfies 1)–3) for all $( x , t , r ) \in N \times ( 0 , \infty ) \times ( - 1 , + 1 )$ ($= \widetilde { N }$), for real-analytic functions $\tilde{g} _ { i j }$ of $( x , r )$ that satisfy the initial condition 1), $\tilde{g} _ { i j } ( x , 0 ) = g _ { i j } ( x )$ as formal power series about $r = 0 \in ( - 1 , + 1 )$; convergence is obtained in some neighbourhood of $r = 0$. Observe that the metric $\tilde{g} \in \mathsf{S} ^ { 2 } \mathcal{E}$ trivially satisfies the homogeneity condition 2) over all of $\tilde { N }$. The Riemannian curvature $R (\tilde{ g} )$ is itself conformally invariant by the consequence $R ( \tilde{ g } ) = W ( \tilde { g } ) \in \mathsf{A} ^ { 2 } \tilde{ \mathcal{E} } \otimes \mathsf{A} ^ { 2 } \tilde{ \mathcal{E} }$ of condition 3), and the homogeneity condition implies that any Weyl invariant 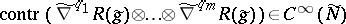 restricts over the section $N = N \times \{ 1 \} \times \{ 0 \}$ of $\widetilde { N } = N \times ( 0 , \infty ) \times ( - 1 , + 1 )$ to a Weyl conformal invariant in $C ^ { \infty } ( N )$, as required.
restricts over the section $N = N \times \{ 1 \} \times \{ 0 \}$ of $\widetilde { N } = N \times ( 0 , \infty ) \times ( - 1 , + 1 )$ to a Weyl conformal invariant in $C ^ { \infty } ( N )$, as required.
References[edit]
| [a1] | R. Bach, "Zur Weylschen Relativitätstheorie und der Weylschen Erweiterung des Krümmungstensorbegriffs" Math. Z. , 9 (1921) pp. 110–135 (Also: Jahrbuch 48, 1035) MR1544454 Zbl 48.1035.01 |
| [a2] | T.N. Bailey, M.G. Eastwood, C.R. Graham, "Invariant theory for conformal and CR geometry" Ann. of Math. , 139 : 2 (1994) pp. 491–552 MR1283869 Zbl 0814.53017 |
| [a3] | T.N. Bailey, A.R. Gover, "Exceptional invariants in the parabolic invariant theory of conformal geometry" Proc. Amer. Math. Soc. , 123 (1995) pp. 2535–2543 MR1243161 Zbl 0844.53008 |
| [a4] | S.S. Chern, "An elementary proof of the existence of isothermal parameters on a surface" Proc. Amer. Math. Soc. , 6 (1955) pp. 771–782 MR0074856 Zbl 0066.15402 |
| [a5] | S.S. Chern, "On a conformal invariant of three-dimensional manifolds" , Aspects of Math. and its Appl. , North-Holland (1986) pp. 245–252 MR0849555 Zbl 0589.53011 |
| [a6] | S.S. Chern, J. Simons, "Characteristic forms and geometric invariants" Ann. of Math. , 99 (1974) pp. 48–69 MR0353327 Zbl 0283.53036 Zbl 0591.53050 |
| [a7] | E. Cotton, "Sur les variétes à trois dimensions" Ann. Fac. Sci. Toulouse , 1 (1899) pp. 385–438 (Also: Jahrbuch 30, 538-539) MR1508211 Zbl 30.0538.01 |
| [a8] | C. Fefferman, C.R. Graham, "Conformal invariants" , The Mathematical Heritage of Élie Cartan (Lyon, 1984) , Astérisque (1985) pp. 95–116 MR0837196 Zbl 0602.53007 |
| [a9] | A. Korn, "Zwei Anwendungen der Methode der sukzessiven Anwendungen" Schwarz Festschrift (1914) pp. 215–229 (Also: Jahrbuch 45, 568) Zbl 45.0568.01 |
| [a10] | L. Lichtenstein, "Zur Theorie der konformen Abbildungen nichtanalytischer, singularitätenfreier Flächenstücke auf ebene Gebiete" Bull. Internat. Acad. Sci. Gracovie, Cl. Sci. Math. Nat. Ser. A. (1916) pp. 192–217 (Also: Jahrbuch 46, 547) |
| [a11] | H. Osborn, "Affine connection complexes" Acta Applic. Math. (to appear) MR1741659 Zbl 0956.53014 |
| [a12] | J.A. Schouten, "Über die konforme Abbildung $n$-dimensionaler Mannigfaltigkeiten mit quadratischer Maß bestimmung auf eine Mannigfaltigkeit mit euklidischer Maß bestimmung" Math. Z. , 11 (1921) pp. 58–88 (Also: Jahrbuch 48, 857-858) |
| [a13] | J.A. Schouten, J. Haantjes, "Beitgräge zur allgemeinen (gekrümmten) konformen Differentialgeometrie I–II" Math. Ann. , 112/113 (1936) pp. 594–629; 568–583 |
| [a14] | H. Weyl, "Reine Infinitesimalgeometrie" Math. Z. , 2 (1918) pp. 384–411 (Also: Jahrbuch 46, 1301) MR1544327 Zbl 46.1301.01 |
| [a15] | H. Weyl, "The classical groups" , Princeton Univ. Press (1939) (Reprint: 1946) MR0000255 Zbl 0020.20601 Zbl 65.0058.02 |
 KSF
KSF