Convex metric

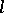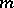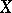An internal metric on a two-dimensional manifold which meets some convexity condition. More exactly, let and be two shortest lines issuing from some point ; let and 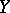be points on these lines; let be the distances from 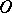to and 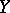, respectively; let be the distance between 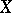and 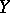; and let 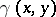be the angle opposite to the side in the plane triangle with sides 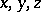. The convexity condition of the metric (at the point 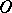) is that 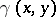is a non-increasing function (i.e. 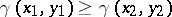if 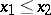, ) on any pair of intervals 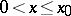, 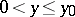such that the points 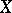and 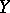, which correspond to two arbitrary values in these intervals, can be connected by a shortest line. An internal metric is a convex metric if and only if it is a metric of non-negative curvature. The metric of a convex surface is a convex metric. Conversely, any two-dimensional manifold with a convex metric can be realized as a convex surface (Aleksandrov's theorem).

References[edit]