Convexity radius
From Encyclopedia of Mathematics - Reading time: 1 min
convexity limit, 
, of a function 
The least upper bound of the radii 
of the spheres 
, each one of which is mapped into a convex domain; here, the function 
is defined on a domain 
of a metric space with metric 
and assumes values in a linear space. The convexity radius 
at a point 
with respect to some class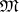 
of mappings 
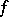of the domain 
is, by definition, the number
 |
If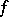 
is an affine mapping of a Euclidean space 
, 
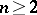, then 
. With respect to the class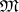 
of all normalized univalent conformal mappings 
, 
, 
, of the unit disc 
of the complex plane, the convexity radius equals 
; if one imposes the additional condition of convexity of the domains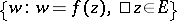 
, i.e. for convex functions (cf. Convex function (of a complex variable)), 
. See also Univalent function.
References[edit]
| [1] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [2] | I.A. Aleksandrov, "On bounds for convexity and starlikeness of functions univalent and regular in a disc" Dokl. Akad. Nauk SSSR , 116 : 6 (1957) pp. 903–905 (In Russian) |
| [3] | A. Marx, "Untersuchungen über schlichte Abbildungen" Math. Ann. , 107 (1932) pp. 40–67 |
EncycloReader
is supported by the 
KSF