Edgeworth series

2020 Mathematics Subject Classification: Primary: 60F05 [MSN][ZBL]

The series defined by

(*)

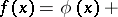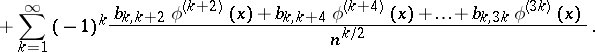Here is the distribution density of the random variable

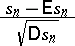(, where are independent and identically distributed),

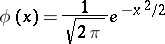is the density of the standard normal distribution, and

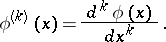The coefficients , , 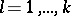do not depend on and are polynomials with respect to 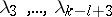, where , 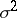is the variance, and 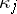is the semi-invariant of order 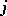of 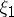. In particular, the first terms of the expansion have the form

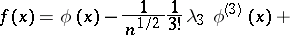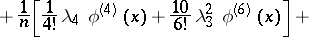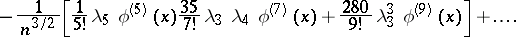The coefficients 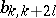can also be expressed in terms of the central moments.

The series (*) were introduced by F.Y. Edgeworth [E]. Their asymptotic properties have been studied by H. Cramér, who has shown that under fairly general conditions the series (*) is the asymptotic expansion of 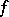in which the remainder has the order of the first discarded term.

References[edit]

Comments[edit]

The above discussion omits many technical details as well as modern developments.

An excellent account of the theory of Edgeworth expansions for sums of independent random variables is given in [P]. See also [F], Chapt. XVI for a brief and very smooth introduction to the theory of Edgeworth expansions. The case of sums of independent random vectors is treated in [BR]. Extensions to statistics of a more complicated structure, such as 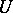-statistics — which are especially of interest in statistical theory — were studied by many authors over the last 15 years (as of 1988). An important recent contribution in this area is [BGZ].

References[edit]

[P]	V.V. Petrov, "Sums of independent random variables", Springer (1975) (Translated from Russian) MR0388499 Zbl 0322.60043 Zbl 0322.60042
[F]	W. Feller, "An introduction to probability theory and its applications", 2, Wiley (1971) pp. 135
[BR]	R.N. Bhattacharya, R. Ranga Rao, "Normal approximations and asymptotic expansions", Wiley (1976) MR0436272
[BGZ]	P.J. Bickel, F. Götze, W.R. van Zwet, "The Edgeworth expansion for 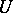-statistics of degree two" Ann. Statist., 14 (1986) pp. 1463–1484 MR868312