First fundamental form
 From Encyclopedia of Mathematics - Reading time: 3 min
From Encyclopedia of Mathematics - Reading time: 3 min
metric form, of a surface
A quadratic form in the differentials of the coordinates on the surface that determines the intrinsic geometry of the surface in a neighbourhood of a given point.
Let the surface be defined by the equation
$$ \mathbf r = \mathbf r ( u , v), $$
where $ u $ and $ v $ are coordinates on the surface, while
$$ d \mathbf r = \mathbf r _ {u} du + \mathbf r _ {v} dv $$
is the differential of the position vector $ \mathbf r $ along the chosen direction $ du :dv $ of displacement from a point $ M $ to an infinitesimally close point $ M ^ \prime $( see Fig. a).
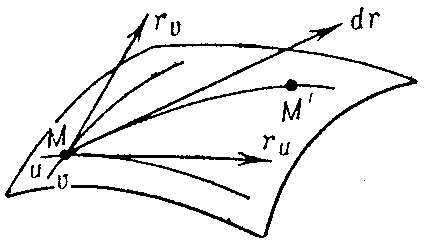
Figure: f040450a
The square of the principal linear part of the increment of the length of the arc $ MM ^ \prime $ can be expressed in terms of the square of the differential $ d \mathbf r $:
$$ \textrm{ I } = ds ^ {2} = d \mathbf r ^ {2} = \mathbf r _ {u} ^ {2} du ^ {2} + 2 \mathbf r _ {u} \mathbf r _ {v} du dv + \mathbf r _ {v} ^ {2} dv ^ {2} , $$
and is called the first fundamental form of the surface. The coefficients in the first fundamental form are usually denoted by
$$ E = \mathbf r _ {u} ^ {2} ,\ \ F = ( \mathbf r _ {u} , \mathbf r _ {v} ) ,\ \ G = \mathbf r _ {v} ^ {2} , $$
or, in tensor symbols,
$$ d \mathbf r ^ {2} = g _ {11} du ^ {2} + 2g _ {12} du dv + g _ {22} dv ^ {2} . $$
The tensor $ g _ {ij} $ is called the first fundamental, or metric, tensor of the surface. The first fundamental form is a positive-definite form at regular points on the surface:
$$ EG - F ^ { 2 } > 0. $$
The first fundamental form characterizes the metric properties of the surface: Knowledge of the first fundamental form enables one to calculate arc lengths on the surface:
$$ s = \int\limits _ {t _ {0} } ^ { t } \sqrt {E \left ( \frac{du}{dt} \right ) ^ {2} + 2F \frac{du}{dt} \frac{dv}{dt} + G \left ( \frac{dv}{dt} \right ) ^ {2} } dt, $$
where $ t $ is a parameter on the curve; angles between curves on the surface:
$$ \cos ( \widehat{ {dr \delta r }} ) = $$
$$ = \ \frac{E du \delta u + F( du \delta v+ dv \delta u)+ G dv \delta v }{\sqrt {E du ^ {2} + 2F du dv+ G dv ^ {2} } \sqrt {E \delta u ^ {2} + 2F \delta u \delta v+ G \delta v ^ {2} } } , $$
where $ du : dv $ and $ \delta u : \delta v $ are the directions of the tangent vectors to the curves (see Fig. b); and areas of regions on the surface:
$$ \sigma = \int\limits \int\limits \sqrt {EG - F ^ { 2 } } du dv . $$

Figure: f040450b
The form of the coefficients of the first fundamental form substantially depends on the choice of the coordinates. The first fundamental form has so-called orthogonal form
$$ E( u, v) du ^ {2} + G( u, v) dv ^ {2} $$
in orthogonal coordinates, canonical form
$$ du ^ {2} + G ^ {2} dv ^ {2} $$
in semi-geodesic coordinates, and isothermal (isometric) form in isothermal coordinates:
$$ ds ^ {2} = \lambda ^ {2} ( u, v)( du ^ {2} + dv ^ {2} ). $$
Sometimes a surface is characterized by special forms of the first fundamental form. For example, a Liouville surface is characterized by:
$$ [ \phi ( u) + \psi ( v)]( du ^ {2} + dv ^ {2} ). $$
The first fundamental form is a bending invariant for the surface: The Gaussian curvature at a given point can be calculated from the coefficients of the first fundamental form and their derivatives only (Gauss' theorem).
See Fundamental forms of a surface for the relation between the first fundamental form and other quadratic forms, as well as for literature.
Comments[edit]
In more current terminology the first fundamental form of an imbedded surface $ f: U \rightarrow \mathbf R ^ {3} $, $ U \subset \mathbf R ^ {2} $, is defined as follows. The inclusion $ ( Tf ) _ {u} ( \mathbf R _ {u} ^ {2} ) \subset T _ {f ( u) } \mathbf R ^ {3} $ defines a quadratic form on the tangent space $ ( Tf ) _ {u} ( \mathbf R _ {u} ^ {2} ) $ to the surface at $ f ( u) $ by restricting the canonical scalar product on $ T _ {f ( u) } \mathbf R ^ {3} \simeq \mathbf R ^ {3} $. Thus the first fundamental form of the surface $ f ( U) \subset \mathbf R ^ {3} $ simply assigns to a pair of tangent vectors $ X, Y $ to $ f ( U) $ at $ z \in f ( U) $ the inner product of $ X $ and $ Y $ in $ \mathbf R ^ {3} $.
Gauss' theorem is also known as the theorem egregium, cf. Gauss theorem.
The first fundamental form is also defined in higher (co)dimensions and for Riemannian spaces as ambient spaces (cf. [a1]–[a3]). In the last case it is given by the restriction of the Riemannian metric to the tangent subspaces defined by the given submanifold.
References[edit]
| [a1] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) MR0350630 Zbl 0264.53001 |
| [a2] | N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965) MR0179691 Zbl 0132.15104 |
| [a3] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1–2 , Interscience (1963–1969) MR1393941 MR1393940 MR0238225 MR1533559 MR0152974 Zbl 0526.53001 Zbl 0508.53002 Zbl 0175.48504 Zbl 0119.37502 |
| [a4] | C.C. Hsiung, "A first course in differential geometry" , Wiley (1981) pp. Chapt. 3, Sect. 4 MR0608028 Zbl 0458.53001 |
| [a5] | R.S. Millman, G.D. Parker, "Elements of differential geometry" , Prentice-Hall (1977) pp. 26 MR0442832 Zbl 0425.53001 |
 KSF
KSF