Geodesy, mathematical problems in

Problems involving the determination of the gravity field and the shape of the Earth in a unique coordinate system. The coordinates employed are the orthogonal Cartesian system $(x, y, z)$ and the curvilinear orthogonal coordinates $B, L, H$ [2] or $u, v, w$ , which are related to an oblate ellipsoid of revolution (on account of the resemblance between the Earth and such an ellipsoid). Here

$\begin{matrix} (1) & \begin{matrix} x = (N + H) \cos B \cos L, y = (N + H) \cos B \sin L, \\ z = (\frac{b^{2}}{a^{2}} N + H) \sin B, N = a {(1 - \frac{c^{2}}{a^{2}} \sin^{2} B)}^{-} 1 / 2, \end{matrix}} \end{matrix}$

where $a$ and $b$ are, respectively, the semi-major and semi-minor axes; $2 c$ is its focal distance;

$\begin{matrix} (2) & \begin{matrix} x = c \sin u \cos v \cosh w, \\ y = c \sin u \sin v \cosh w, \\ z = c \cos u \sinh w \end{matrix}} . \end{matrix}$

The shape and the field of the Earth are derived from geometric measurements (distances between points, angles between directions), measurements of the force of gravity, and observations of artificial satellites of the Earth.

Determinations of distances between observatories by very long base line (about thousands of kilometers) interferometry (VLBI) is the most accurate (about several centimeters) technique at present. A radiation of extra-galactic sources is observed. These determinations serve the purpose of establishing a coordinate system on Earth. When developing a network of angles on the Earth's surface, the elements of orientation of the local coordinate system must be specified.

Geodetic surveys without a plumb line play an important role in developing geodetic networks by extra-terrestrial data. Employment of the satellite global positioning system (GPS) is now (1988) the most promising way of carrying out this type of surveys. The accuracy of the system is about $\pm 2 cm$ at distances of $50 km$ [1], [5].

The general determination of the Earth's gravity field is based on satellite observations and special methods of celestial mechanics; namely, studies of artificial satellites are used to determine the difference between the Earth's gravity field and a spherical field. This is done, as a rule, by finding the expansion coefficients of the potential into a series of spherical functions, now up to the 180- or 360th degree and order. The methods of celestial mechanics are complemented by the theory of simultaneous determination of both the gravity field and the coordinates of the station from which satellites are tracked. The modern theory of determining the gravity field and shape of the Earth using gravimetric and geodesic measurements on the Earth's surface was established by M.S. Molodenskii [3], [4], [6]. It is based on solving a boundary value problem with an oblique derivative for the Laplace equation. The field of the attraction potential $U$ ,

$U = \frac{f m i}{c} Q_{0} (i \sinh w) + \frac{ω^{2} a^{2}}{3} \cdot \frac{Q_{2} (i \sinh w)}{Q_{2} (i b / c)} P_{2} (\cos u),$

close to that of the Earth may be used as a reference field. Here, $f$ is the gravitational constant, $m$ is a mass close to the mass of the Earth, $ω$ is the angular velocity of its rotation, and $P$ and $Q$ are the Legendre functions of the first and second kind, respectively. The gravitational potential $W$ is expressed in terms of its value $W_{0}$ at the zero of the altitude axis (sea level) and in terms of the increment, which is deducible from leveling and measurements of the force of gravity along its lines:

$W = W_{0} - \int g d h,$

where $d h$ is the elementary level increment in altitude. The increment $\int g d h$ of the potential is used to determine the approximate coordinate $w_{0}$ on the assumption that the leveling was carried out in the field of the potential $U$ . In order to make $w_{0}$ ( that is, the altitude $H$ ) more precise, and to determine the external gravity field of the Earth, it is sufficient to find the so-called distributing potential $T$ :

$\begin{matrix} (3) & T = W - Ω - U . \end{matrix}$

Here $Ω$ is the potential of the centrifugal force generated by the rotation of the Earth. The boundary condition on the surface of the Earth for finding the potential is obtained by using the relation $d W / d H = - g$ and by computing $d U / d w$ at the point with coordinate $w_{0}$ . At infinity ( $\sinh w \to \cosh w \to \infty$ ) the potential $T$ satisfies the condition $lim T = 0$ .

The solution of the problem is reduced to finding the density of a single layer on the Earth's surface as well, which is connected by some relation with the potential $T$ . This relation and this boundary condition yield a singular integral equation of the second kind. Under certain conditions the Fredholm alternative holds for this equation. For an ellipsoidal reference field the boundary conditions define a unique solution. If the reference field degenerates to a spherical field, any spherical function of the first degree becomes a solution of the problem. Owing to inevitable experimental errors, supplementary conditions are introduced — the coincidence of the centre of inertia of the Earth with the centre of the ellipsoid of reference, and parallelity of the principal polar central axis of inertia of the Earth and the minor axis of the ellipsoid of reference.

The centre of inertia of the Earth need not be situated on its axis of rotation. This will be the case, in particular, if from the gravity field of the Earth, in order to reduce the errors in gravity interpolation, the irregular effect of the topographical mass is removed. Practical numerical computations are difficult in mountainous regions, on account of the complexity of the Earth's surface.

The coordinates $B, L, H$ of a certain point, taken as the starting point in processing geometrical data, are initially fixed arbitrarily, but so that the components $ϕ - B, (λ - B) \cos B$ of deflection of the plumb line from the normal to the ellipsoid are small. It is assumed at the same time that the axis of rotation of the Earth and the ellipsoid axis are parallel, and that the planes of the initial astronomical and geodetic meridians are parallel as well.

The value of $W_{0}$ and the coordinates of the centre of inertia of the Earth are found by combining the solution of the above integral equation with the observed astronomical latitudes $ϕ$ and longitudes $λ$ and with the altitudes $H$ in the course of astronomic-gravimetric leveling.

The fundamental principles of the mathematical theory of the shape of the Earth were established by I. Newton (1687), who computed the oblateness of the ellipsoid shape of the Earth on the assumption that its density was uniform. A. Clairaut (1743) carried out a first-approximation study of the gravity field of an inhomogeneous Earth, rotating in a hydrostatic equilibrium. L. Euler in 1757 established the fundamental principles of the theory of level surfaces of the Earth's potential. P. Laplace (1785), who studied the attraction of celestial bodies — spheroids, in particular ellipsoids of rotation — generalized the results of Clairaut on the distribution of the order of the force of gravity on the surface of our planet, without using the assumption of hydrostatic equilibrium and preserving the accuracy of the proof of Clairaut (the oblateness of the Earth is of the order of 1:300). Moreover, Laplace developed the theory of spherical functions and spherical series. The studies of G. Stokes (1849), which were subsequently developed and completed by numerous geodetists, served as the theoretical basis of gravimetric measurements in geodesy prior to the appearance of the studies of Molodenskii. Stokes was the first to approach the problem of the determination of the shape of the Earth as a boundary value problem, and gave an approximate solution to the first boundary value problem for a spheroid, while substantiating the results of Clairaut and Laplace. Stokes' solution predetermined the results of P. Dirichlet, who in 1852 solved a similar problem for a sphere by expansion into spherical functions. Stokes also expressed the altitude of the external level surface of the planet over a spheroid in terms of the force of gravity on the surface of the planet. That it is possible to replace the attraction of a body by the attraction of a single layer on its surface was proved in 1840 by C.F. Gauss. The theory of rotation of an inhomogeneous liquid in a hydrostatic equilibrium is of importance for the simultaneous solutions of geophysical and geodesic problems. The principal results in this field must be credited to A.M. Lyapunov, L. Lichtenstein and S. Chandrasekhar.

References[edit]

[1]	Y., et al. Bock, "A demonstration of 1–2 parts in 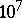accuracy using GPS" Bulletin Géodésique , 60 (1986) pp. 241–254
[2]	A. Möhle, "Die Verwendung von geographischen Koordinaten in der Theorie allgemeiner Flächen" , Friedrich-Wilhelm Univ. Bonn (1934) (Dissertation)
[3]	M.S. Molodenskii, V.F. Eremeev, M.I. Yurkina, "Methods for study of the external gravitational field and figure of the Earth" , Israel Program Sci. Transl. (1962) (Translated from Russian)
[4]	H. Moritz, "Advanced physical geodesy" , H. Wichmann , Karlsruhe (1980)
[5]	W.J. Senus, "NAVSTAR Global Positioning System: status" , The future of terrestrial and space methods for positioning. Proc. Internat. Assoc. Geodesy and Geophysics. XVIII General Assembly. Hamburg, August 15–27 , Ohio State Univ. (1983) pp. 181–445
[6]	Vaniček, E.J. Krakiwsky, "Geodesy: the concepts" , North-Holland (1982)

Comments[edit]

References[edit]

[a1]	H. Jeffreys, "The Earth, its origin, history and physical constitution" , Cambridge Univ. Press (1970)