Imbedding theorems

Theorems concerning a kind of problems involved in the study of inequalities between the norms of the same function in different classes (normed spaces). One is usually concerned with two classes $\mathfrak{M}$ and ${\mathfrak{M}}_1$, where $\mathfrak{M}$ is a part of ${\mathfrak{M}}_1$ ($\mathfrak{M}\subset {\mathfrak{M}}_1$), such that an inequality

$$\Vert f{\Vert }_{{\mathfrak{M}}_1}\le C\Vert f{\Vert }_{\mathfrak{M}}$$

is satisfied for all $f\in \mathfrak{M}$, where $C$ is a constant which is independent of $f$, and $\Vert \cdot {\Vert }_{\mathfrak{M}}$, $\Vert \cdot {\Vert }_{{\mathfrak{M}}_1}$ are the norms in $\mathfrak{M}$ and ${\mathfrak{M}}_1$, respectively. Under these conditions one speaks of an imbedding of $\mathfrak{M}$ into ${\mathfrak{M}}_1$ or one says that $\mathfrak{M}$ is imbeddable in ${\mathfrak{M}}_1$, written as $\mathfrak{M}\to {\mathfrak{M}}_1$ (cf. also Imbedding of function spaces). The studies connected with imbedding theorems constitute a branch of the theory of functions, but their main paths of development concern the boundary value problems of mathematical physics, in particular direct variational methods. For this reason a systematic theory of imbeddings of classes of differentiable functions of several variables has been developed during the past three decades.

The following problems are examples of problems solved by imbedding theorems. Let a function $f$ be known to have, usually generalized (cf. Generalized derivative), partial derivatives of order $l$ whose $p$-th powers are integrable on a given domain $\mathrm{\Omega }$ of the $n$-dimensional space ${\mathbf{R}}^n$. The questions are: 1) How many continuous derivatives does this function have on $\mathrm{\Omega }$? 2) If the domain $\mathrm{\Omega }$ has a sufficiently smooth boundary $\mathrm{\Gamma }$, is it possible to determine in some sense the trace $\varphi (x)$ of the function $f$ at the points $x\in \mathrm{\Gamma }$, i.e. the limit values of $f(u)$ as $u$ tends to $x$, and what are the differentiability properties of this trace? Such properties should often be known exactly enough such that a function $\varphi$ given on $\mathrm{\Gamma }$ and possessing these properties can be extended from $\mathrm{\Gamma }$ to $\mathrm{\Omega }$ in such a way that the extended function has generalized derivatives of order $l$ whose $p$-th powers are integrable on $\mathrm{\Omega }$. It will be seen from the facts given below that these limits (in the sense of almost-everywhere convergence) for the determination of the trace $\varphi$ of $f$ and of the extension of $\varphi$ can be accompanied by inequalities between the norms of $f$ on $\mathrm{\Omega }$ and $\mathrm{\Gamma }$, which are used in the theory of boundary value problems.

The multi-dimensional theory of imbeddings of classes of differentiable functions originated in the 1930s in the studies of S.L. Sobolev in the context of problems in mathematical physics. He is to be credited with fundamental imbedding theorems for the classes $W_p^l(\mathrm{\Omega })$ (the Sobolev spaces, cf. Sobolev space) which play an important role in analysis. A function $f(x)=f(x_1\dots x_n)$ belongs to $W_p^l(\mathrm{\Omega })$, $1\le p\le \mathrm{\infty }$, $l=0,1\dots$ if it is defined on $\mathrm{\Omega }$ and has a finite norm

$$\begin{array}{}\text{(1)}& \Vert f{\Vert }_{W_p^l(\mathrm{\Omega })}=\Vert f{\Vert }_{L_p(\mathrm{\Omega })}+\Vert f{\Vert }_{w_p^l(\mathrm{\Omega })},\end{array}$$

where

$$\begin{array}{}\text{(2)}& \begin{array}{c}\Vert f{\Vert }_{L_p(\mathrm{\Omega })}={(\underset{\mathrm{\Omega }}{\int }|f(x){|}^{p}dx)}^{1/p},\\ \Vert f{\Vert }_{w_p^l(\mathrm{\Omega })}=\sum _{|\mathbf{k}|=l}\Vert D^{\mathbf{k}}f{\Vert }_{L_p(\mathrm{\Omega })},\end{array}\}\end{array}$$

and the sum is extended over all possible (Sobolev-generalized) partial derivatives

$$\begin{array}{}\text{(3)}& D^{\mathbf{k}}f=\frac{{\partial }^{|\mathbf{k}|}f}{\partial x_1^{k_1}\dots \partial x_n^{k_n}},\end{array}$$

$$\mathbf{k}=(k_1\dots k_n),|\mathbf{k}|=\sum _{j=1}^n{k}_j,$$

of order $|\mathbf{k}|=l$.

Sobolev's fundamental theorem (with completions by V.I. Kondrashov and V.P. Il'in) for the case $\mathrm{\Omega }={\mathbf{R}}^n$: If $1\le m\le n$, $1<p<q<\mathrm{\infty }$, $0\le k=l-n/p+m/q$, the following imbedding is valid:

$$\begin{array}{}\text{(4)}& W_p^l({\mathbf{R}}^n)\to W_q^{[k]}({\mathbf{R}}^m),\end{array}$$

where $[k]$ is the integer part of $k$.

If $m<n$, this means that a function $f\in W_p^l({\mathbf{R}}^n)$ has a trace (see below) on any coordinate hyperplane ${\mathbf{R}}^m$ of dimension $m$,

$${f|}_{{\mathbf{R}}^m}=\varphi \in W_q^{[k]}({\mathbf{R}}^m)$$

and

$$\Vert f{\Vert }_{W_q^{[k]}({\mathbf{R}}^m)}\le C\Vert f{\Vert }_{W_p^l({\mathbf{R}}^n)},$$

where $C$ does not depend on $f$[6], [7].

A function $f$ defined on ${\mathbf{R}}^n$ has a trace on ${\mathbf{R}}^m$, where ${\mathbf{R}}^m$ is an $m$-dimensional (coordinate) subspace of points $\mathbf{x}=(x_1\dots x_m,x_{m+1}^0\dots x_n^0)$ with fixed $x_{m+1}^0\dots x_n^0$, if $f$ can be modified on some set of $n$-dimensional measure zero, so that

$$\begin{array}{}\text{(5)}& \Vert f(x_1\dots x_m,x_{m+1}^0\dots x_n^0)-\end{array}$$

$$-f(x_1\dots x_m,x_{m+1}\dots x_n){\Vert }_{L_p({\mathbf{R}}^m)}\to 0,$$

$$x_j\to x_j^0(j=m+1\dots n),$$

holds for the modified function (which is again denoted by $f$).

If $\mathfrak{M}$ is a set of functions $f$ defined on ${\mathbf{R}}^n$, the problem of describing the properties of the traces of these functions on a subspace ${\mathbf{R}}^m$ ($1\le m<n$) is said to be the trace problem for the class $\mathfrak{M}$.

Theorem (4) is a final theorem in terms of the classes $W_p^l(\mathrm{\Omega })$. Its further strengthening is possible only if new classes are introduced.

In the one-dimensional case $n=m=1$, where the trace problem does not occur, theorem (4) is due to G.H. Hardy and J.E. Littlewood.

The next stages in the development of this theory were Nikol'skii's imbedding theorems for generalized Hölder classes (cf. Hölder space) ( $H$-classes). These classes form a scale with continuously varying parameters which characterize the smoothness of the functions. They are anisotropic in the sense that their functions usually display different differentiability properties in different directions. Let ${\mathrm{\Omega }}_{\eta }$ be the set of points $\mathbf{x}\in \mathrm{\Omega }$ at distance from the boundary of $\mathrm{\Omega }$ greater than $\eta >0$, and let $\mathbf{r}=(r_1\dots r_n)$ be a positive vector ( $r_j>0$; $j=1\dots n$), $r_j=r_j^{\ast }+{\alpha }_j$, where $r_j^{\ast }$ is an integer and $0<{\alpha }_j\le 1$.

A function $f$ belongs to the class $H_p^{\mathbf{r}}(\mathrm{\Omega })$, $1\le p\le \mathrm{\infty }$, if $f\in L_p(\mathrm{\Omega })$ and if for an arbitrary $j=1\dots m$ a generalized partial derivative

$$\begin{array}{}\text{(6)}& D_j^{r_j^{\ast }}f=\frac{{\partial }^{r_j^{\ast }}f}{\partial x_j^{r_j^{\ast }}}\end{array}$$

exists which satisfies the inequality

$$\begin{array}{}\text{(7)}& {\Vert {\mathrm{\Delta }}_{jh}^2\left(D_j^{r_j^{\ast }}f\right)\Vert }_{L_p({\mathrm{\Omega }}_{2h}^{\prime })}\le M|h{|}^{{\alpha }_j},\end{array}$$

where ${\mathrm{\Delta }}_{jh}^2$ denotes the second-difference operator of the function with respect to the variable $x_j$, with step $h$, and $M$ is a constant which is independent of $h$.

The class $H_p^{\mathbf{r}}(\mathrm{\Omega })$ forms a Banach space with norm

$$\Vert f{\Vert }_{H_p^{\mathbf{r}}(\mathrm{\Omega })}=\Vert f{\Vert }_{L_p(\mathrm{\Omega })}+M_f,$$

where $M_f$ is the smallest constant $M$ for which the inequalities (7) are satisfied. If $r_1=\cdots =r_n=r$, the respective (isotropic) class is denoted by $H_p^r$. If $l$ is an integer, the class $H_p^l$ is close to the Sobolev class $W_p^l$, with an accuracy of $ϵ>0$, in the sense that

$$\begin{array}{}\text{(8)}& H_p^{l+ϵ}({\mathbf{R}}^n)\to W_p^l({\mathbf{R}}^n)\to H_p^{l-ϵ}({\mathbf{R}}^n).\end{array}$$

Nikol'skii's imbedding theorems are valid:

$$\begin{array}{}\text{(9)}& H_p^{\mathbf{r}}({\mathbf{R}}^n)\to H_q^{\rho \rho }({\mathbf{R}}^m),\end{array}$$

where

$$1\le p\le q\le \mathrm{\infty },1\le m\le n,\rho \rho =({\rho }_1\dots {\rho }_m),$$

$${\rho }_j=\kappa r_j(j=1\dots m),$$

$$\kappa =1-(\frac{1}{p}-\frac{1}{q})\sum _{j=1}^m{\frac{1}{r}}_j-\frac{1}{p}\sum _{j=m+1}^n{\frac{1}{r}}_j>0;$$

$$\begin{array}{}\text{(10)}& H_p^{\mathbf{r}}({\mathbf{R}}^n)\rightleftarrows H_p^{\rho \rho }({\mathbf{R}}^m),\end{array}$$

where $1\le p\le \mathrm{\infty }$, $1\le m<n$, ${\rho }_j=\kappa r_j$, $j=1\dots m,$

$$\kappa =1-\frac{1}{p}\sum _{j=m+1}^n{\frac{1}{r}}_j>0$$

(cf. [5]).

Theorem (9) is the anisotropic analogue of theorem (4), with the advantage that the (vectorial) superscripts $\mathbf{r},\rho \rho$ of the classes appearing in it may vary in a continuous manner. Moreover, it includes the cases $p=1,\mathrm{\infty }$. However, for $\kappa =0$ it is not valid, unlike (4). Hardy and Littlewood demonstrated the theorem for the one-variable case $(n=m=1)$ with non-integer $r$ and $\rho$.

The imbedding (10) with the upper arrow is also given by a special case of theorem (9), when $p=q$. It states that a function $f\in H_p^r({\mathbf{R}}^n)$ has a trace $f{\mid }_{{\mathbf{R}}^m}=\varphi$ on ${\mathbf{R}}^m$ and that also

$$\begin{array}{}\text{(11)}& \Vert \varphi {\Vert }_{H_p^{\rho }({\mathbf{R}}^m)}\le C\Vert f{\Vert }_{H_p^r({\mathbf{R}}^n)},\end{array}$$

where $C$ is independent of $f$. The reverse statement, symbolized by the lower arrow, is also true, and should be understood in the following sense: Any function $\varphi \in H_p^{\rho \rho }({\mathbf{R}}^m)$ defined on ${\mathbf{R}}^m$ may be extended to the entire space ${\mathbf{R}}^n$ so that the resulting function $f(\mathbf{x})$( with trace on ${\mathbf{R}}^m$ equal to $\varphi$) belongs to $H_p^{\mathbf{r}}({\mathbf{R}}^n)$ and satisfies the inequality (reverse to (11)):

$$\Vert f{\Vert }_{H_p^{\mathbf{r}}({\mathbf{R}}^n)}\le C\Vert \varphi {\Vert }_{H_p^{\rho \rho }({\mathbf{R}}^m)},$$

where $C$ does not depend on $\varphi$.

The mutually inverse imbeddings (10) represent a complete solution to the trace problem for $H$- classes, in terms of these classes.

Theorem (9) is transitive, which means that the transition

$$\begin{array}{}\text{(12)}& H_p^{\mathbf{r}}({\mathbf{R}}^n)\to H_{p^{\prime }}^{\rho {\rho }^{\prime }}({\mathbf{R}}^m)\to H_{p^{\prime \prime }}^{\rho {\rho }^{\prime \prime }}({\mathbf{R}}^{m^{\prime \prime }})\end{array}$$

from the first class in the chain (12) to the second, and then from the second to the third, where the parameters $\rho {\rho }^{\prime },\rho {\rho }^{\prime \prime }$ are computed by the formulas in (9), may be replaced by a direct transition from the first to the third class, $\rho {\rho }^{\prime \prime }$ being calculated by the same formulas.

Subsequently (cf. [14]) a solution was given for the trace problem in $W$- classes, which are in general anisotropic. This resulted in the introduction of a new family of classes of differentiable functions of several variables, $B_{p\theta }^{\mathbf{r}}({\mathbf{R}}^n)$, which depend on the vector parameter $\mathbf{r}$ and on two scalar parameters $p,\theta$ which satisfy the inequalities $1\le p,\theta \le \mathrm{\infty }$. This family was completely determined by O.V. Besov, who also studied its fundamental properties.

A function $f$ belongs to the class $W_p^{\mathbf{l}}(\mathrm{\Omega })$, where $\mathbf{l}=(l_1\dots l_n)$ is an integer vector, if it has finite meaningful norm

$$\begin{array}{}\text{(13)}& \Vert f{\Vert }_{W_p^{\mathbf{l}}(\mathrm{\Omega })}=\Vert f{\Vert }_{L_p(\mathrm{\Omega })}+\Vert f{\Vert }_{w_p^{\mathbf{l}}(\mathrm{\Omega })},\end{array}$$

$$\Vert f{\Vert }_{w_p^{\mathbf{l}}(\mathrm{\Omega })}=\sum _{j=1}^n\Vert D_j^{l_j}f{\Vert }_{L_p(\mathrm{\Omega })}.$$

A function $f$ belongs to the class $B_{p\theta }^{\mathbf{r}}(\mathrm{\Omega })$, where $\mathbf{r}=(r_1\dots r_n)$ is an arbitrary, not necessarily integer, vector, $1\le p,\theta \le \mathrm{\infty }$, $r_j>0$, if it has finite norm

$$\Vert f{\Vert }_{B_p^{\mathbf{r}}(\mathrm{\Omega })}=\Vert f{\Vert }_{L_p(\mathrm{\Omega })}+\Vert f{\Vert }_{b_p^{\mathbf{r}}(\mathrm{\Omega })},$$

$$\Vert f{\Vert }_{b_p^{\mathbf{r}}(\mathrm{\Omega })}=\sum _{j=1}^n{\{\underset{0}{\overset{\mathrm{\infty }}{\int }}{t}^{-\theta {\alpha }_j-1}\Vert {\mathrm{\Delta }}_{jt}^2{f}_{x_j}^{(r_j^{\ast })}{\Vert }_{L_p({\mathrm{\Omega }}_{2t})}^{\theta }dt\}}^{1/\theta },$$

where the numbers $r_j^{\ast }$ and ${\alpha }_j$ were defined above.

It is natural to regard the class $B_{p\theta }^{\mathbf{r}}$ if $\theta =\mathrm{\infty }$ as identical with the class $H_p^{\mathbf{r}}$( $B_{p\mathrm{\infty }}^{\mathbf{r}}=H_p^{\mathbf{r}}$). One usually writes $B_{p\theta }^r$ rather than $B_{p\theta }^{\mathbf{r}}$ if $r_1=\cdots =r_n=r$ and $B_p^{\mathbf{r}}=B_{pp}^{\mathbf{r}}$, $B_p^r=B_{pp}^r$. The classes $B_{p\theta }^{\mathbf{r}}$ are Banach spaces for any given $p,\theta ,\mathbf{r}$.

The imbedding theorems (9) and (10) are valid if the symbols $H$ in them are replaced by $B$. There also exist a mutually inverse imbedding:

$$\begin{array}{}\text{(14)}& W_p^{\mathbf{r}}({\mathbf{R}}^n)\rightleftarrows B_p^{\kappa {\mathbf{r}}^m}({\mathbf{R}}^m),\end{array}$$

where $\mathbf{r}$ is an integer, $1<p<\mathrm{\infty }$, ${\mathbf{r}}^m=(r_1\dots r_m,0\dots 0)$, $\kappa =1-(1/p)\sum _{j=}m+1^{n}1/r_j>0$, which completely solves the trace problem for $W$- classes, and does not interfere with mutually inverse imbeddings, completely expressed in the language of $B$- classes:

$$\begin{array}{}\text{(15)}& B_{p\theta }^{\mathbf{r}}({\mathbf{R}}^n)\rightleftarrows B_{p\theta }^{\kappa {\mathbf{r}}^m}({\mathbf{R}}^m).\end{array}$$

The classes $B_2^{\mathbf{r}}$ corresponding to the parameter values $p=\theta =2$ are usually denoted by $W_2^{\mathbf{r}}$( $B_2^{\mathbf{r}}=W_2^{\mathbf{r}}$). If $p=2$, the imbeddings (14) may also be written as

$$\begin{array}{}\text{(16)}& W_2^{\mathbf{r}}({\mathbf{R}}^n)\rightleftarrows W_2^{\kappa {\mathbf{r}}^m}({\mathbf{R}}^m).\end{array}$$

Classes whose definition involves the concept of a Liouville fractional derivative (cf. Fractional integration and differentiation) are natural extensions of $W$- classes.

Using the terminology of generalized functions (cf. Generalized function), it is possible to define a class $\mathrm{\Lambda }$ of test functions such that the class ${\mathrm{\Lambda }}^{\prime }$ of generalized functions constructed over it will have the following properties: 1) $L_p({\mathbf{R}}^n)\subset {\mathrm{\Lambda }}^{\prime }$ for any finite $p\ge 0$; 2) for any $l>0$, not necessarily an integer, the operation

$$\begin{array}{}\text{(17)}& D_j^{l}f=x_j^{l_j}\tilde{f}hat,f\in {\mathrm{\Lambda }}^{\prime },\end{array}$$

where $\tilde{\psi },\hat{\psi }$ denote, respectively, the direct and the inverse Fourier transform of $\psi \in {\mathrm{\Lambda }}^{\prime }$, is meaningful; and 3) if $l$ is an integer and the function $f\in L_p({\mathbf{R}}^n)$ has a Sobolev-generalized derivative $D_j^{l}f\in L_p({\mathbf{R}}^n)$, then equation (17) applies to it.

In case $l$ is a fraction, operation (17) on infinitely-differentiable functions of compact support is identical with the Liouville fractional differentiation operation. It is natural to call $D_j^{l}f$ the fractional derivative of $f$ of order $l$ with respect to $x_j$ if $l$ is not an integer.

If an arbitrary vector $\mathbf{l}=(l_1\dots l_n)$ is given, one may introduce the space $L_p^{\mathbf{l}}({\mathbf{R}}^n)$, $1\le p<\mathrm{\infty }$, which is identical with $W_p^{\mathbf{l}}({\mathbf{R}}^n)$ for integer $\mathbf{l}$, by replacing $W$ in (13) by $L$.

If $l=l_1=\cdots =l_n$, one puts $L_p^l=L_p^{\mathbf{l}}$. The family of classes $L_p^{\mathbf{l}}({\mathbf{R}}^n)$, $\mathbf{l}>0$, $1\le p<\mathrm{\infty }$, may be regarded as a natural extension of the family $W_p^{\mathbf{l}}({\mathbf{R}}^n)$ to fractional $\mathbf{l}$— "natural" , since from the point of view of the present circle of interest the classes $L_p^{\mathbf{l}}$ display "all the advantages and all the drawbacks of Wpl" . If $L$ is substituted for $W$ in formula (4) (where $k$ may be substituted for $[k]$) or in (8) (where $l$ may be a fraction) or in (14), (16) (where $\mathbf{r}$ may be a fraction), these formulas will remain valid. The same also applies to formula (9) if $H$ is replaced by $L$, even under the wider condition $\kappa \ge 0$, but under the assumption that $1<p<q<\mathrm{\infty }$.

In what follows the apparatus of generalized functions will be used, except that these now constitute the space $S^{\prime }$. For any real number $\rho$ the Bessel–Macdonald operation is meaningful:

$$J_{\rho }f=(1+|\mathbf{x}{|}^2{)}^{-\rho /2}\tilde{f}hat,f\in S^{\prime },|\mathbf{x}{|}^2=\sum _{j=1}^n{x}_j^2.$$

It has the following properties: $J_{0}f=f$, $J_{r+\rho }=J_r{J}_{\rho }$, $J_{-}2l=(1-\mathrm{\Delta }{)}^l$, $l=0,1\dots$ where $\mathrm{\Delta }=\sum _{j=}{1}^n{\partial }^2/\partial x_j^2$ is the Laplace operator.

The isotropic class $L_p^{\rho }=L_p^{\rho }({\mathbf{R}}^n)$, $1<p<\mathrm{\infty }$, may also be defined as the set of functions $f$ that can be represented in the form $f=J_{\rho }\varphi$ where the functions $\varphi$ run through the space $L_p=L_p({\mathbf{R}}^n)$( $L_p^{\rho }=J_{\rho }(L_p)$); moreover, up to equivalence,

$$\Vert f{\Vert }_{L_p^{\rho }}=\Vert \varphi {\Vert }_{L_p}.$$

This definition of the class $L_p^{\rho }$ is also suitable for negative $\rho$, but in such a case $L_p^{\rho }$ is a set of (usually generalized) functions $(L_p^{\rho }\subset S^{\prime })$. In particular, $L_p^0=L_p$.

The operation $J_{\rho }$ may also be employed as a tool in defining the classes $B_{p\theta }^r$( $B_{p\mathrm{\infty }}^r=H_p^r$). To do this, one calls a generalized function $f$ regular in the sense of $L_p$ or belonging to $S_p^{\prime }$ if there exists a $\rho >0$ such that $J_{\rho }f\in L_p$. Any function $f\in B_{p\theta }^r=B_{p\theta }^r({\mathbf{R}}^n)$, $1\le \rho ,\theta \le \mathrm{\infty }$, $B_{p\mathrm{\infty }}^r=H_p^r$, can be defined as a function that is regular in the sense of $L_p$ and that can be represented as a series

$$f(\mathbf{x})=\sum _{s=0}^{\mathrm{\infty }}{q}_s(\mathbf{x}),$$

weakly converging towards $f$( in the sense of $S^{\prime }$), where $q_0$ has spectrum (the support of ${\tilde{q}}_0$) in ${\mathrm{\Delta }}_0$, while $q_s$, $s\ge 1$, has spectrum in ${\mathrm{\Delta }}_{s+1}\setminus {\mathrm{\Delta }}_{s-1}$ and

$${\mathrm{\Delta }}_s=\{\mathbf{x}:|x_j|\le 2^s;j=1\dots n\},$$

and also

$$\Vert f{\Vert }_{B_{p\theta }^r}={(\sum _{s=0}^{\mathrm{\infty }}{2}^{s\theta r}\Vert q_s{\Vert }_{L_p}^{\theta })}^{1/\theta }<\mathrm{\infty }.$$

In particular,

$$\Vert f{\Vert }_{H_p^r}=\Vert f{\Vert }_{B_{p\mathrm{\infty }}^r}=\underset{s}{sup}(2^{sr}\Vert q_s{\Vert }_{L_p}).$$

This definition of the class $B_{p\theta }^r$ is automatically extended to the case $r\le 0$, and the functions $f$ belonging to classes with negative $r$ will usually be generalized $(f\in S^{\prime })$. Here, $J_r(B_p^0)=B_p^r$, $-\mathrm{\infty }<r<\mathrm{\infty }$.

There also exist other, equivalent, definitions of the negative classes $B_{p\theta }^r$, based on the principle of interpolation of function spaces. The definition given above is constructive — each class defined by the parameters $r,p,\theta$ is defined independently, and it is possible to define constructively linear operations with the aid of which a function $q_s$( of exponential type $2^{s+}1$ if $s\ge 1$ and of type 1 if $s=0$) is defined in terms of a given function $f\in S_p^{\prime }$.

The following imbedding theorem is valid:

$${\mathrm{\Lambda }}_p^r({\mathbf{R}}^n)\to {\mathrm{\Lambda }}_q^{r-(1/p-1/q)n}({\mathbf{R}}^n).$$

This theorem is of the same type as theorem (4), but with $n=m$; it is valid for all real $r$ for $\mathrm{\Lambda }=L$, $1<p<q<\mathrm{\infty }$, or for $\mathrm{\Lambda }=B$, $1\le p<q<\mathrm{\infty }$, $1\le \theta <\mathrm{\infty }$, or for $\mathrm{\Lambda }=H$, $1\le p<q\le \mathrm{\infty }$.

On the other hand, for $r-(n-m)/p=0$, an arbitrary function $f\in {\mathrm{\Lambda }}_p^r({\mathbf{R}}^n)$ usually has no trace on ${\mathbf{R}}^m$( $m<n$) unless additional conditions are imposed.

The imbedding theorems formulated above apply to classes of functions defined on the entire $n$- dimensional space ${\mathbf{R}}^n$[5]. In practical applications, however, it is important to have similar theorems for domains $\mathrm{\Omega }\subset {\mathbf{R}}^n$ which should be as general as possible. The geometrical structure of the domains $\mathrm{\Omega }$ for which the above imbedding theorems are valid for the classes $W$, $B$ and $H$, where ${\mathbf{R}}^n$, ${\mathbf{R}}^m$ must be replaced, respectively, by $\mathrm{\Omega }$, ${\mathbf{R}}^m\cap \mathrm{\Omega }$, has now been clarified. For the isotropic classes $W_p^r(\mathrm{\Omega })$, $B_{p\theta }^r(\mathrm{\Omega })$ the domain $\mathrm{\Omega }$ must satisfy a cone condition or, which is equivalent to it, its boundary must locally satisfy a Lipschitz condition. For the anisotropic classes $W_p^{\mathbf{r}}(\mathrm{\Omega })$, $B_{p\theta }^{\mathbf{r}}(\mathrm{\Omega })$ the domain $\mathrm{\Omega }$ must satisfy an $\mathbf{r}$- horn condition or a bent cone condition, and this condition is, in a certain sense, necessary [2].

Another problem with important practical applications is the trace problem on $m$- dimensional manifolds $S^m$.

This problem has been completely solved for the isotropic classes $W$, $H$, $B$( see [2], ). If $S^m$ is sufficiently differentiable and $r=r_1=\cdots =r_n$, $S^m$ can be substituted for ${\mathbf{R}}^m$ in (14), (15) and (16), and $B$ can be substituted for $H$ in . If $S^m$ is piecewise smooth the problem has also been solved completely , [22]. The conditions for the solution of the problem are expressed by mutually inverse imbeddings on individual smooth pieces of $S^m$ on one hand, and, on the other hand, by special additional conditions on the behaviour of the functions of the respective classes at the points of contact of these smooth pieces. The solution of the trace problem for anisotropic classes [9], [21] is also in an advanced stage. Here major difficulties arise, concerning the characteristics of the trace at the points of $S^m$ where the tangent planes to $S^m$ are parallel to the coordinate axes.

One more problem follows. Given a function

$$f\in {\mathrm{\Lambda }}_p^{\mathbf{r}}({\mathbf{R}}^n)={\mathrm{\Lambda }}_p^{\mathbf{r}},$$

where ${\mathrm{\Lambda }}_p^{\mathbf{r}}$ denotes one of the classes considered above. What mixed partial derivatives $D^{k}f$ does this function have and what are their properties? A positive answer to this question depends on the magnitude

$$\kappa =1-\sum _{j=1}^m\frac{k_j}{r_j}.$$

In fact, for $f\in {\mathrm{\Lambda }}_p^{\mathbf{r}}$ there exists a partial derivative $D^{\mathbf{k}}f$ which belongs to ${\mathrm{\Lambda }}_p^{\kappa \mathbf{r}}$ if $\kappa >0$. This condition may be generalized to the case of the spaces $L_p^{\mathbf{r}}$ if $\kappa \ge 0$( see [5]).

Yet follows another characteristic theorem, which may perhaps be called a theorem on weak compactness, and which has applications in the theory of direct methods of variational calculus.

Out of the infinite set $\mathfrak{M}$ of functions $f$ which satisfy the inequality

$$\Vert f{\Vert }_{{\mathrm{\Lambda }}_p^{\mathbf{r}}({\mathbf{R}}^n)}\le K,$$

where $K$ is a known constant and $\mathrm{\Lambda }$ is one of the classes discussed above, it is possible to separate a sequence $\{f_m\}$ of functions and to indicate a function $f_0$ with norm

$$\Vert f_0{\Vert }_{{\mathrm{\Lambda }}_p^{\mathbf{r}}({\mathbf{R}}^n)}\le K,$$

such that, for all bounded domains $G\subset {\mathbf{R}}^n$ and all vectors $ϵϵ>0$,

$$\Vert f_m-f_0{\Vert }_{{\mathrm{\Lambda }}_p^{\mathbf{r}-ϵϵ}(G)}\to 0,m\to \mathrm{\infty },$$

[5]. In this formulation ${\mathbf{R}}^n$ may be replaced by a domain $\mathrm{\Omega }$ if the latter has a sufficiently nice boundary. Only the typical function classes (and the imbedding theorems connected with them) which are most often encountered in practical applications were discussed above. In modern investigations stress is laid [2] on more general classes, in which more or less arbitrary differential operators play the role of the starting partial derivatives $D^{\mathbf{k}}f$, $D_j^{p}f$.

Other classes under study comprise the so-called weight classes (cf. Weight space), a typical example of which is the class $W_{p\alpha }^r(\mathrm{\Omega })$, defined as follows. Let $\rho (\mathbf{x})$ be the distance between a point $\mathbf{x}$ and the boundary $\mathrm{\Gamma }$ of a domain $\mathrm{\Omega }\subset {\mathbf{R}}^n$. A function $f$ belongs to $W_{p\alpha }^r(\mathrm{\Omega })$, $r>0$, $1\le p<\mathrm{\infty }$, if it has finite norm (see [4], [12])

$$\Vert f{\Vert }_{W_{p\alpha }^r(\mathrm{\Omega })}=\Vert f{\Vert }_{L_p(\mathrm{\Omega })}+\Vert f{\Vert }_{w_{p\alpha }^r(\mathrm{\Omega })},$$

where

$$\Vert f{\Vert }_{w_{p\alpha }^r(\mathrm{\Omega })}=\sum _{|\mathbf{k}|=r}{\Vert \frac{D^{\mathbf{k}}f}{{\rho }^{\alpha }}\Vert }_{L_p(\mathrm{\Omega })}.$$

One result is as follows. Let $\mathrm{\Gamma }$ be a sufficiently smooth boundary of dimension $m$; then

$$W_{p\alpha }^r(\mathrm{\Omega })\rightleftarrows H_p^{r+\alpha -(n-m)/p}(\mathrm{\Gamma }),$$

if $r+\alpha -(n-m)/p>0$, $\alpha <(n-m)/p$, $1<p<\mathrm{\infty }$.

Example. The use of imbedding theorems presents a complete solution of the problem of conditions on the boundary function under which the Dirichlet principle is applicable. In fact, take the partial derivatives in the generalized sense and assume, for the sake of simplicity, that the surface $\mathrm{\Gamma }$( the boundary of a three-dimensional domain) is bounded and is twice differentiable, and that a function $f_0\in W_2^1(\mathrm{\Omega })$ on $\mathrm{\Omega }$ has been given. For this function the Dirichlet integral $D(f_0)<\mathrm{\infty }$ and also, in accordance with the imbedding theorem

$$W_2^1(\mathrm{\Omega })\rightleftarrows W_2^{1/2}(\mathrm{\Gamma })=B_2^{1/2}(\mathrm{\Gamma }),$$

$f_0$ has a trace on $\mathrm{\Gamma }$( the fact that a trace of $f_0$ exists can be established with the aid of coarser imbedding theorems). Denoting by $\mathfrak{M}$ the class of functions $f\in W_2^1(\mathrm{\Omega })$ with the same trace on $\mathrm{\Gamma }$ as $f_0$, $f{|}_{\mathrm{\Gamma }}=f_0{|}_{\mathrm{\Gamma }}=\varphi$, the Dirichlet principle may be formulated as follows: The minimum of $D(f)$ over the functions $f\in \mathfrak{M}$ is attained for a unique function which is also harmonic on $\mathrm{\Omega }$. It follows from the imbedding theorem above that the Dirichlet principle is applicable if and only if the class $\mathfrak{M}$ is non-empty, i.e. when the boundary function $\varphi \in B_2^{1/2}(\mathrm{\Gamma })$.

In justifying the Dirichlet principle, the first step is to prove that the function $u\in \mathfrak{M}$ exists and is unique, and the fact that $u$ is a generalized solution of the Dirichlet problem. A special method is then used to successively establish that the generalized solution belongs to the classes $W_2^l(\omega )$, where $l=2,3\dots$ and $\omega \subset \mathrm{\Omega }$ is an arbitrary closed sphere. In particular, from the fact that $u\in W_2^4(\omega )$, applying the imbedding theorem

$$W_2^4(\omega )\to H_2^4(\omega )\to H_{\mathrm{\infty }}^{5/2}(\omega )$$

(cf. [2], [5]) for $n=m=3$, $p=2$, $q=\mathrm{\infty }$, $r_1=r_2=r_3=4$, one deduces that the function $u$ may be modified on a set of three-dimensional measure zero so that the function thus obtained is twice continuously differentiable on $\mathrm{\Omega }$. It can then readily be proved that $u$ is harmonic.

This example may be generalized to include certain functionals with partial derivatives of different orders, raised to a power usually distinct from 2 $(p\ne 2)$; it is then necessary to use imbedding theorems for more general, usually anisotropic, classes.

References[edit]

[1]	O.V. Besov, et al., "The theory of imbedding classes of differentiable functions of several variables" , Partial differential equations , Moscow (1970) pp. 38–63 (In Russian)
[2]	O.V. Besov, V.P. Il'in, S.M. Nikol'skii, "Integral representations of functions and imbedding theorems" , Wiley (1978) (Translated from Russian)
[3]	V.I. Burenkov, "Imbedding and extension theorems for classes of differentiable functions of several variables in the whole space" Itogi Nauk. Mat. Anal. 1965 (1966) (In Russian)
[4]	S.M. Nikol'skii, "On imbedding, continuation and approximation theorems for differentiable functions of several variables" Russian Math. Surveys , 16 : 5 (1961) pp. 55–104 Uspekhi Mat. Nauk , 16 : 5 (1961) pp. 63–114
[5]	S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian)
[6]	S.L. Sobolev, "Applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian)
[7]	S.L. Sobolev, "Introduction to the theory of cubature formulas" , Moscow (1974) (In Russian)
[8]	O.V. Besov, "Investigation of a class of function spaces in connection with imbedding and embedding theorems" Trudy Mat. Inst. Steklov. , 60 (1961) pp. 42–81 (In Russian)
[9]	Ya.S. Bugrov, "Boundary properties of functions of class 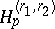on domains with corner points" Sibirsk. Mat. Zh. , 5 : 5 (1964) pp. 1007–1026 (In Russian)
[10]	V.P. Il'in, "On an inclusion theorem for a limiting exponent" Dokl. Akad. Nauk SSSR , 96 : 5 (1954) pp. 905–908 (In Russian)
[11]	V.I. Kondrashov, "Sur certaines propriétés des fonctions dans l'espace" Dokl. Akad. Nauk SSSR , 48 (1945) pp. 535–538
[12]	L.D. Kudryavtsev, "Direct and inverse imbedding theorems. Applications to solutions of elliptic equations by variational methods" Trudy Mat. Inst. Steklov. , 55 (1959) (In Russian)
[13]	P.I. Lizorkin, "Boundary properties of functions from "weight" classes" Soviet Math. Dokl. , 1 : 3 (1960) pp. 589–593 Dokl. Akad. Nauk SSSR , 132 : 3 (1960) pp. 514–517
[14]	P.I. Lizorkin, "Generalized Liouville differentiation and the function spaces 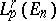. Imbedding theorems" Mat. Sb. , 60 (102) : 3 (1963) pp. 325–353 (In Russian)
[15]	S.M. Nikol'skii, "Inequalities for entire functions of finite degree and their application to the theory of differentiable functions in several variables" Trudy Mat. Inst. Steklov. , 38 (1951) pp. 244–278 (In Russian)
[16a]	S.M. Nikol'skii, "Properties of certain classes of functions of several variables on a differentiable manifold" Mat. Sb. , 33 (75) : 2 (1953) pp. 261–326 (In Russian)
[16b]	S.M. Nikol'skii, "Boundary properties of functions defined in a region with corner points" Mat. Sb. , 43 (85) : 1 (1957) pp. 127–144 (In Russian)
[17]	S.L. Sobolev, "Le problème de Cauchy dans l'espace des fonctionnelles" Dokl. Akad. Nauk SSSR , 3 : 7 (1935) pp. 291–294
[18a]	S.L. Sobolev, "A new method for solving the Cauchy problem for partial differential equations of normal hyperbolic type" Mat. Sb. , 1 (43) : 1 (1936) pp. 39–72 (In Russian)
[18b]	S.L. Sobolev, "On a theorem in functional analysis" Mat. Sb. , 4 (46) : 3 (1938) pp. 471–497 (In Russian) (French abstract)
[19]	L.N. Slobodetskii, "S.L. Sobolev's spaces of fractional order and their application to boundary value problems for partial differential equations" Dokl. Akad. Nauk SSSR , 118 : 2 (1958) pp. 243–246 (In Russian)
[20]	S.V. Uspenskii, "Imbedding theorems for classes with weights" Trudy Mat. Inst. Steklov. , 60 (1961) pp. 282–303 (In Russian)
[21]	S.V. Uspenskii, "Boundary properties of a class of differentiable funtions in smooth regions" Soviet Math. Dokl. , 6 : 5 (1965) pp. 1299–1302 Dokl. Akad. Nauk SSSR , 164 : 4 (1965) pp. 750–752
[22]	G.N. Yakovlev, "Boundary properties of a class of functions" Trudy Mat. Inst. Steklov. , 60 (1961) pp. 325–349 (In Russian)
[23]	E. Gagliardo, "Caratterizzazioni delle trace sulla frontiera relative ad alcune classi di funzioni in variabli" Rend. Sem. Mat. Univ. Padova , 27 (1957) pp. 284–305
[24]	G.H. Hardy, J.E. Littlewood, "A convergence criterion for Fourier series" Math. Z. , 28 (1928) pp. 612–634
[25]	J.L. Lions, E. Magenes, "Non-homogenous boundary value problems and applications" , 1–2 , Springer (1972) (Translated from French)