Polynomial convexity

Let $\mathcal{P}$ denote the set of holomorphic polynomials on ${\mathbf{C}}^n$ (cf. also Analytic function). Let $K$ be a compact set in ${\mathbf{C}}^n$ and let $\Vert P{\Vert }_K={\max }_{z\in K}|P(z)|$ be the sup-norm of $P\in \mathcal{P}$ on $K$. The set

$$\hat{K}=\{z\in {\mathbf{C}}^n:|P(z)|\le \Vert P{\Vert }_K,\mathrm{\forall }P\in \mathcal{P}\},$$

is called the polynomially convex hull of $K$. If $\hat{K}=K$ one says that $K$ is polynomially convex.

An up-to-date (as of 1998) text dealing with polynomial convexity is [a3], while [a13] and [a27] contain some sections on polynomial convexity, background and older results. The paper [a24] is an early study on polynomial convexity.

Polynomial convexity arises naturally in the context of function algebras (cf. also Algebra of functions): Let 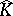$P(K)$ denote the uniform algebra generated by the holomorphic polynomials on $K$ with the sup-norm. The maximal ideal space $M$ of $P(K)$ is the set of homomorphisms mapping $P(K)$ onto $\mathbf{C}$, endowed with the topology inherited from the dual space $P(K{)}^{\ast }$. It can be identified with via

$$z\in \hat{K}\leftrightarrow m_z,$$

$$P\mapsto P(z),P\in \mathcal{P}.$$

Moreover, if $A$ is any finitely generated function algebra on a compact Hausdorff space, then $A$ is isomorphic to $P(K)$, where for $K$ one can take the joint spectrum of the generators of $A$ (cf. also Spectrum of an operator).

By the Riesz representation theorem (cf. Riesz theorem) there exists for every $z\in \hat{K}$ at least one representing measure ${\mu }_z$, that is, a probability measure ${\mu }_z$ on $K$ such that

$$P(z)=m_z(P)={\int }_{K}P(\zeta )d{\mu }_z(\zeta ),P\in \mathcal{P}.$$

One calls ${\mu }_z$ a Jensen measure if it has the stronger property

$$\log |P(z)|\le {\int }_K\log |P(\zeta )|d{\mu }_z(\zeta ),P\in \mathcal{P}.$$

It can be shown that for each $z\in \hat{K}$ there exists a Jensen measure ${\mu }_z$. See e.g. [a27].

For compact sets 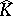$K$ in $\mathbf{C}$ one obtains by "filling in the holes" of $K$, that is, $\hat{K}=\mathbf{C}\mathrm{\setminus }{\mathrm{\Omega }}_{\mathrm{\infty }}$, where ${\mathrm{\Omega }}_{\mathrm{\infty }}$ is the unbounded component of $\mathbf{C}\mathrm{\setminus }K$. In ${\mathbf{C}}^n$, $n>1$, there is no such a simple topological description.

Early results on polynomial convexity, cf. [a13], are

Oka's theorem: If $K$ is a polynomially convex set in ${\mathbf{C}}^n$ and $f$ is holomorphic on a neighbourhood of $K$, then $f$ can be written on $K$ as a uniform limit of polynomials. Cf. also Oka theorems.

Browder's theorem: If $K$ is polynomially convex in ${\mathbf{C}}^n$, then $H^p(K,\mathbf{C})=0$ for $p\ge n$.

Here, $H^p(K,\mathbf{C})$ is the $p$th Čech cohomology group. More recently (1994), the following topological result was obtained, cf. [a9], [a3]:

Forstnerič' theorem: Let $K$ be a polynomially convex set in ${\mathbf{C}}^n$, $n\ge 2$. Then

$$H_k({\mathbf{C}}^n\mathrm{\setminus }K;G)=0,1\le k\le n-1,$$

and

$${\pi }_k({\mathbf{C}}^n\mathrm{\setminus }K)=0,1\le k\le n-1.$$

Here, $H_k(X,G)$ denotes the $k$th homology group of $X$ with coefficients in an Abelian group $G$ and ${\pi }_k(X)$ is the $k$th homotopy group of $X$.

One method to find 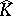is by means of analytic discs. Let $\mathrm{\Delta }$ be the unit disc in $\mathbf{C}$ and let $T$ be its boundary. An analytic disc is (the image of) a holomorphic mapping $f:\mathrm{\Delta }\to {\mathbf{C}}^n$ such that $f$ is continuous up to $T$. Similarly one defines an $H^{\mathrm{\infty }}$-disc as a bounded holomorphic mapping $f:\mathrm{\Delta }\to {\mathbf{C}}^n$. Its components are elements of the usual Hardy space $H^{\mathrm{\infty }}(\mathrm{\Delta })$ (cf. Hardy spaces).

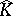Now, let $K$ be compact in ${\mathbf{C}}^n$ and suppose that $f(T)\subset K$ for some analytic disc $f$. Then $f(\mathrm{\Delta })\subset \hat{K}$ by the maximum principle applied to $P\circ f$ for polynomials $P\in \mathcal{P}$. The same goes for $H^{\mathrm{\infty }}$-discs whose boundary values are almost everywhere in $K$. One says that the disc $f$ is glued to $K$. Next, one says that has analytic structure at $p\in \hat{K}$ if there exists a non-constant analytic disc $f$ such that $f(0)=p$ and the image of $f$ is contained in .

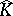It was a major question whether 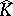$\hat{K}\mathrm{\setminus }K$ always has analytic structure. Moreover, when is obtained by glueing discs to $K$? One positive result in this direction is due to H. Alexander [a1]; a corollary of his work is as follows: If $K$ is a rectifiable curve in ${\mathbf{C}}^n$, then either $\hat{K}=K$ and $P(K)=C(K)$, or $\hat{K}\mathrm{\setminus }K$ is a pure $1$-dimensional analytic subset of ${\mathbf{C}}^n\mathrm{\setminus }K$ (cf. also Analytic set). If $K$ is a rectifiable arc, $K$ is polynomially convex and $P(K)=C(K)$.

See [a1] for the complete formulation. Alexander's result is an extension of pioneering work of J. Wermer, cf. [a30], E. Bishop and, later, G. Stolzenberg [a26], who dealt with real-analytic, respectively $C^1$, curves. Wermer [a29] gave the first example of an arc in ${\mathbf{C}}^3$ that is not polynomially convex, cf. [a3]. However, Gel'fand's problem (i.e., let $\gamma$ be an arc in ${\mathbf{C}}^n$ such that $\hat{\gamma }=\gamma$; is it true that $P(\gamma )=C(\gamma )$?) is still open (2000). Under the additional assumption that its projections into the complex coordinate planes have $2$-dimensional Hausdorff measure $0$, the answer is positive, see [a3].

F.R. Harvey and H.B. Lawson gave a generalization to higher-dimensional $K$, cf. [a12], which includes the following.

Let $p\ge 1$. If $K$ is a $C^2$ $(2p+1)$-dimensional submanifold of ${\mathbf{C}}^n$ and at each point of $K$ the tangent space to $K$ contains a $p$-dimensional complex subspace, then $K$ is the boundary of an analytic variety (in the sense of Stokes' theorem).

Another positive result is contained in the work of E. Bedford and W. Klingenberg, cf. [a4]: Suppose $\mathrm{\Gamma }\subset {\mathbf{C}}^2$ is the graph of a $C^2$-function $\varphi$ over the boundary of a strictly convex domain $\mathrm{\Omega }\subset \mathbf{C}\times \mathbf{R}$. Then $\hat{\mathrm{\Gamma }}$ is the graph of a Lipschitz-continuous extension $\mathrm{\Phi }$ of $\varphi$ on $\mathrm{\Omega }$. Moreover, $\hat{\mathrm{\Gamma }}$ is foliated with analytic discs (cf. also Foliation).

The work of Bedford and Klingenberg has been generalized in various directions in [a16], [a21] and [a7]. One ingredient of this theorem is work of Bishop [a5], which gives conditions that guarantee locally the existence of analytic discs with boundary in real submanifolds of sufficiently high dimension. See [a11], [a32] and [a15] for results along this line.

A third situation that is fairly well understood is when $K\subset {\mathbf{C}}^{n+1}$ is a compact set fibred over $T$, that is, $K$ is of the form $K=\{(z,w):z\in T,w\in K_z\}$, where $K_z$ is a compact set in ${\mathbf{C}}^n$ depending on $z$.

In this case the following is true: Let $K\subset {\mathbf{C}}^2$ be a compact fibration over the circle $T$ and suppose that for each $z$ the fibre $K_z$ is connected and simply connected. Then $\hat{K}\mathrm{\setminus }K$ is the union of graphs ${\mathrm{\Gamma }}_f$, where $f\in H^{\mathrm{\infty }}(\mathrm{\Delta })$ and the boundary values $f^{\ast }(z)$ are in $K_z$ for almost all $z\in T$.

Of course, it is possible that $\hat{K}\mathrm{\setminus }K$ is empty. The present theorem is due to Z. Slodkowski, [a22], earlier results are in [a2] and [a10]. Slodkowski proved a similar theorem in ${\mathbf{C}}^{n+1}$ under the assumption that the fibres are convex, see [a23].

Despite these positive results, in general 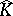$\hat{K}\mathrm{\setminus }K$ need not have analytic structure. This has become clear from examples by Stolzenberg [a25] and Wermer [a31]. Presently (2000) it is not known whether has analytic structure everywhere if 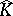$K$ is a (real) submanifold of ${\mathbf{C}}^n$, nor is it known under what conditions is obtained by glueing discs to $K$.

However, it has been shown that in a weaker sense there is always a kind of analytic structure in polynomial hulls. Let $d\theta$ denote Lebesgue measure on the circle $T$ and let $f^{\ast }d\theta$ denote the push-forward of $d\theta$ under a continuous mapping $f:T\to {\mathbf{C}}^n$. Let also $K$ be a compact set in ${\mathbf{C}}^n$. The following are equivalent:

1) $z\in \hat{K}$ and ${\mu }_z$ is a Jensen measure for $z$ supported on $K$;

2) There exists a sequence of analytic discs $f_j:\mathrm{\Delta }\to {\mathbf{C}}^n$ such that $f_j(0)\to z$ and $f_j^{\ast }d\theta /2\pi \to {\mu }_z$ in the weak-$\ast$ sense (cf. also Weak topology).

This was proved in [a6]; [a8] and [a20] contain more information about additional nice properties that can be required from the sequence of analytic discs. Under suitable regularity conditions on $K$, it is shown in [a19] that consists of analytic discs $f$ such that $f^{-1}(K)\cap T$ has Lebesgue measure arbitrary close to $2\pi$.

Another problem is to describe $P(K)$ assuming that $K=\hat{K}$ and given reasonable additional conditions on $K$. In particular, when can one conclude that $P(K)=C(K)$? Recall that a real submanifold $M$ of ${\mathbf{C}}^n$ is totally real at $p\in M$ if the tangent space in $p$ does not contain a complex line (cf. also CR-submanifold). The Hörmander–Wermer theorem is as follows, cf. [a14]: Let $M$ be a sufficiently smooth real submanifold of ${\mathbf{C}}^n$ and let $K_0$ be the subset of $M$ consisting of points that are not totally real. If $K\subset M$ is a compact polynomially convex set that contains an $M$-neighbourhood of $K_0$, then $P(K)$ contains all continuous functions on $K$ that are on $K_0$ the uniform limit of functions holomorphic in a neighbourhood of $K_0$.

See [a17] for a variation on this theme. One can deal with some situations where the manifold is replaced by a union of manifolds; e.g., B.M. Weinstock [a28] gives necessary and sufficient conditions for any compact subset of the union of two totally real $n$-dimensional subspaces of ${\mathbf{C}}^n$ to be polynomially convex; then also $P(K)=C(K)$. See also [a18].

References[edit]