Roses (curves)
 From Encyclopedia of Mathematics - Reading time: 1 min
From Encyclopedia of Mathematics - Reading time: 1 min
Planar curves whose equations in polar coordinates have the form
$$\rho=a\sin k\phi,$$
where $a$ and $k$ are constants. If $k=m/n$ is a rational number, then a rose is an algebraic curve of even order.
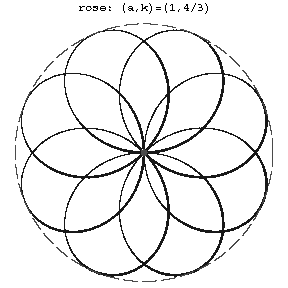
Figure: r082610a
The order of a rose is equal to $m+n$ if $m$ and $n$ are odd, and to $2(m+n)$ if either $m$ or $n$ is even. The entire curve is situated inside the circle of radius $a$ and consists of congruent parts, called petals (see Fig.). If $k$ is an integer, then the rose consists of $k$ petals for $k$ odd and of $2k$ petals for $k$ even. If $k=m/n$ and $m,n$ are relatively prime, then the rose consists of $m$ petals for $m$ and $n$ odd, and of $2m$ petals when either $m$ or $n$ is even.
When $k$ is irrational there are infinitely many petals. Roses belong to the family of cycloidal curves (cf. Cycloidal curve). They are hypocycloids if $k>1$, and epicycloids if $k<1$.
Roses are also related to the family of cycloidal curves by the fact that they are pedals of epi- and hypocycloids with respect to the centre of their fixed circle.
The arc length of a rose is given by an elliptic integral of the second kind. The area of one petal is $S=\pi a^2/4k$.
Roses are also called curves of Guido Grandi, who was the first to describe them in 1728.
References[edit]
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments[edit]
These curves are also called rhodoneas, cf. [a1].
References[edit]
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
| [a2] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
 KSF
KSF