Solvable flow

A flow on a solv manifold $M=G/H$ determined by the action on $M$ of some one-parameter subgroup $g_t$ of the solvable Lie group $G$: If $M$ consists of the cosets $gH$, then under the action of the solvable flow such a coset goes to the coset $g_{t}gH$ at time $t$. A particular case of a solvable flow is a nil-flow; in the general case the properties of a solvable flow can be considerably more diverse.

References[edit]

[1]	L. Auslander, L. Green, F. Hahn, "Flows on homogeneous spaces" , Princeton Univ. Press (1963)
[2]	A.M. Stepin, "Flows on solvmanifolds" Uspekhi Mat. Nauk , 24 : 5 (1969) pp. 241 (In Russian)
[3]	L. Auslander, "An exposition of the structure of solvmanifolds. Part II: 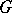-induced flows" Bull. Amer. Math. Soc. , 79 : 2 (1973) pp. 262–285
[4]	A.V. Safonov, "Spectral type of 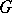-induced ergodic flows" Functional Anal. Appl. , 14 : 4 (1980) pp. 315–317 Funkts. Anal. i Prilozhen. , 14 : 4 (1980) pp. 81–82
[5]	L. Auslander, L. Green, "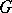-induced flows and solvmanifolds" Amer. J. Math. , 88 (1966) pp. 43–60

Comments[edit]

In many cases dynamical properties of the flow, such as ergodicity, can be deduced from algebraic properties of $G$ and $H$. The Kronecker theorem implies ergodicity for the case $G={\mathbf{R}}^n$, $H={\mathbf{Z}}^n$, the integer lattice, and the flow (written additively) given by $g_t(x+{\mathbf{Z}}^n)=x+ta+{\mathbf{Z}}^n$, where $x+{\mathbf{Z}}^n$ is a coset of ${\mathbf{R}}^n/{\mathbf{Z}}^n$ and $a\in {\mathbf{R}}^n$ is a fixed vector whose components are linearly independent over the rational numbers. When $G=\mathrm{SL}(2,\mathbf{R})$ and $H$ is a discrete subgroup, certain one-parameter subgroups of $G$ correspond to geodesic and horocycle flow (cf. Geodesic flow; Horocycle flow) on unit tangent bundles of surfaces of constant negative curvature (cf. Constant curvature, space of).

References[edit]