Whitham equations
 From Encyclopedia of Mathematics - Reading time: 15 min
From Encyclopedia of Mathematics - Reading time: 15 min
Perhaps the proper beginning of Whitham theory is Whitham's work [a75], [a74], which can be viewed as a crucible of various averaging ideas subsequently developed in e.g. [a3], [a4], [a12], [a13], [a14], [a27], [a28], [a29], [a42], [a49], [a50], [a61], [a73] to theories involving multi-phase averaging, Hamiltonian systems and weakly deformed soliton lattices. The term "Whitham equations" then became associated with the moduli dynamics of Riemann surfaces and this fits naturally into work on topological field theories, Frobenius manifolds, renormalization groups, coupling constants, and Seiberg–Witten theory (cf. also Seiberg–Witten equations), along with singularity theory, isomonodromy deformations, quantum cohomology and $K$-theory, Gromov–Witten invariants, Witten–Dijkgraaf–Verlinde–Verlinde equations, etc. (see the references below or the survey material in [a5], [a6], [a7], [a8], [a9], [a10]).
Averaging.[edit]
One of the most important applications of averaging theory and the Whitham equation is to the Korteweg–de Vries equation
\begin{equation} \tag{a1} u _ { t } - 6 u u _ { x } + u _ { xxx } = 0. \end{equation}
Key early papers on averaging for this equation include [a27] and [a49]. The basic ideas of G. Whitham are discussed in [a74], [a75]. Other important papers include [a1], [a2], [a25], [a65].
The key idea is averaging out fast scales; one introduces two scales: the "fast" scale $( x , t )$ and "slow" scale ($X = \epsilon x$, $T = \epsilon t$),  small. One obtains a class of ( "finite-gap" ) solutions of the form
small. One obtains a class of ( "finite-gap" ) solutions of the form
\begin{equation} \tag{a2} u ( x , t ) = U = f _ { g } ( \theta _ { 1 } , \ldots , \theta _ { g } ), \end{equation}
where $f _ { g }$ is a meromorphic function of $g$ variables and $\theta _ { i } = \kappa _ { i } + \omega _ { i } + \widehat { \theta } _ { i }$, where the parameters $U$, $\kappa_i$, $\omega _ { i }$ depend only on the slow variables.
One can then write down the evolution equations for $g$-phase wave trains in terms of differentials on an associated Riemann surface.
The Whitham equation for the Korteweg–de Vries equation is given by
\begin{equation} \tag{a3} \frac { \partial d \omega _ { 1 } } { \partial T } = \frac { \partial d \omega _ { 3 } } { \partial X }, \end{equation}
where 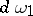 and
and 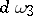 are Abelian differentials on the Riemann surface of genus $g$ given by $y ^ { 2 } = R _ { g } ( \lambda )$ (cf. also Differential on a Riemann surface; Abelian differential; Riemann surface), where
are Abelian differentials on the Riemann surface of genus $g$ given by $y ^ { 2 } = R _ { g } ( \lambda )$ (cf. also Differential on a Riemann surface; Abelian differential; Riemann surface), where
\begin{equation*} R _ { g } ( \lambda ) = \prod _ { i = 0 } ^ { 2 g } ( \lambda - \lambda _ { i } ) \end{equation*}
and the branch points $\lambda _ { i }$ are real and are assumed to satisfy $\lambda _ { 0 } < \ldots < \lambda _ { 2 g }$.
Explicitly,
\begin{equation} \tag{a4} d \omega _ { 1 } ( \lambda ) = \frac { \prod _ { i = 1 } ^ { g } ( \lambda - \alpha _ { i } ) } { \sqrt { R _ { g } ( \lambda ) } } d \lambda \sim \end{equation}
\begin{equation*} \sim \frac { d \lambda } { \sqrt { \lambda } } + ( \text { holomorphic } ) , \text { as } \lambda \rightarrow \infty , \end{equation*}
\begin{equation} \tag{a5} d \omega _ { 3 } ( \lambda ) = \frac { \lambda ^ { g + 1 } - \frac { 1 } { 2 } \sigma _ { 1 } \lambda ^ { g } + \beta _ { 1 } \lambda ^ { g - 1 } + \ldots + \beta _ { g } } { \sqrt { R _ { g } ( \lambda ) } } d \lambda \sim \end{equation}
\begin{equation*} \sim \sqrt { \lambda } d \lambda + \text { (holomorphic), as } \lambda \rightarrow \infty. \end{equation*}
Here, the coefficients $\{ \alpha _ { j } , \beta _ { j } \}$ are determined by
\begin{equation*} \oint _ { A _ { j } } d \omega _ { 1 } = \oint _ { A _ { j } } d \omega _ { 3 } = 0 , j = 1 , \dots , g , \end{equation*}
the vanishing of the contour integral along the canonical $A _ { j }$-cycle, and $\sigma _ { 1 } = \sum _ { i = 0 } ^ { 2 g } \lambda _ { i }$.
Then the averaged solution of the Korteweg–de Vries equation is given by
\begin{equation*} \overline { u } ( x , t ) = \frac { 1 } { 2 } \sum _ { i = 0 } ^ { 2 g } \lambda _ { i } - \sum _ { j = 0 } ^ { g } \alpha _ { j }. \end{equation*}
Note that when $g = 0$, the equation reduces to the dispersionless Korteweg–de Vries equation (Hopf–Burgers equation) with $\lambda _ { 0 } = 2 \overline { u }$ and $\lambda _ { 1 } = \ldots = \lambda _ { 2 g } = \alpha _ { 1 } = \ldots = \alpha _ { g } = 0$, i.e.,
\begin{equation*} \frac { \partial \overline { u } } { \partial T } = \overline { u } \frac { \partial \overline { u } } { \partial X }. \end{equation*}
The Whitham equation for the discrete Toda lattice (cf. Toda lattices) is treated in [a4] where shock formation is analyzed. Shocks for the Korteweg–de Vries equation are analyzed in [a34], [a35].
The discrete Ablowitz–Ladik equations are analyzed in [a60].
The Whitham equations are also important in the analysis of the non-linear Schrödinger equation (cf. also Benjamin–Feir instability) and non-linear optics, see for example [a36], [a48], [a64] and references therein.
General Whitham theory.[edit]
More generally, for any compact Riemann surface $\Sigma _ { g }$ of genus $g$ and point $Q \sim \infty$, the Baker–Akhiezer function $\psi$ gives rise to a KP-hierarchy (cf. also KP-equation). In particular, following [a11], [a27], [a42], $\psi$ can be written as
\begin{equation} \tag{a6} \psi ( P ) = \operatorname { exp } \left( \sum t _ { n } \Omega _ { n } \right) \phi \left( \sum t _ { n } \overset{\rightharpoonup}{ V } _ { n } , P \right) , \end{equation}
where $d \Omega _ { n } \sim d ( \lambda ^ { n } ) + \ldots$ near $\infty$ and $\int _ { A _ { i } } d \Omega _ { n } = 0$ with $\int _ { B _ { i } } d \Omega _ { n } = V _ { i n } \sim ( \overset{\rightharpoonup}{ V _ { n } } ) _ { i }$. Here, $\phi$ is periodic and $\Omega _ { n } = \Omega _ { n } ( T _ { m } )$ with $\overset{\rightharpoonup} { V } _ { n } = \overset{\rightharpoonup} { V } _ { n } ( T _ { m } )$ for slow times $T _ { m }$ defined via $T _ { m } = \epsilon t _ { m }$ and $\overset{\rightharpoonup} { \theta } = \sum t _ { n } \overset{\rightharpoonup} { V } _ { n }$ is a point in the Jacobian $\operatorname { Jac } ( \Sigma _ { g } )$ (cf. also Jacobi variety). Assuming, for simplicity, that the periods are incommensurable, by ergodicity one finds
\begin{equation*} \frac { 1 } { 2 L } \int _ { - L } ^ { L } \phi d t _ { i } = \langle \phi \rangle = \left( \frac { 1 } { 2 \pi } \right) ^ { 2 g } \int \ldots \int \phi d ^ { 2 g } \theta . \end{equation*}
With $\psi ^ { * }$ corresponding to the adjoint Baker–Akhiezer function, one can think now of multi-scale analysis of $\psi \psi ^ { * } d \widetilde { \Omega }$ with $\partial _ { i } \rightarrow \partial _ { i } + \epsilon ( \partial / \partial T _ { i } )$ plus averaging over the fast times (here, $d \tilde { \Omega } = d \lambda + O ( \lambda ^ { - 2 } ) d \lambda$ near $\infty$ is canonically specified). This corresponds to looking at an  expansion and setting the average first-order term to zero, leading to the Whitham equations
expansion and setting the average first-order term to zero, leading to the Whitham equations
\begin{equation} \tag{a7} \frac { \Omega _ { n } } { \partial T _ { m } } = \frac { \partial \Omega _ { m } } { \partial T _ { n } }. \end{equation}
Seiberg–Witten theory.[edit]
Given a low-energy effective action for an $N = 2$ susy gauge theory with partition function
\begin{equation} \tag{a8} Z ( t , \phi ) = \int _ { \phi _ { 0 } } \mathcal{D} \phi \operatorname { exp } [ S ( t , \phi ) ], \end{equation}
with 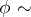 fields, $t \sim $ coupling constants and
fields, $t \sim $ coupling constants and 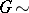 gauge group in the background, it turns out (e.g. in matrix models) that $Z ( t , \phi )$ will often be a tau-function of KP–Toda type via Ward identities and Virasoro (origin of integrability). Recall that tau-functions are basic ingredients in integrable system theory (cf. also KP-equation; Toda lattices) and e.g.
gauge group in the background, it turns out (e.g. in matrix models) that $Z ( t , \phi )$ will often be a tau-function of KP–Toda type via Ward identities and Virasoro (origin of integrability). Recall that tau-functions are basic ingredients in integrable system theory (cf. also KP-equation; Toda lattices) and e.g.
\begin{equation} \tag{a9} \psi = \frac { \operatorname { exp } \left( \sum t _ { n } \lambda ^ { n } \right) \tau ( t_{ j} - ( 1 / j \lambda ^ { j } ) ) } { \tau ( t _ { j } ) }. \end{equation}
For $Z \sim \tau$ one has an effective (classical-type) dynamics in the $t$ variables and averaging corresponds in some sense to suppressing fast oscillations (which suggests a renormalization procedure); alternatively, it is also in some sense related to a quantization procedure in the first WKBJ approximation, which produces slow dynamics on the action variables (Hamiltonians $\sim$ Casimirs from $\widetilde{ g } = \text { Lie } ( G )$; cf. also Casimir element; Kac–Moody algebra), which is equivalent in many situations to dynamics on the moduli of the underlying spectral curves. Thus, the quantum arena shifts to the quantum moduli space and the $T _ { n }$ appear as renormalized coupling constants in one approach and as deformation parameters of moduli in another. The tau-function $\tau$ goes to a quasi-classical tau-function whose logarithm (after  adjustment) is called the pre-potential $F$ and this serves as a generating function for correlators and as a vehicle for expressing further renormalization effects. Consider (cf. [a31], [a32], [a33], [a37], [a38], [a39], [a40], [a41], [a62]) the following example of Seiberg–Witten Toda curves for $\mathcal{N} = 2$ susy Yang–Mills with $G = \operatorname {SU} ( N )$, $N = N _ { c }$, no masses and moduli $u _ { k } \in \mathcal{M} =$ quantum moduli space of inequivalent vacua:
adjustment) is called the pre-potential $F$ and this serves as a generating function for correlators and as a vehicle for expressing further renormalization effects. Consider (cf. [a31], [a32], [a33], [a37], [a38], [a39], [a40], [a41], [a62]) the following example of Seiberg–Witten Toda curves for $\mathcal{N} = 2$ susy Yang–Mills with $G = \operatorname {SU} ( N )$, $N = N _ { c }$, no masses and moduli $u _ { k } \in \mathcal{M} =$ quantum moduli space of inequivalent vacua:
\begin{equation} \tag{a10} y ^ { 2 } = P ^ { 2 } - 4 \Lambda ^ { 2 N }, \end{equation}
\begin{equation*} y = \Lambda ^ { N } \left( w - \frac { 1 } { w } \right) , P = \lambda ^ { N } - \sum _ { 2 } ^ { N } u _ { k } \lambda ^ { N - k } = \Lambda ^ { N } \left( w + \frac { 1 } { w } \right) . \end{equation*}
Here, $\lambda$ is the quantum scale, $\xi $ is a local coordinate at $\infty_{\pm}$ with $\Lambda \xi \sim w ^ {\mp ( 1 / N ) }$ with $w \rightarrow \infty$ at $\infty _+$ and $w \rightarrow 0$ at $\infty _-$, and $g = N - 1$. One defines
\begin{equation} \tag{a11} d \hat { \Omega } _ { n } = P _ { + } ^ { n / N } \left( \frac { d w } { w } \right) \end{equation}
and
\begin{equation*} d \Omega _ { n } = d \hat { \Omega } _ { n } - \sum _ { 1 } g \left( \oint _ { A _ { j } } d \hat { \Omega} _ { n } \right) d \omega _ { j } \end{equation*}
($n < 2 N$ for technical reasons and $d \omega_{j} \sim$ holomorphic differentials). The standard Whitham theory is now based on
\begin{equation} \tag{a12} d S = \sum _ { 1 } ^ { M } T _ { n } d \widehat { \Omega } _ { n } = \sum _ { 1 } ^ { M } T _ { n } d \Omega _ { n } + \sum _ { 1 } ^ { g } \alpha _ { j } d \omega _ { j }, \end{equation}
where $M < 2 N$ and $T _ { 0 } = 0$ for $N _ { f } = 0$. One has then Whitham equations
\begin{equation} \tag{a13} \frac { \partial d \Omega _ { A } } { \partial T _ { B } } = \frac { \partial d \Omega _ { B } } { \partial T _ { A } } \end{equation}
with $\partial d S / \partial \alpha_j = d \omega_j$ and $\partial d S / \partial T _ { n } = d \omega _ { n }$ for $( T _ { n } , \alpha _ { j } )$ independent. The pre-potential $F$ arises via
\begin{equation} \tag{a14} \frac { \partial F } { \partial \alpha _ { j } } = \oint _ { B _ { j } } d S \end{equation}
and $\partial _ { n } F = ( 1 / 2 \pi i n ) \operatorname { Res } _ { 0 } \xi ^ { - n } d S$, where 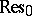 involves $\infty_{\pm}$ and the Seiberg–Witten differential is
involves $\infty_{\pm}$ and the Seiberg–Witten differential is
\begin{equation} \tag{a15} d S _ { S W } = d \widehat { \Omega } _ { 1 } = \lambda \left( \frac { d w } { w } \right) = \lambda \frac { d P } { y } = \lambda \frac { d y } { P }. \end{equation}
Thus, for $T _ { n } = \delta _ { n , 1 }$ one has the Seiberg–Witten situation $F ^ { \text{SW} } = \widetilde { F }$ and one writes then also $a _ { i } = \alpha _ { i }$.
General framework.[edit]
The Whitham formulation of I. Krichever, developed in great detail with D.H. Phong (cf. [a43], [a44], [a45], [a46], [a47]), involves a Riemann surface $\Sigma _ { g }$ with $M$ punctures $P _ { \alpha }$. One picks in an ad hoc manner two Abelian differentials $d E$ and $d Q$ having certain properties and sets $d S = Q d E$ as a Seiberg–Witten-type differential. Moduli space parameters are constructed and suitable submanifolds of a symplectic nature are parametrized by Whitham times $T _ { A }$ with corresponding differentials $d \Omega _ { A }$. For suitable choices of $d E$ and $d Q$ the formulation is adequate for Seiberg–Witten-type situations and topological field theories with Witten–Dijkgraaf–Verlinde–Verlinde equations will arise as well.
Soft susy breaking.[edit]
There is another role for Whitham times, via (cf. [a26], [a55])
\begin{equation} \tag{a16} \hat{T} _ { n } = T _ { n } T _ { 1 } ^ { - 1 } , \hat { u } _ { k } = T _ { 1 } ^ { k } u _ { k }, \end{equation}
and $\hat { a } _ { i } = \alpha _ { i } ( u _ { k } , T _ { 1 } , \hat{T} _ { n > 1 } = 0 ) = T _ { 1 } a _ { i } ( u _ { k } , \Lambda = 1 ) = a _ { i } ( \hat { u } _ { k } , \Lambda = T _ { 1 } )$ (note $T _ { 1 } \sim \Lambda$ in the Seiberg–Witten situation). Then one defines
\begin{equation} \tag{a17} s _ { 1 } = - i \operatorname { log } ( \lambda ) \end{equation}
and $s _ { n } = - i \hat{T} _ { n }$ and these are promoted to spurion superfields $\mathcal{S} _ { n } = s _ { n } + \theta ^ { 2 } F _ { n }$ and $V _ { n } = ( 1 / 2 ) D _ { n } \theta ^ { 2 } \overline { \theta } ^ { 2 }$ in $\mathcal{N} = 1$ superfield language ($\theta$ and $\overline{\theta}$ are Grassmann variables while $D _ { n }$ and $F _ { n }$ are auxiliary fields). One has a family of non-susy theories and soft susy breaking $\mathcal{N} = 2 \rightarrow \mathcal{N} = 0$ is achieved by fixing $s _ { n } = 0$ for $n > 1$ and using $D _ { n }$, $F _ { n }$ ($n \geq 1$) as susy breaking parameters (actually, the $F _ { n }$ alone will suffice). In any event, one can develop formulas involving $\lambda$, $\tilde{T} _ { n }$ and $\alpha_j$ derivatives of the pre-potential and eventually parametrize soft susy breaking terms induced by all of the Casimirs.
Isomonodromy.[edit]
Various isomonodromy problems can be treated by multi-scale analysis to produce results indicating that isomonodromy deformations in WKB approximation correspond to modulation of isospectral problems (with Whitham-type equations as modulation equations). One can generate a pre-potential, period integrals, etc. as in Seiberg–Witten theory (see e.g. [a66], [a67], [a68], [a69], [a70]). There are also isomonodromy connections to the Knizhnik–Zamolodchikov–Bernard equations (cf. [a51], [a52], [a53], [a63]); these equations arise in various ways in conformal field theory, geometric quantization of flat bundles, etc. Here one takes $F B ( \Sigma _ { g } , G )$ as flat vector bundles over $\Sigma _ { g }$ with $G = \operatorname{GL} ( N ,\bf C )$ and smooth connections $\mathcal{A} \sim ( A , \overline { A } )$. "Flat" means zero curvature and with an arbitrary $\kappa$ this has the form
\begin{equation} \tag{a18} ( \kappa \partial + A ) \psi = 0 \end{equation}
and $( \overline { \partial } + \overline { A } ) \psi = 0$. Let $\mu \in \Omega ^ { - 1,1 } ( \Sigma _ { g } )$ (Beltrami differentials), so $\mu = \mu ( z , \bar{z} ) \partial _ { \bar{z} } \otimes d \bar{z}$ and set 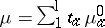 , where $\text{l} = 3 g - 3$ ($g > 1$) and $\mu _ { a } ^ { 0 }$ is a basis in $T \mathcal{M} _ { g }$. Then (a18) becomes
, where $\text{l} = 3 g - 3$ ($g > 1$) and $\mu _ { a } ^ { 0 }$ is a basis in $T \mathcal{M} _ { g }$. Then (a18) becomes
\begin{equation} \tag{a19} ( \kappa \partial + A ) \psi = 0 \end{equation}
and $( \overline { \partial } + \mu \partial + \overline { A } ) \psi = 0$. Let $\gamma$ be a homotopically non-trivial cycle in $\Sigma _ { g }$ such that $( z_0 , \overline{z}_0 ) \in \gamma$ with $\psi ( z _ { 0 } , \overline{z} _ { 0 } ) = I$ and write $\mathcal{Y} ( \gamma ) = \psi ( z _ { 0 } , \overline{z} _ { 0 } ) | _ { \gamma } = P \operatorname { exp } ( \oint _ { \gamma } \mathcal{A} )$ (path-ordered exponential), which yields a representation of $\Pi _ { 1 } ( \Sigma _ { g } , z _ { 0 } )$ in $\operatorname {GL} ( N , \mathbf{C} )$. The independence of monodromy $\mathcal{Y}$ to complex structure deformation corresponds to 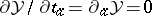 for $a = 1 , \dots , \text{l}$. Compatibility with (a19) requires
for $a = 1 , \dots , \text{l}$. Compatibility with (a19) requires
\begin{equation} \tag{a20} \partial _ { a } A = 0 \text { and } \partial \overline { A } = ( 1 / \kappa ) A \mu _ { a } ^ { 0 }. \end{equation}
These equations are Hamiltonian when $F B ( \sigma _ { g } , G )$ has a symplectic form $\omega ^ { 0 } = \int \Sigma _ { g } \langle \delta A , \delta \overline { A } \rangle$ with Hamiltonians 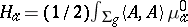 . Consider the bundle $\mathcal{P}$ over $\mathcal{M} _ { g }$ with fibre $F B$ (using $( A , \overline { A } , t \sim t _ { a } )$ as local coordinates). A gauge fixing plus flatness corresponds to reduction from $F B \rightarrow \widetilde { F B }$ and one can (via WZW theory) fix the gauge to get a bundle $\tilde {\cal P }$ with fibre $\widetilde { F B }$ and equations
. Consider the bundle $\mathcal{P}$ over $\mathcal{M} _ { g }$ with fibre $F B$ (using $( A , \overline { A } , t \sim t _ { a } )$ as local coordinates). A gauge fixing plus flatness corresponds to reduction from $F B \rightarrow \widetilde { F B }$ and one can (via WZW theory) fix the gauge to get a bundle $\tilde {\cal P }$ with fibre $\widetilde { F B }$ and equations
\begin{equation} \tag{a21} ( \kappa \partial + L ) \psi = 0 \end{equation}
with $( \overline { \partial } + \mu \partial + \overline{L}) \psi = 0$ and $( \kappa \partial _ { a} + M _ { a } ) \psi = 0$, where $M _ { a }$ comes from the gauge transformation. Putting in the canonical form via local coordinates $( v _ { i } , u _ { i } )$ in $\widetilde { F B }$, where $i = 1 , \dots , M = ( N ^ { 2 } - 1 ) ( g - 1 )$, one can write
\begin{equation} \tag{a22} \omega ^ { 0 } = ( \delta v , \delta u ) \end{equation}
with $\omega = \omega ^ { 0 } - ( 1 / \kappa ) \sum \delta H _ { \alpha } \delta t _ { \alpha }$. Using the Poincaré–Cartan invariant form $\Theta = ( u , \delta v ) - ( 1 / \kappa ) \sum H _ { a } \delta t _ { a }$ there exist $3 g - 3$ vector fields  which annihilate $\Theta$. With $\{ .\}_0 \sim \omega ^ { 0 }$-structure this gives
which annihilate $\Theta$. With $\{ .\}_0 \sim \omega ^ { 0 }$-structure this gives
\begin{equation} \tag{a23} \kappa \partial _ { s } H _ { r } - \kappa \partial _ { r } H _ { s } + \{ H _ { s } , H _ { r } \} _ { 0 } = 0. \end{equation}
These equations define flat connections in $\tilde {\cal P }$ and are referred to as a Whitham hierarchy of isomonodromic deformations. For a given $f ( u , v , t )$ on $\tilde {\cal P }$ they take the form
\begin{equation} \tag{a24} \frac { d f } { d t _ { s } } = \kappa \partial _ { s } f + \{ H _ { s } , f \} \end{equation}
and one can introduce a pre-potential $F$ on $\tilde {\cal P }$ giving Hamilton–Jacobi equations (cf. Hamilton–Jacobi theory)
\begin{equation} \tag{a25} \kappa \partial _ { s } F + H _ { s } \left( \frac { \delta F } { \delta u } , u , t \right) = 0. \end{equation}
Thus, one has a derivation of deformation equations, properly referred to as a Whitham hierarchy, which involves no averaging or multi-scale analysis. One can also compare the Baker–Akhiezer function $\psi$ in the Whitham hierarchy of isomonodromic deformations with elements of a certain Hitchin hierarchy (cf. also Hitchin system) using a WKB approximation with fast times $t _ { S } ^ { H }$ and slow times $T _ { S } \sim t _ { s }$.
Contact terms.[edit]
For $\mathcal{N} = 2$ susy gauge theory on a $4$-manifold with $b _ { 2 + } = 1$ there is a $u$-plane integral for, say, $\operatorname{SU} ( N )$ situations, which can be related to a Toda theory with fast and slow (Whitham) times (cf. [a55], [a56], [a57], [a58], [a59], [a71], [a72]).
Witten–Dijkgraaf–Verlinde–Verlinde.[edit]
There is a beautiful and elaborate theory of B. Dubrovin and others based on Frobenius manifolds (cf. [a15], [a16], [a17], [a18], [a19], [a20], [a21], [a22], [a23], [a24]). This approach is especially pleasing since there is a great deal of motivation and natural structure. There are many connections to mathematics and physics and this approach has led to extensive development in Frobenius manifolds, quantum cohomology and $K$-theory, singularity theory, Witten–Dijkgraaf–Verlinde–Verlinde, etc. (see e.g. [a15], [a16], [a17], [a18], [a19], [a20], [a21], [a30], [a54]). A simple Hurwitz-space Korteweg–de Vries–Landau–Ginsburg model is as follows.
Let ${\cal M} _ { g , n + 1}$ be the moduli space of $g$ gap Korteweg–de Vries solutions based on $L = \partial ^ { n + 1 } - q _ { 1 } \partial ^ { n - 1 } - \ldots - q _ { n }$ with ramification based on $W = p ^ { n + 1 } - q _ { 1 } p ^ { n - 1 } - \ldots - q _ { n }$. One defines Whitham times
\begin{equation} \tag{a26} T _ { i } = - \frac { n + 1 } { n + 1 - i } \operatorname { Res } _ { \infty } W ^ { 1 - [ i / ( n + 1 ) ] } d p, \end{equation}
\begin{equation*} T _ { n + \alpha } = \frac { 1 } { 2 \pi i } \oint _ { A _ { \alpha } } p d W , T _ { g + n + \alpha } = \oint _ { B _ { \alpha } } d p, \end{equation*}
where $1 \leq i \leq n$ and $1 \leq \alpha \leq g$. These are flat times for a certain metric and determine a Whitham hierarchy, a Frobenius manifold and a topological field theory of Landau–Ginsburg type satisfying the Witten–Dijkgraaf–Verlinde–Verlinde equations (associativity equations for related field correlators).
References[edit]
| [a1] | V.V. Avilov, S.P. Novikov, "Evolution of the Whitham zone in KdV theory" Soviet Phys. Dokl. , 32 (1987) pp. 366–368 MR0895679 |
| [a2] | V.V. Avilov, I.M. Krichever, S.P. Novikov, "Evolution of a Whitham zone in the Korteweg–de Vries theory" Soviet Phys. Dokl. , 32 (1987) pp. 564–566 MR902689 Zbl 0655.65132 |
| [a3] | M. Ablowitz, D. Benney, "The evolution of multi-phase modes of nonlinear dispersive waves" Stud. Appl. Math. , 49 (1970) pp. 225–238 Zbl 0203.41001 |
| [a4] | A. Bloch, Y. Kodama, "Dispersive regularization of the Whitham equation for the Toda lattice" SIAM J. Appl. Math. , 52 (1992) pp. 909–928 MR1174037 Zbl 0757.34014 |
| [a5] | "Integrability: The Seiberg–Witten and Whitham equations" H. Braden (ed.) I. Krichever (ed.) , Gordon & Breach (2000) MR1816181 Zbl 0948.00012 |
| [a6] | R. Carroll, "Various aspects of Whitham times" math-ph , 9905010 (1999) MR1776704 Zbl 0981.81062 |
| [a7] | R. Carroll, "Various aspects of Whitham times" Acta Applic. Math. , 60 (2000) pp. 225–316 MR1776704 Zbl 0981.81062 |
| [a8] | R. Carroll, "Remarks on Whitham dynamics" Applic. Anal. , 70 (1998) pp. 127–146 MR1671571 Zbl 1015.37500 |
| [a9] | R. Carroll, "Some survey remarks on Whitham theory and EM duality" Nonlin. Anal. , 30 (1997) pp. 187–198 MR1489780 Zbl 0955.35068 |
| [a10] | R. Carroll, "Quantum theory, deformation and integrability" , Elsevier (2000) MR1838460 Zbl 1008.81502 |
| [a11] | R. Carroll, J. Chang, "The Whitham equations revisited" Applic. Anal. , 64 (1997) pp. 343–378 MR1460089 Zbl 0887.14011 |
| [a12] | B. Dubrovin, S. Novikov, "Hydrodynamics of weakly deformed soliton lattices" Russian Math. Surveys , 44 (1989) pp. 35–124 MR1037010 Zbl 0712.58032 |
| [a13] | B. Dubrovin, S. Novikov, "Hydrodynamics of soliton lattices" Math. Phys. Rev. , 9 (1991) pp. 3–136 MR1271587 Zbl 0845.58027 Zbl 0712.58032 |
| [a14] | B. Dubrovin, I. Krichever, S. Novikov, "Topological and algebraic geometry methods in contemporary mathematical physics II" Math. Phys. Rev. , 3 (1982) pp. 1–150 Zbl 0534.58002 |
| [a15] | B. Dubrovin, "Geometry of 2D topological field theories" M. Francaviglia (ed.) et al. (ed.) , Integrable Systems and Quantum Groups , Lecture Notes in Mathematics , 1620 , Springer (1996) pp. 120–348 MR1397274 Zbl 0841.58065 |
| [a16] | B. Dubrovin, "Integrable systems in topological field theory" Nucl. Phys. B , 379 (1992) pp. 627–689 MR1175565 |
| [a17] | B. Dubrovin, "Hamiltonian formalism of Whitham-type hierarchies and topological Landau–Ginsburg models" Commun. Math. Phys. , 145 (1992) pp. 195–207 MR1155289 Zbl 0753.58039 |
| [a18] | B. Dubrovin, "Integrable systems and classification of $2$-dimensional topological field theories" O. Babelon (ed.) et al. (ed.) , Integrable Systems: The Verdier Memorial Conf. , Birkhäuser (1993) pp. 313–359 MR1279829 |
| [a19] | B. Dubrovin, Y. Zhang, "Extended affine Weyl group and Frobenius manifolds" hep-th , 9611200 (1996) MR1606165 |
| [a20] | B. Dubrovin, Y. Zhang, "Bi-Hamiltonian hierarchies in 2D topologigical field theory on one-loop approximation" hep-th , 9712232 (1997) |
| [a21] | B. Dubrovin, Y. Zhang, "Frobenius manifolds and Virasoro constraints" hep-th , 9808048 (1998) MR1740678 Zbl 0963.81066 |
| [a22] | B. Dubrovin, "Painlevé transcendents and two-dimensional topological field theory" Math. AG , 9803107 (1998) MR1713580 |
| [a23] | B. Dubrovin, "Geometry and analytic theory of Frobenius manifolds" Math. AG , 9807034 (1998) MR1648082 Zbl 0916.32018 |
| [a24] | B. Dubrovin, "Flat pencils of metrics and Frobenius manifolds" Math. DG , 9803106 (1998) MR1672100 Zbl 0963.53054 |
| [a25] | B. Dubrovin, "Functionals of the Peierls–Fröhlich type and the variational principle for the Whitham equations" V.M. Buchstaher (ed.) et al. (ed.) , Solitons, Geometry and Topology: On the Crossroad , Amer. Math. Soc. Transl. (2) , 179 (1997) pp. 35–44 Zbl 0902.35101 |
| [a26] | J. Edelstein, M. Mariño, J. Mas, "Whitham hierarchies, instanton corrctions and soft supersymmetry breaking in $N = 2$ $SU( N )$ super Yang–Mills theory" hep-th , 9805172 (1998) |
| [a27] | H. Flaschka, M. Forest, D. McLaughlin, "Multiphase averaging and the inverse spectral solution of KdV" Commun. Pure Appl. Math. , 33 (1979) pp. 739–784 |
| [a28] | H. Flaschka, A. Newell, "Monodromy- and spectrum preserving deformations I" Commun. Math. Phys. , 76 : 190 (1980) pp. 65–116 MR0588248 Zbl 0439.34005 |
| [a29] | H. Flaschka, A. Newell, "Multiphase similarity solutions of integrable evolution equations" Physica 3D (1981) pp. 203–221 MR0577102 Zbl 1194.37102 |
| [a30] | A. Givental, "On the WDVV-equation in quantum K-theory" Math. AG , 0003158 (2000) MR1786492 Zbl 1081.14523 |
| [a31] | A. Gorsky, I. Krichever, A Marshakov, A. Mironov, A. Morozov, "$N = 2$ supersymmetric QCD and integrable spin chains: Rotational case $N _ { f } < 2 N _ { c }$" Phys. Lett. B , 355 (1996) pp. 466–474 |
| [a32] | A. Gorsky, A. Marshakov, A. Mironov, A. Morozov, "RG equations from Whitham hierarchy" hep-th , 9802007 (1998) MR1640033 Zbl 0951.37022 |
| [a33] | A. Gorsky, A. Marshakov, A. Mironov, A. Morozov, "RG equations from Whitham hierarchy" Nucl. Phys. B , 527 (1998) pp. 690–716 MR1640033 Zbl 0951.37022 |
| [a34] | A.V. Gurevich, L.P. Pitaevskii, JETP Letters , 17 (1974) pp. 193–195 |
| [a35] | A.V. Gurevich, L.P. Pitaevskii, Soviet Phys. JETP , 38 (1974) pp. 291–297 |
| [a36] | A. Hasegawa, Y. Kodama, "Solitons in optical communications" , Oxford Univ. Press (1999) Zbl 0834.35125 Zbl 0840.35092 |
| [a37] | H. Itoyama, A. Morozov, "Integrability and Seiberg–Witten theory: Curves and periods" hep-th , 9511126 (1995) MR1413477 Zbl 0925.81362 |
| [a38] | H. Itoyama, A. Morozov, "Prepotential and Seiberg–Witten theory" hep-th , 9512161 (1995) MR1969691 MR1449320 Zbl 0982.32019 |
| [a39] | H. Itoyama, A. Morozov, "Integrability and Seiberg–Witten theory" hep-th , 9601168 (1996) MR1449902 MR1413477 Zbl 0925.81362 |
| [a40] | H. Itoyama, A. Morozov, "Integrability and Seiberg–Witten theory—curves and periods" Nucl. Phys. B , 477 (1996) pp. 855–877 MR1413477 Zbl 0925.81362 |
| [a41] | H. Itoyama, A. Morozov, "Prepotential and Seiberg–Witten theory" Nucl. Phys. B , 491 (1997) pp. 529–573 MR1449320 Zbl 0982.32019 |
| [a42] | I. Krichever, "The averaging method for the two-dimensional integrable equations" Funct. Anal. Appl. , 22 (1988) pp. 200–213 MR961760 |
| [a43] | I. Krichever, "The $\tau$-function of the universal Whitham hierarchy, matrix models and topological field theories" Commun. Pure Appl. Math. , 47 (1994) pp. 437–475 MR1272384 |
| [a44] | I. Krichever, "Algebraic-geometrical methods in the theory of integrable equations and their perturbations" Acta Applic. Math. , 39 (1995) pp. 93–125 MR1329557 Zbl 0840.35095 |
| [a45] | I. Krichever, "The dispersionless Lax equations and topological minimal methods" Commun. Math. Phys. , 143 (1992) pp. 415–429 |
| [a46] | I. Krichever, D. Phong, "Symplectic forms in the theory of solitons" hep-th , 9708170 (1998) MR1726930 Zbl 0931.35148 |
| [a47] | I. Krichever, D. Phong, "On the integral geometry of soliton equations and $N = 2$ supersymetric gauge theories" J. Diff. Geom. , 45 (1997) pp. 349–389 |
| [a48] | Y. Kodama, "The Whitham equations for optical communication: Mathematical theory of NRZ" SIAM J. Appl. Math. , 59 : 66 (1999) pp. 2162–2192 MR1726195 |
| [a49] | P. Lax, D. Levermore, "The small dispersion limit of the Korteweg–de Vries equation I—III" Commun. Pure Appl. Math. , 36 (1983) pp. 253–290; 571–593; 809–829 |
| [a50] | D. Levermore, "The hyperbolic nature of the zero dispersion KdV limit" Commun. Partial Diff. Eqs. , 13 (1988) pp. 495–514 MR0920912 Zbl 0678.35081 |
| [a51] | A. Levin, M. Olshanetsky, "Painleé–Calogero correspondence" alg-geom , 9706010 (1997) |
| [a52] | A. Levin, M. Olshanetsky, "Classical limit of the Kniznik–Zamolodchikov–Bénard equations as hierarchy of isomonodromic deformations. Free fields approach" hep-th , 9709207 (1997) |
| [a53] | A. Levin, M. Olshanetsky, "Non-autonomous Hamiltonian systems related to highest Hitchin integrals" math-ph , 9904023 (1999) |
| [a54] | Y. Manin, "Frobenius manifolds, quantum cohomology and moduli spaces" , Colloq. Publ. , 47 , Amer. Math. Soc. (1999) MR1702284 Zbl 0952.14032 |
| [a55] | M. Mariño, "The uses of Whitham hierarchies" hep-th , 9905053 (1999) MR1747981 |
| [a56] | M. Mariño, G. Moore, "Integrating over the Coulomb branch in $N = 2$ gauge theory" hep-th , 9712062 (1997) Zbl 0959.57028 |
| [a57] | M. Mariño, G. Moore, "The Donaldson–Witten function for gaug groups of rank larger than one" hep-th , 9802185 (1998) |
| [a58] | M. Mariño, G. Moore, "Donaldson invariants for nonsingularly connected manifolds" hep-th , 9804104 (1998) |
| [a59] | G. Moore, E. Witten, "Integration over the $u$-plane in Donaldson theory" hep-th , 9709193 (1997) MR1605636 |
| [a60] | P.D. Miller, N.M. Ercolani, I.M. Krichever, C.D. Levermore, "Finite genus solutions to the Ablowitz–Ladik equations" Commun. Pure Appl. Math. , 48 (1996) pp. 1369–1440 MR1369393 Zbl 0869.34065 |
| [a61] | R. Miura, M. Kruskal, "Application of a nonlinear WKB method in Korteweg–de Vries equation" SIAM J. Appl. Math. , 26 (1974) pp. 376–395 |
| [a62] | T. Nakatsu, K. Takasaki, "Isomonodromic deformations and supersymmetric gauge theories" Int. J. Modern Phys. A , 11 (1996) pp. 5505–5518 MR1416437 Zbl 0985.81756 |
| [a63] | M. Olshanetsky, "Painlevé type equations and Hitchin systems" math-ph , 9901019 (1999) MR1816175 Zbl 0980.34086 |
| [a64] | M.V. Pavlov, "Nonlinear Schrödinger equation and the Bogolyubov–Whitham method of averaging" Theoret. Math. Phys. , 71 (1987) pp. 584–588 Zbl 0639.35013 |
| [a65] | G. Potemin, "Algebro-geometric consttruction of self-similar solutons of the Whitham equations" Russian Math. Surveys , 43 (1988) pp. 252–253 |
| [a66] | K. Takasaki, "Dual isomonodromic problems and Whitham equations" hep-th , 9700516 (1998) MR1607288 Zbl 0899.35109 |
| [a67] | K. Takasaki, "Dual isomonodromic problems and Whitham equations" Lett. Math. Phys. , 43 (1998) pp. 123–135 MR1607288 Zbl 0899.35109 |
| [a68] | K. Takasaki, "Spectral curves and Whitham equations in isomonodromic problems of Schlesinger type" solv-int , 9704004 (1997) MR1734137 Zbl 0959.34075 |
| [a69] | K. Takasaki, "Gaudin model, KZ equation, and isomonodromic problem on torus" hep-th , 9711058 (1997) Zbl 0944.37034 |
| [a70] | K. Takasaki, T. Nakatsu, "Isomonodromic deformations and supersymmetric gauge theories" Int. J. Modern Phys. A , 11 (1996) pp. 5505–5518 MR1416437 Zbl 0985.81756 |
| [a71] | K. Takasaki, "Integrable hierarchies and contact terms in $u$-plane integrals of topologically twisted supersymmetric gauge theories" Int. J. Modern Phys. A , 14 (1998) pp. 1001–1014 |
| [a72] | K. Takasaki, "Whitham deformations of Seiberg–Witten curves for classical gauge groups" Int. J. Modern Phys. A , 15 (2000) pp. 3635–3666 MR1781360 Zbl 0973.81036 |
| [a73] | S. Venakides, "The generation of modulated wavetrains in the solution of the Korteweg–de Vries equation" Commun. Pure Appl. Math. , 38 (1985) pp. 883–909 MR0812354 Zbl 0657.35110 |
| [a74] | G. Whitham, "Linear and nonlinear waves" , Wiley (1974) MR0483954 Zbl 0373.76001 |
| [a75] | G. Whitham, "Nonlinear dispersive waves" Proc. Royal Soc. A , 283 (1965) pp. 238–261 MR0205549 Zbl 0144.34803 |
 KSF
KSF