Witt vector
 From Encyclopedia of Mathematics - Reading time: 8 min
From Encyclopedia of Mathematics - Reading time: 8 min
An element of an algebraic construct, first proposed by E. Witt [1] in 1936 in the context of the description of unramified extensions of $ p $-
adic number fields. Witt vectors were subsequently utilized in the study of algebraic varieties over a field of positive characteristic [3], in the theory of commutative algebraic groups [4], [5], and in the theory of formal groups [6]. Let $ A $
be an associative, commutative ring with unit element. Witt vectors with components in $ A $
are infinite sequences $ a = (a _{0} , a _{1} , . . . ) $,
$ a _{i} \in A $,
which are added and multiplied in accordance with the following rules: $$
(a _{0} ,\ a _{1} ,\dots ) \dot{+}
(b _{0} ,\ b _{1} ,\dots ) =
$$
$$
=
(S _{0} (a _{0} ,\ b _{0} ),\ S _{1} (a _{0} ,\ a _{1} ; \ b _{0} ,\ b _{1} ) , . . . ),
$$
$$
(a _{0} ,\ a _{1} , . . . ) \dot \times (b _{0} ,\ b _{1} , . . . ) =
$$
$$
=
(M _{0} (a _{0} ,\ b _{0} ),\ M _{1} (a _{0} ,\ a _{1} ; \ b _{0} ,\ b _{1} ) , . . . ),
$$
where $ S _{n} $,
$ M _{n} $
are polynomials in the variables $ X _{0} \dots X _{n} $,
$ Y _{0} \dots Y _{n} $
with integer coefficients, uniquely defined by the conditions $$
\Phi _{n} (S _{0} \dots S _{n} ) =
\Phi _{n} (X _{0} \dots X _{n} ) +
\Phi _{n} (Y _{0} \dots Y _{n} ),
$$
$$
\Phi _{n} (M _{0} \dots M _{n} ) = \Phi _{n} (X _{0} \dots X _{n} ) \cdot \Phi _{n} (Y _{0} \dots Y _{n} );
$$
where $$
\Phi _{n} = Z _{0} ^ {p ^ n} + pZ _{1} ^ {p ^ n-1} + \dots
+ p ^{n} Z _{n} $$
are polynomials, $ n \in \mathbf N $
and $ p $
is a prime number. In particular, $$
S _{0} = X _{0} + Y _{0} ;
S _{1} = X _{1} + Y _{1} -
\sum _ {i = 1} ^ {p-1} {
\frac{1}{p}
}
\binom{p}{i}
X _{0} ^{i} Y _{0} ^{p-i} ;
$$
$$
M _{0} = X _{0} Y _{0} , M _{1} = X
_{0} ^{p} Y _{1} + X _{1} Y _{0} ^{p} + pX _{1} Y _{1} .
$$
The Witt vectors with the operations introduced above form a ring, called the ring of Witt vectors and denoted by $ W(A) $.
For any natural number $ n $
there also exists a definition of the ring $ W _{n} (A) $
of truncated Witt vectors of length $ n $.
The elements of this ring are finite tuples $ a = (a _{0} \dots a _{n-1} ) $,
$ a _{i} \in A $,
with the addition and multiplication operations described above. The canonical mappings $$
R: \ W _{n+1} (A) \rightarrow W _{n} (A),
$$
$$
R ((a _{0} \dots a _{n} )) = (a _{0} \dots a _{n-1} ) ,
$$
$$
T: \ W _{n} (A) \rightarrow W _{n+1} (A),
$$
$$
T ((a _{0} \dots a _{n-1} )) = (0,\ a _{0} \dots a _{n-1} ),
$$
are homomorphisms. The rule $ A \mapsto W(A) $(
or $ A \mapsto W _{n} (A) $)
defines a covariant functor from the category of commutative rings with unit element into the category of rings. This functor may be represented by the ring of polynomials $ \mathbf Z [X _{0} \dots X _{n} ,\dots ] $(
or $ \mathbf Z [X _{0} \dots X _{n-1} ] $)
on which the structure of a ring object has been defined. The spectrum $ \mathop{\rm Spec}\nolimits \ \mathbf Z [X _{0} \dots X _{n} ,\dots ] $(
or $ \mathop{\rm Spec}\nolimits \ \mathbf Z [X _{0} \dots X _{n-1} ] $)
is known as a Witt scheme (or a truncated Witt scheme) and is a ring scheme [3].
Each element $ a \in A $ defines a Witt vector $$ a ^ \tau = (a,\ 0,\ 0 , . . . ) \in W \ (A), $$ called the Teichmüller representative of the element $ a $. If $ A = k $ is a perfect field of characteristic $ p > 0 $, $ W(k) $ is a complete discrete valuation ring of zero characteristic with field of residues $ k $ and maximal ideal $ pW(k) $. Each element $ \omega \in W(k) $ can be uniquely represented as $$ \omega = \omega _{0} ^ \tau + p \omega _{1} ^ \tau + p ^{2} \omega _{2} ^ \tau + \dots , $$ where $ \omega _{i} \in k $. Conversely, each such ring $ A $ with field of residues $ k = A/p $ is canonically isomorphic to the ring $ W(k) $. The Teichmüller representation makes it possible to construct a canonical multiplicative homomorphism $ k \rightarrow W(k) $, splitting the mapping $$ W (k) \rightarrow W (k) / p \simeq k. $$ If $ k = \mathbf F _{p} $ is the prime field of $ p $ elements, $ W( \mathbf F _{p} ) $ is the ring of integral $ p $- adic numbers $ \mathbf Z _{p} $.
References[edit]
| [1] | E. Witt, "Zyklische Körper und Algebren der characteristik 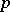 vom Grad vom Grad 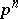 . Struktur diskret bewerteter perfekter Körper mit vollkommenem Restklassen-körper der Charakteristik . Struktur diskret bewerteter perfekter Körper mit vollkommenem Restklassen-körper der Charakteristik 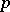 " J. Reine Angew. Math. , 176 (1936) pp. 126–140 Zbl 0016.05101 " J. Reine Angew. Math. , 176 (1936) pp. 126–140 Zbl 0016.05101 |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1974) MR0783636 Zbl 0712.00001 |
| [3] | D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) MR0209285 Zbl 0187.42701 |
| [4] | J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959) MR0103191 |
| [5] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , North-Holland (1971) MR1611211 MR0302656 MR0284446 Zbl 0223.14009 Zbl 0203.23401 Zbl 0134.16503 |
| [6] | J. Dieudonné, "Groupes de Lie et hyperalgèbres de Lie sur un corps de charactéristique 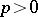 VII" Math. Ann. , 134 (1957) pp. 114–133 VII" Math. Ann. , 134 (1957) pp. 114–133 |
Comments[edit]
There is a generalization of the construction above which works for all primes $ p $ simultaneously, [a3]: a functor $ W : \ \mathbf{Ring} \rightarrow \mathbf{Ring} $ called the big Witt vector. Here, $ \mathbf{Ring} $ is the category of commutative, associative rings with unit element. The functor described above, of Witt vectors of infinite length associated to the prime $ p $, is a quotient of $ W $ which can be conveniently denoted by $ W _ {p ^ \infty} $.
For each $ n \in \{ 1,\ 2,\dots \} $,
let $ w _{n} (X) $
be the polynomial $$
w _{n} (X) = \sum _{d\mid n} dX _{d} ^{n/d} .
$$
Then there is the following characterization theorem for the Witt vectors. There is a unique functor $ W : \ \mathbf{Ring} \rightarrow \mathbf{Ring} $
satisfying the following properties: 1) as a functor $ W: \ \mathbf{Ring} \rightarrow \mathop{\rm Set}\nolimits $,
$ W (A) = \{ {(a _{1} ,\ a _{2} , \dots )} : {a _{i} \in A} \} $
and $ W ( \phi ) (a _{1} ,\ a _{2} , . . ) = ( \phi (a _{1} ) ,\ \phi (a _{2} ) ,\dots ) $
for any ring homomorphism $ \phi : \ A \rightarrow B $;
2) $ w _ {n , A} : \ W(A) \rightarrow A $,
$ ( a _{1} ,\ a _{2} ,\dots ) \mapsto w _{n} (a _{1} ,\ a _{2} ,\dots ) $
is a functorial homomorphism of rings for every $ A $
and $ n \in \{ 1,\ 2,\dots \} $.
The functor $ W $
admits functorial ring endomorphisms $ \mathbf f _{n} : \ W \rightarrow W $,
for every $ n \in \{ 1,\ 2,\dots \} $,
that are uniquely characterized by $ w _{n} \mathbf f _{m} = w _{nm} $
for all $ n,\ m \in \{ 1,\ 2,\dots \} $.
Finally, there is a functorial homomorphism $ \Delta : \ W(-) \rightarrow W(W(-)) $
that is uniquely characterized by the property $ w _ {n, W(A)} \Delta _{A} = \mathbf f _ {n, A} $
for all $ n $,
$ A $.
To construct $ W(A) $,
define polynomials $ \Sigma _{1} \dots \Sigma _{n} ,\dots $;
$ \Pi _{1} \dots \Pi _{n} ,\dots $;
$ r _{1} \dots r _{n} ,\dots $
by the requirements $$
w _{n} ( \Sigma _{1} \dots \Sigma _{n} ) =
w _{n} (X) + w _{n} (Y),
$$
$$
w _{n} ( \Pi _{1} \dots \Pi _{n} ) = w _{n} (X) w _{n} (Y),
$$
$$
w _{n} ( r _{1} \dots r _{n} ) = - w _{n} ( X) .
$$
The $ \Sigma _{n} $
and $ \Pi _{n} $
are polynomials in $ X _{1} \dots X _{n} $;
$ Y _{1} \dots Y _{n} $
and the $ r _{n} $
are polynomials in the $ X _{1} \dots X _{n} $
and they all have integer coefficients. $ W(A) $
is now defined as the set $ W(A) = \{ {\mathbf a = (a _{1} ,\ a _{2} ,\dots )} : {a _{i} \in A} \} $
with addition, multiplication and "minus" : $$
(a _{1} ,\ a _{2} ,\dots ) +
(b _{1} ,\ b _{2} ,\dots ) =
( \Sigma _{1} ( \mathbf a ) ,\ \Sigma _{2} ( \mathbf a ) ,\dots )
$$
$$
(a _{1} ,\ a _{2} ,\dots ) (b _{1} ,\ b _{2} ,\dots )
= ( \Pi _{1} ( \mathbf a ) ,\ \Pi _{2} ( \mathbf a ) ,\dots ) -
$$
$$
-
(a _{1} ,\ a _{2} ,\dots ) = ( r _{1} ( \mathbf a ) ,\ r _{2} ( \mathbf a ) ,\dots ) .
$$
The zero of $ W(A) $
is $ ( 0,\ 0 ,\dots ) $
and the unit element is $ ( 1,\ 0 ,\ 0 ,\dots ) $.
The Frobenius endomorphisms $ \mathbf f _{n} $
and the Artin–Hasse exponential $ \Delta $
are constructed by means of similar considerations, i.e. they are also given by certain universal polynomials. In addition there are the Verschiebung morphisms $ \mathbf V _{n} : \ W(-) \rightarrow W(-) $,
which are characterized by $$
w _{m} \mathbf V _{n} = \left \{
\begin{array}{ll}
0 & \textrm{ if } n \textrm{ does not divide } m, \\
nw _{m/n} & \textrm{ if } n \textrm{ divides } m. \\
\end{array}
\right .$$
The $ \mathbf V _{m} $
are group endomorphisms of $ W(-) $
but not ring endomorphisms.
The ideals $ I _{n} = \{ ( 0 \dots 0,\ a _{n+1} ,\ a _{n+2} ,\dots ) \} \subset W(A) $ define a topology on $ W(A) $ making $ W(A) $ a separated complete topological ring.
For each $ A \in \mathbf{Ring} $, let $ \Lambda (A) $ be the Abelian group $ 1 + t A [[t]] $ under multiplication of power series; $$ \overline{E}\; : \ W(A) \rightarrow \Lambda (A), $$ $$ ( a _{1} ,\ a _{2} ,\dots ) \mapsto \prod _{i=1} ^ \infty (1- a _{i} t ^{i} ) , $$ defines a functional isomorphism of Abelian groups, and using the isomorphism $ \overline{E}\; $ there is a commutative ring structure on $ \Lambda (A) $. Using $ \overline{E}\; $ the Artin–Hasse exponential $ \Delta $ defines a functorial homomorphism of rings $$ W(A) \rightarrow \Lambda (W(A)) $$ making $ W(A) $ a functorial special $ \lambda $- ring. The Artin–Hasse exponential $ \Delta : \ W \rightarrow W \circ W $ defines a cotriple structure on $ W $ and the co-algebras for this co-triple are precisely the special $ \lambda $- rings (cf. also Category and Triple).
On $ \Lambda (A) $ the Frobenius and Verschiebung endomorphisms satisfy $$ \mathbf f _{n} (1-at) = (1-a ^{n} t) , $$ $$ \mathbf V _{n} f(t) = f(t ^{n} ) , $$ and are completely determined by this (plus functoriality and additivity in the case of $ \mathbf f _{n} $).
For each supernatural number $ \mathbf n = \prod _{p} p ^ {\alpha _ p} $,
$ \alpha _{p} \in \{ 0,\ 1,\ 2,\dots \} \cup \{ \infty \} $,
one defines $ N ( \mathbf n ) = \{ {n \in \{ 1,\ 2,\dots \}} : {v _{p} (n) \leq \alpha _{p } \textrm{ for all "prime" numbers } p} \} $,
where $ v _{p} $
is the $ p $-
adic valuation of $ n $,
i.e. the number of prime factors $ p $
in $ n $.
Let $$
\mathfrak a _ {\mathbf n} (A) =
$$
$$
=
\{ {(a _{1} ,\ a _{2} ,\dots )} : {
a _{d} = 0 \textrm{ for all } d \in N ( \mathbf n )} \} .
$$
Then $ \mathfrak a _ {\mathbf n} (A) $
is an ideal in $ W(A) $
and for each supernatural $ \mathbf n $
a corresponding ring of Witt vectors is defined by $$
W _ {\mathbf n} (A) = W(A) / \mathfrak a _ {\mathbf n} (A) .
$$
In particular, one thus finds $ W _ {p ^ \infty} (A) $,
the ring of infinite-length Witt vectors for the prime $ p $,
discussed in the main article above, as a quotient of the ring of big Witt vectors $ W(A) $.
The Artin–Hasse exponential $ \Delta : \ W \rightarrow W \circ W $
is compatible in a certain sense with the formation of these quotients, and using also the isomorphism $ \overline{E}\; $
one thus finds a mapping $$
\mathbf Z _{p} = W _ {p ^ \infty} ( \mathbf F _{p} ) \rightarrow
\Lambda (W _ {p ^ \infty} ( \mathbf F _{p} ) ) =
\Lambda ( \mathbf Z _{p} ) ,
$$
where $ \mathbf Z _{p} $
denotes the $ p $-
adic integers and $ \mathbf F _{p} $
the field of $ p $
elements, which can be identified with the classical morphism defined by Artin and Hasse [a1], [a2], [a3].
As an Abelian group $ W(A) $ is isomorphic to the group of curves $ {\mathcal C} ( \mathbf G _{m} ; \ A) $ of curves in the one-dimensional multiplicative formal group $ \mathbf G _{m} $. In this way there is a Witt-vector-like Abelian-group-valued functor associated to every one-dimensional formal group. For special cases, such as the Lubin–Tate formal groups, this gives rise to ring-valued functors called ramified Witt vectors, [a3], [a4].
Let $ r _{n} (X,\ Y) $ be the sequence of polynomials with coefficients in $ \mathbf Z $ defined by $$ X ^{n} + Y ^{n} = \sum _{d\mid n} d r _{d} (X,\ Y) ^{n/d} . $$ The Cartier ring $ \mathop{\rm Cart}\nolimits (A) $ is the ring of all formal expressions $$ \tag{*} \sum _ {i,j \in \{ 1, 2,\dots \}} \mathbf V _{i} \langle a _{ij} \rangle \mathbf f _{j} $$ with the calculation rules $$ \langle a><b\rangle = \langle ab\rangle , \langle 1\rangle = \mathbf f _{1} = \mathbf V _{1} = \textrm{ unit element } 1 , $$ $$ \mathbf V _{n} \mathbf V _{m} = \mathbf V _{nm} , \mathbf f _{n} \mathbf f _{m} = \mathbf f _{nm} , $$ $$ \langle a\rangle \mathbf V _{m} = \mathbf V _{m} \langle a ^{m} \rangle , \mathbf f _{m} \langle a\rangle = \langle a ^{m} \rangle \mathbf f _{m} , $$ $$ \mathbf V _{m} \mathbf f _{n} = \mathbf f _{n} \mathbf V _{m} \textrm{ if } (n,\ m) = 1 , $$ $$ \mathbf f _{n} \mathbf V _{n} = 1 + \dots + 1 ( n \textrm{ summands } ) , $$ $$ \langle a+b\rangle = \sum _{n=1} ^ \infty \mathbf V _{n} \langle r _{n} ( a,\ b) \rangle \mathbf f _{n} . $$ Commutative formal groups over $ A $ are classified by certain modules over $ \mathop{\rm Cart}\nolimits (A) $. In case $ A $ is a $ \mathbf Z _{(p)} $- algebra, a simpler ring $ \mathop{\rm Cart}\nolimits _{p} (A) $ can be used for this purpose. It consists of all expressions (*) where now the $ i,\ j $ only run over the powers $ p ^{0} ,\ p ^{1} ,\ p ^{2} , . . . $ of the prime $ p $. The calculation rules are the analogous ones. In case $ k $ is a perfect field of characteristic $ p > 0 $ and $ \sigma $ denotes the Frobenius endomorphism of $ W(k) $( which in this case is given by $ \sigma ( a _{1} ,\ a _{2} , . . . ) = ( a _{1} ^{p} ,\ a _{2} ^{p} , . . ) $), then $ \mathop{\rm Cart}\nolimits _{p} (k) $ can be described as the ring of all expressions $$ x _{0} + \sum _{i=1} ^ \infty x _{i} \mathbf V ^{i} + \sum _{j=1} ^ \infty y _{j} \mathbf f ^{i} , $$ in two symbols $ \mathbf f $ and $ \mathbf V $ and with coefficients in $ W _ {p ^ \infty} (k) $, with the extra condition $ \mathop{\rm lim}\nolimits _ {i \rightarrow \infty} \ y _{i} = 0 $ and the calculation rules $$ \mathbf f x = \sigma (x) \mathbf f , \mathbf V x = \sigma ^{-1} (x) \mathbf V , $$ $$ \mathbf f \mathbf V = \mathbf V \mathbf f = p . $$ This ring, and also its subring of all expressions $$ x _{0} + \sum _{i=1} ^ \infty x _{i} \mathbf V ^{i} + \sum _{j=1} ^ {< \infty} y _{j} \mathbf f ^{j} , $$ is known as the Dieudonné ring $ D(k) $ and certain modules (called Dieudonné modules) over it classify unipotent commutative affine group schemes over $ k $, cf. [a5].
References[edit]
| [a1] | E. Artin, H. Hasse, "Die beide Ergänzungssätze zum Reciprozitätsgesetz der 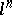 -ten Potenzreste im Körper der -ten Potenzreste im Körper der 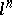 -ten Einheitswurzeln" Abh. Math. Sem. Univ. Hamburg , 6 (1928) pp. 146–162 -ten Einheitswurzeln" Abh. Math. Sem. Univ. Hamburg , 6 (1928) pp. 146–162 |
| [a2] | G. Whaples, "Generalized local class field theory III: Second form of the existence theorem, structure of analytic groups" Duke Math. J. , 21 (1954) pp. 575–581 MR73645 |
| [a3] | M. Hazewinkel, "Twisted Lubin–Tate formal group laws, ramified Witt vectors and (ramified) Artin–Hasse exponentials" Trans. Amer. Math. Soc. , 259 (1980) pp. 47–63 MR0561822 Zbl 0437.13014 |
| [a4] | M. Hazewinkel, "Formal group laws and applications" , Acad. Press (1978) MR506881 |
| [a5] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , North-Holland (1971) MR1611211 MR0302656 MR0284446 Zbl 0223.14009 Zbl 0203.23401 Zbl 0134.16503 |
 KSF
KSF