24 (number)
 From HandWiki - Reading time: 8 min
From HandWiki - Reading time: 8 min
Short description: Natural number
| ||||
|---|---|---|---|---|
| Cardinal | twenty-four | |||
| Ordinal | 24th (twenty-fourth) | |||
| Numeral system | tetravigesimal | |||
| Factorization | 23 × 3 | |||
| Divisors | 1, 2, 3, 4, 6, 8, 12, 24 | |||
| Greek numeral | ΚΔ´ | |||
| Roman numeral | XXIV | |||
| Binary | 110002 | |||
| Ternary | 2203 | |||
| Quaternary | 1204 | |||
| Quinary | 445 | |||
| Senary | 406 | |||
| Octal | 308 | |||
| Duodecimal | 2012 | |||
| Hexadecimal | 1816 | |||
| Vigesimal | 1420 | |||
| Base 36 | O36 | |||
24 (twenty-four) is the natural number following 23 and preceding 25.
In mathematics
24 is an even composite number, with 2 and 3 as its distinct prime factors. It is the first number of the form 2qq, where q is an odd prime. It is the smallest number with at least eight positive divisors: 1, 2, 3, 4, 6, 8, 12, and 24;[1] thus, it is a highly composite number, having more divisors than any smaller number.[2] Furthermore, it is an abundant number, since the sum of its proper divisors (36) is greater than itself, as well as a superabundant number.
In number theory and algebra
- 24 is the smallest 5-hemiperfect number, as it has a half-integer abundancy index:
- 1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 = 60 = 5/2 × 24
- 24 is a semiperfect number, since adding up all the proper divisors of 24 except 4 and 8 gives 24.[3]
- 24 is a practical number, since all smaller positive integers than 24 can be represented as sums of distinct divisors of 24.
- 24 is a Harshad number, since it is divisible by the sum of its digits in decimal.[4]
- 24 is a refactorable number, as it has exactly eight positive divisors, and 8 is one of them.
- 24 is a twin-prime sum, specifically the sum of the third pair of twin primes .
- 24 is a highly totient number, as there are 10 solutions to the equation φ(x) = 24, which is more than any integer below 24. 144 (the square of 12) and 576 (the square of 24) are also highly totient.[5]
- 24 is a polite number, an amenable number, an idoneal number, and a tribonacci number.
- 24 forms a Ruth-Aaron pair with 25, since the sums of distinct prime factors of each are equal (5).
- 24 is a compositorial, as it is the product of composite numbers up to 6.
- 24 is a pernicious number, since its Hamming weight in its binary representation (11000) is prime (2).
- 24 is the third nonagonal number.[6]
- 24's digits in decimal can be manipulated to form two of its factors, as 2 * 4 is 8 and 2 + 4 is 6. In turn 6 * 8 is 48, which is twice 24, and 4 + 8 is 12, which is half 24.
- 24 is a congruent number, as 24 is the area of a right triangle with a rational number of sides.
- 24 is a semi-meandric number, where an order-6 semi-meander intersects an oriented ray in R2 at 24 points.
- 24 is the number of digits of the fifth and largest known unitary perfect number, when written in decimal: 146361946186458562560000.[7]
- Subtracting 1 from any of its divisors (except 1 and 2 but including itself) yields a prime number; 24 is the largest number with this property.
- 24 is the largest integer that is divisible by all natural numbers no larger than its square root.
- The product of any four consecutive numbers is divisible by 24. This is because, among any four consecutive numbers, there must be two even numbers, one of which is a multiple of four, and there must be at least one multiple of three.
- 24 = 4!, the factorial of 4. It is the largest factorial that does not contain a trailing zero at the end of its digits (since factorial of any integer greater than 4 is divisible by both 2 and 5), and represents the number of ways to order 4 distinct items:
- (1,2,3,4), (1,2,4,3), (1,3,2,4), (1,3,4,2), (1,4,2,3), (1,4,3,2), (2,1,3,4), (2,1,4,3), (2,3,1,4), (2,3,4,1), (2,4,1,3), (2,4,3,1), (3,1,2,4), (3,1,4,2), (3,2,1,4), (3,2,4,1), (3,4,1,2), (3,4,2,1), (4,1,2,3), (4,1,3,2), (4,2,1,3), (4,2,3,1), (4,3,1,2), (4,3,2,1).
- 24 is the only nontrivial solution to the cannonball problem; that is, 12 + 22 + 32 + … + 242 is a perfect square (702).[8]
- 24 is the only number whose divisors — 1, 2, 3, 4, 6, 8, 12, 24 — are exactly those numbers n for which every invertible element of the commutative ring Z/nZ is a square root of 1. It follows that the multiplicative group of invertible elements (Z/24Z)× = {±1, ±5, ±7, ±11} is isomorphic to the additive group (Z/2Z)3. This fact plays a role in monstrous moonshine.
- It follows that any number n relatively prime to 24 (that is, any number of the form 6K ± 1), and in particular any prime n greater than 3, has the property that n2 – 1 is divisible by 24.
- The modular discriminant Δ(τ) is proportional to the 24th power of the Dedekind eta function η(τ): Δ(τ) = (2π)12η(τ)24.
In geometry
- 24 degrees is the measure of the central angle and external angle of a pentadecagon.
- An icositetragon is a regular polygon with 24 sides and Dih24 symmetry of order 48. It can fill a plane-vertex alongside a triangle and octagon.
- 24 is the Euler characteristic of a K3 surface: a general elliptic K3 surface has exactly 24 singular fibers.
- 24 is the order of the octahedral group — the group of rotations of the regular octahedron and the group of rotations of the cube. The binary octahedral group is a subgroup of the 3-sphere S3 consisting of the 24 elements {±1, ±i, ±j, ±k, (±1±i±j±k)/2} of the binary tetrahedral group along with the 24 elements contained in its coset {(±1±i)/√2, (±1±j)/√2, (±1±k)/√2, (±i±j)/√2, (±i±k)/√2, (±j±k)/√2}. These two cosets each form the vertices of a self-dual 24-cell, and the two 24-cells are dual to each other. (See point below on 24-cell).
- 24 is the count of different elements in various uniform polyhedron solids. Within the family of Archimedean and Catalan solids, there are 24 edges in a cuboctahedron and rhombic dodecahedron, 24 vertices in a rhombicuboctahedron, truncated cube, truncated octahedron, and snub cube, as well as 24 faces in a deltoidal icositetrahedron, tetrakis hexahedron, triakis octahedron, and pentagonal icositetrahedron. The cube-octahedron compound, with a rhombic dodecahedral convex hull, is the first stellation of the cuboctahedron, with a total of 24 edges.
- There are 12 non-prismatic uniform polyhedron compounds (UC01, UC03, UC08, UC10, UC12, UC30, UC42, UC46, UC48, UC50, UC52, and UC54) and 12 uniform star polyhedra (U03, U13, U14, U15, U17, U18, U19, U21, U36, U37, U41, and U58) with a vertex, edge, or face count of 24. The great disnub dirhombidodecahedron, also called Skilling's figure, is a degenerate uniform star polyhedron with a Euler characteristic of 24, when pairs of coinciding edges are considered to be single edges.
- Finally, 6 Johnson solids (J17, J27, J37, J45, J61, and J90) also have vertex, edge, or face counts of 24. The pseudo great rhombicuboctahedron, one of two known pseudo-uniform polyhedra alongside the elongated square gyrobicupola (J37), has 24 vertices.
- The tesseract has 24 two-dimensional faces (which are all squares). Its dual four-dimensional polytope is the 16-cell, which has 24 edges.
- The 24-cell, with 24 octahedral cells and 24 vertices, is a self-dual convex regular 4-polytope. It possesses 576 (24×24) rotational symmetries and 1152 isometries altogether. It tiles 4-dimensional space in a 24-cell honeycomb, in which each 24-cell is surrounded by 24 24-cells.
- The vertices of the 24-cell honeycomb can be chosen so that in 4-dimensional space, identified with the ring of quaternions, they are precisely the elements of the subring (the ring of "Hurwitz integral quaternions") generated by the binary tetrahedral group as represented by the set of 24 quaternions in the D4 lattice. This set of 24 quaternions forms the set of vertices of a single 24-cell, all lying on the sphere S3 of radius one centered at the origin. S3 is the Lie group Sp(1) of unit quaternions (isomorphic to the Lie groups SU(2) and Spin(3)), and so the binary tetrahedral group — of order 24 — is a subgroup of S3.
- The 24 vertices of the 24-cell are contained in the regular complex polygon 4{3}4,
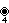

 or
or 

 of symmetry order 1152, as well as 24 4-edges of 24 octahedral cells (of 48). Its representation in the F4 Coxeter plane contains two rings of 12 vertices each.[9]
of symmetry order 1152, as well as 24 4-edges of 24 octahedral cells (of 48). Its representation in the F4 Coxeter plane contains two rings of 12 vertices each.[9] - Truncations, runcinations, and omnitruncations of the 24-cell yield 4-dimensional polytopes whose Petrie polygons are 24-sided icositetragons; i.e., within the truncated 24-cell, runcinated 24-cell, and omnitruncated 24-cell, amongst others.
- 24 is the kissing number in 4-dimensional space: the maximum number of unit spheres that can all touch another unit sphere without overlapping. (The centers of 24 such spheres form the vertices of a 24-cell).
- The Barnes–Wall lattice contains 24 lattices.
- In 24 dimensions there are 24 even positive definite unimodular lattices, called the Niemeier lattices. One of these is the exceptional Leech lattice which has many surprising properties; due to its existence, the answers to many problems such as the kissing number problem and densest lattice sphere-packing problem are known in 24 dimensions but not in many lower dimensions. The Leech lattice is closely related to the equally nice length-24 binary Golay code and the Steiner system S(5,8,24) and the Mathieu group M24. (One construction of the Leech lattice is possible because 12 + 22 + 32 + ... + 242 = 702.)
- 24 is the order of the cyclic group equal to the stable 3-stem in homotopy groups of spheres: πn+3(Sn) = Z/24Z for all n ≥ 5.
In science
- The atomic number of chromium.[10]
- The average number of hours in a day (on Earth), also known as a mean solar day.
- 24! is an approximation (exceeding by just over 3%) of the Avogadro constant.
In religion
- The number of books in the Tanakh.
- In Christian apocalyptic literature it represents the complete Church, being the sum of the 12 tribes of Israel and the 12 Apostles of the Lamb of God. For example, in The Book of Revelation: "Surrounding the throne were twenty-four other thrones, and seated on them were twenty-four elders. They were dressed in white and had crowns of gold on their heads."[11]
- Number of Tirthankaras in Jainism.
- Number of spokes in the Ashok Chakra.
In music
- There are a total of 24 major and minor keys in Western tonal music, not counting enharmonic equivalents. Therefore, for collections of pieces written in each key, the number of pieces in such a collection; e.g., Chopin's 24 Preludes.
In sports
- Four-and-Twenty was an American racehorse.
- In association football:
- The FIFA World Cup final tournament featured 24 men's national teams from 1982 to 1994.
- The FIFA Women's World Cup final tournament featured 24 national teams in 2015 and 2019.
- In basketball:
- In the NBA, the time on a shot clock is 24 seconds.
- In NASCAR, the number 24 has found the most success with Jeff Gordon and Hendrick Motorsports, winning the 1995, 1997, 1998, and 2001 NASCAR Winston Cup Series championships and 93 races (including the 1997, 1999, and 2005 Daytona 500). It is currently used by driver William Byron.
In other fields

24 is also:
- The number of bits a computer needs to represent 24-bit color images (for a maximum of 16,777,216 colours—but greater numbers of bits provide more accurate colors).
- The number of karats representing 100% pure gold.[12]
- The number of cycles in the Chinese solar year.
- The number of years from the start of the Cold War until the signing of the Seabed Arms Control Treaty, which banned the placing of nuclear weapons on the ocean floor within certain coastal distances.
- The number of frames per second at which motion picture film is usually projected, as this is sufficient to allow for persistence of vision.
- The number of letters in both the modern and classical Greek alphabet.[13] For the latter reason, also the number of chapters or "books" into which Homer's Odyssey and Iliad came to be divided.
- The number of runes in the Elder Futhark.
- The number of points on a backgammon board.[14]
- A children's mathematical game involving the use of any of the four standard operations on four numbers on a card to get 24 (see 24 Game).
- The maximum number of Knight Companions in the Order of the Garter.
- The number of the French department Dordogne.
- Four and twenty is the number of blackbirds baked in a pie in the traditional English nursery rhyme "Sing a Song of Sixpence".
- In Brazil , twenty-four is associated with homosexuality as it is the number that stands for the deer in a game known as “jogo do bicho”.
References
- ↑ Sloane, N. J. A., ed. "Sequence A005179 (Smallest number with exactly n divisors.)". OEIS Foundation. https://oeis.org/A005179. Retrieved 2023-11-06.
- ↑ "Sloane's A002182 : Highly composite numbers". OEIS Foundation. https://oeis.org/A002182.
- ↑ "Sloane's A005835 : Pseudoperfect (or semiperfect) numbers". OEIS Foundation. https://oeis.org/A005835.
- ↑ "Sloane's A005349 : Niven (or Harshad) numbers". OEIS Foundation. https://oeis.org/A005349.
- ↑ "Sloane's A097942 : Highly totient numbers". OEIS Foundation. https://oeis.org/A097942.
- ↑ "Sloane's A001106 : 9-gonal (or enneagonal or nonagonal) numbers". OEIS Foundation. https://oeis.org/A001106.
- ↑ Sloane, N. J. A., ed. "Sequence A002827 (Unitary perfect numbers)". OEIS Foundation. https://oeis.org/A002827. Retrieved 2023-01-10.
- ↑ Weisstein, Eric W.. "Cannonball Problem" (in en). https://mathworld.wolfram.com/CannonballProblem.html.
- ↑ Coxeter, H.S.M. (1991), Regular Complex Polytopes (2nd ed.), Cambridge: Cambridge University Press
- ↑ Meija, Juris; Coplen, Tyler B.; Berglund, Michael; Brand, Willi A.; Bièvre, Paul De; Gröning, Manfred; Holden, Norman E.; Irrgeher, Johanna et al. (2016-03-01). "Atomic weights of the elements 2013 (IUPAC Technical Report)" (in en). Pure and Applied Chemistry 88 (3): 265–291. doi:10.1515/pac-2015-0305. ISSN 0033-4545. https://www.degruyter.com/view/journals/pac/88/3/article-p265.xml.
- ↑ "Revelation 4:4, New International Version (1984)". Bible.cc. http://bible.cc/revelation/4-4.htm.
- ↑ "Is 24K gold pure?" (in en). https://www.scientificamerican.com/article/is-24k-gold-pure/.
- ↑ "Greek alphabet | History, Definition, & Facts" (in en). https://www.britannica.com/topic/Greek-alphabet.
- ↑ "GammonSite - Rules of backgammon". https://www.gammonsite.com/bgrules.aspx.
External links
 |
Licensed under CC BY-SA 3.0 | Source: https://handwiki.org/wiki/24_(number)190 views | Status: cached on January 19 2026 12:58:39↧ Download this article as ZWI file
 KSF
KSF