65 (number)
 From HandWiki - Reading time: 3 min
From HandWiki - Reading time: 3 min
| ||||
|---|---|---|---|---|
| Cardinal | sixty-five | |||
| Ordinal | 65th (sixty-fifth) | |||
| Factorization | 5 × 13 | |||
| Divisors | 1, 5, 13, 65 | |||
| Greek numeral | ΞΕ´ | |||
| Roman numeral | LXV | |||
| Binary | 10000012 | |||
| Ternary | 21023 | |||
| Quaternary | 10014 | |||
| Quinary | 2305 | |||
| Senary | 1456 | |||
| Octal | 1018 | |||
| Duodecimal | 5512 | |||
| Hexadecimal | 4116 | |||
| Vigesimal | 3520 | |||
| Base 36 | 1T36 | |||
65 (sixty-five) is the natural number following 64 and preceding 66.
In mathematics
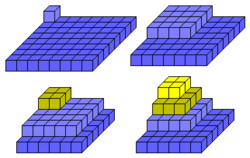
65 is the nineteenth distinct semiprime,[1] (5.13); and the third of the form (5.q), where q is a higher prime.
65 has a prime aliquot sum of 19 within an aliquot sequence of one composite numbers (65,19,1,0) to the prime; as the first member' of the 19-aliquot tree.
It is an octagonal number.[2] It is also a Cullen number.[3] Given 65, the Mertens function returns 0.[4]
This number is the magic constant of a 5x5 normal magic square:
This number is also the magic constant of n-Queens Problem for n = 5.[5]
65 is the smallest integer that can be expressed as a sum of two distinct positive squares in two (or more) ways, 65 = 82 + 12 = 72 + 42.[6]
It appears in the Padovan sequence, preceded by the terms 28, 37, 49 (it is the sum of the first two of these).[7]
65 is a Stirling number of the second kind, the number of ways of dividing a set of six objects into four non-empty subsets.[8]
65 = 15 + 24 + 33 + 42 + 51.[9]
65 is the length of the hypotenuse of 4 different Pythagorean triangles, the lowest number to have more than 2: 652 = 162 + 632 = 332 + 562 = 392 + 522 = 252 + 602.[10] The first two are "primitive", and 65 is the lowest number to be the largest side of more than one such triple.[11]
65 is the number of compositions of 11 into distinct parts.[12]
In science
- The atomic number of terbium, a lanthanide
Astronomy
- Messier object M65, a galaxy of magnitude 10.5 in the constellation Leo
- The New General Catalogue object NGC 65, a spiral galaxy in the constellation Cetus
In music
- "65 Love Affair", singer Paul Davis' hit song in 1982
- Sammy Hagar re-recorded his hit "I Can't Drive 55", with the 55 changed to 65, in 2001 for NBC's NASCAR broadcasts to reflect higher speed limits; the song was used from 2001 until 2004 to introduce Budweiser Pole Award winners on NBC and TNT broadcasts
- 65 is a commonly used abbreviation for the Sheffield, UK, post-rock band 65daysofstatic
- Referenced in "Heroes and Villains" by the Beach Boys: "At 60 and 5 / I'm very much alive / I've still got the jive / to survive with the Heroes and Villains"
- Odd Future group MellowHype has performed a song entitled "65"
In other fields
- 65 miles per hour is a common speed limit on expressways in many U.S. states, primarily in the eastern and central United States. (In the western United States, a common speed limit is 70 m.p.h., and in some places it is 75 m.p.h.).
- +65 is the code for international direct dial telephone calls to Singapore.
- the traditional age for retirement in the United Kingdom, Germany, the United States, Canada, and several other countries.
- in the U.S., the age at which a person is eligible to obtain Medicare.
- CVN-65 is the designation of the U.S. Navy's first nuclear-powered aircraft carrier, the USS Enterprise (CVN-65).
- 65 is the minimum grade or average required to pass an exam, or a class, in some schools.
- The setting of the American classic TV series Naked City (1958–1963) was the 65th Precinct in New York City (sometimes referred to as simply "the 65").
- 65 is the number of the French department Hautes-Pyrénées.
- 65 is commonly used in names of many dishes of South India cuisine, for instance Chicken 65.
- The M-65 field jacket was commonly worn by American troops during the War in Vietnam.
- A 65th anniversary is sometimes referred to as a sapphire jubilee.
- The AGM-65 Maverick is a mass-produced air-to-ground tactical missile (AGM) designed for close air support against a wide range of targets.
References
- ↑ Sloane, N. J. A., ed. "Sequence A001358". OEIS Foundation. https://oeis.org/A001358.
- ↑ "Sloane's A000567 : Octagonal numbers". OEIS Foundation. https://oeis.org/A000567.
- ↑ "Sloane's A002064 : Cullen numbers". OEIS Foundation. https://oeis.org/A002064.
- ↑ "Sloane's A028442 : Numbers n such that Mertens' function is zero". OEIS Foundation. https://oeis.org/A028442.
- ↑ Sloane, N. J. A., ed. "Sequence A006003". OEIS Foundation. https://oeis.org/A006003.
- ↑ OEIS: A024508
- ↑ "Sloane's A000931 : Padovan sequence". OEIS Foundation. https://oeis.org/A000931.
- ↑ "Sloane's A008277 : Triangle of Stirling numbers of the second kind". OEIS Foundation. https://oeis.org/A008277.
- ↑ OEIS: A003101
- ↑ OEIS: A164282
- ↑ OEIS: A024409
- ↑ Sloane, N. J. A., ed. "Sequence A032020 (Number of compositions (ordered partitions) of n into distinct parts)". OEIS Foundation. https://oeis.org/A032020. Retrieved 2022-05-24.
 |
 KSF
KSF