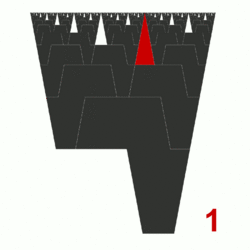
Africa (fractal)

Africa is a fractal made of a set of octagons that have some resemblance to the shape of Africa.^[1][2][3] The number of octagons of different sizes in the fractal is related to the Fibonacci sequence: 1, 2, 3, 5, 8, 13, 21, .... The height of the largest octagon of the fractal is φ times longer than that of the second octagon; where φ is the golden ratio.^[4][5][6]

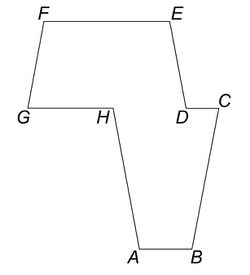
The original version of the fractal was defined by the octagon with the following vertices:^[7]

The following relations are obvious and necessary based on the shape of fractal:

${\displaystyle c_1-b_1=a_1-h_1}$

${\displaystyle d_1-e_1=f_1-g_1}$

${\displaystyle c_2-b_2=h_2-a_2}$

${\displaystyle e_2-d_2=f_2-g_2}$

${\displaystyle \frac{b_1-a_1}{c_1-d_1}=\frac{c_1-b_1}{d_1-e_1}=\frac{c_2-b_2}{e_2-d_2}=\frac{1+\sqrt{5}}{2}=\phi }$

${\displaystyle \frac{2(h_1-g_1)}{\phi }+\frac{b_1-a_1}{{\phi }^2}=e_1-f_1}$

where φ is the golden ratio. The fractal is made up of a countable number of copies of the octagon and its lateral inversion. The octagon has some resemblance to the shape of Africa:

The shape of the fractal can form the following tessellations:^[8]

In the fractal, the number of octagons of each size (in order of size) is the Fibonacci sequence from the second term: 1, 2, 3, 5, 8, 13, 21, .... The number of isosceles triangles of each size (in order of size) is the Fibonacci sequence from the first term: 1, 1, 2, 3, 5, 8, 13, 21, ....^[1]

0.00 (0 votes)