Angle of view

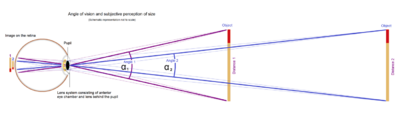
The angle of view is the decisive variable for the visual perception of the size or projection of the size of an object.

Angle of view and perception of size

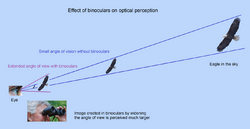
The perceived size of an object depends on the size of the image projected onto the retina. The size of the image depends on the angle of vision. A near and a far object can appear the same size if their edges produce the same angle of vision. With an optical device such as glasses or binoculars, microscope and telescope the angle of vision can be widened so that the object appears larger, which is favourable for the resolving power of the eye (see visual angle).^[1][2]

Angle of view in photography

A camera's angle of view can be measured horizontally, vertically, or diagonally.

In photography, angle of view (AOV)^[3] describes the angular extent of a given scene that is imaged by a camera. It is used interchangeably with the more general term field of view.

It is important to distinguish the angle of view from the angle of coverage, which describes the angle range that a lens can image. Typically the image circle produced by a lens is large enough to cover the film or sensor completely, possibly including some vignetting toward the edge. If the angle of coverage of the lens does not fill the sensor, the image circle will be visible, typically with strong vignetting toward the edge, and the effective angle of view will be limited to the angle of coverage.

In 1916, Northey showed how to calculate the angle of view using ordinary carpenter's tools.^[4] The angle that he labels as the angle of view is the half-angle or "the angle that a straight line would take from the extreme outside of the field of view to the center of the lens;" he notes that manufacturers of lenses use twice this angle.

In this simulation, adjusting the angle of view and distance of the camera while keeping the object in frame results in vastly differing images. At distances approaching infinity, the light rays are nearly parallel to each other, resulting in a "flattened" image. At low distances and high angles of view objects appear "foreshortened".

A camera's angle of view depends not only on the lens, but also on the sensor. Digital sensors are usually smaller than 35 mm film, and this causes the lens to have a narrower angle of view than with 35 mm film, by a constant factor for each sensor (called the crop factor). In everyday digital cameras, the crop factor can range from around 1 (professional digital SLRs), to 1.6 (consumer SLR), to 2 (Micro Four Thirds ILC) to 6 (most compact cameras). So a standard 50 mm lens for 35 mm photography acts like a 50 mm standard "film" lens on a professional digital SLR, but would act closer to an 80 mm lens (1.6 x 50mm) on many mid-market DSLRs, and the 40 degree angle of view of a standard 50 mm lens on a film camera is equivalent to an 80 mm lens on many digital SLRs.

Calculating a camera's angle of view

For lenses projecting rectilinear (non-spatially-distorted) images of distant objects, the effective focal length and the image format dimensions completely define the angle of view. Calculations for lenses producing non-rectilinear images are much more complex and in the end not very useful in most practical applications. (In the case of a lens with distortion, e.g., a fisheye lens, a longer lens with distortion can have a wider angle of view than a shorter lens with low distortion)^[5] Angle of view may be measured horizontally (from the left to right edge of the frame), vertically (from the top to bottom of the frame), or diagonally (from one corner of the frame to its opposite corner).

For a lens projecting a rectilinear image (focused at infinity, see derivation), the angle of view (α) can be calculated from the chosen dimension (d), and effective focal length (f) as follows:^[6] [math]\displaystyle{ \alpha = 2 \arctan \frac {d} {2 f} }[/math]

[math]\displaystyle{ d }[/math] represents the size of the film (or sensor) in the direction measured (see below: sensor effects). For example, for 35 mm film which is 36 mm wide and 24 mm high, [math]\displaystyle{ d = 36\,\mathrm{mm} }[/math] would be used to obtain the horizontal angle of view and [math]\displaystyle{ d = 24\,\mathrm{mm} }[/math] for the vertical angle.

Because this is a trigonometric function, the angle of view does not vary quite linearly with the reciprocal of the focal length. However, except for wide-angle lenses, it is reasonable to approximate [math]\displaystyle{ \alpha \approx \frac{d}{f} }[/math] radians or [math]\displaystyle{ \frac{180d}{\pi f} }[/math] degrees.

The effective focal length is nearly equal to the stated focal length of the lens (F), except in macro photography where the lens-to-object distance is comparable to the focal length. In this case, the magnification factor (m) must be taken into account: [math]\displaystyle{ f = F \cdot ( 1 + m ) }[/math]

(In photography [math]\displaystyle{ m }[/math] is usually defined to be positive, despite the inverted image.) For example, with a magnification ratio of 1:2, we find [math]\displaystyle{ f = 1.5 \cdot F }[/math] and thus the angle of view is reduced by 33% compared to focusing on a distant object with the same lens.

Angle of view can also be determined using FOV tables or paper or software lens calculators.^[7]

Log-log graphs of focal length vs crop factor vs diagonal, horizontal and vertical angles of view for film or sensors of 3:2 and 4:3 aspect ratios. The yellow line shows an example where 18 mm on 3:2 APS-C is equivalent to 27 mm and yields a vertical angle of 48 degrees.

Example

Consider a 50 mm camera with a lens having a focal length of F = 50 mm. The dimensions of the 35 mm image format are 24 mm (vertically) × 36 mm (horizontal), giving a diagonal of about 43.3 mm.

At infinity focus, f = F, the angles of view are:

• horizontally, [math]\displaystyle{ \alpha_h = 2\arctan\frac{h}{2f} = 2\arctan\frac{36}{2 \times 50}\approx 39.6^\circ }[/math]
• vertically, [math]\displaystyle{ \alpha_v = 2\arctan\frac{v}{2f} = 2\arctan\frac{24}{2 \times 50}\approx 27.0^\circ }[/math]
• diagonally, [math]\displaystyle{ \alpha_d = 2\arctan\frac{d}{2f} = 2\arctan\frac{43.3}{2 \times 50}\approx 46.8^\circ }[/math]

Derivation of the angle-of-view formula

Consider a rectilinear lens in a camera used to photograph an object at a distance [math]\displaystyle{ S_1 }[/math], and forming an image that just barely fits in the dimension, [math]\displaystyle{ d }[/math], of the frame (the film or image sensor). Treat the lens as if it were a pinhole at distance [math]\displaystyle{ S_2 }[/math] from the image plane (technically, the center of perspective of a rectilinear lens is at the center of its entrance pupil):^[8]

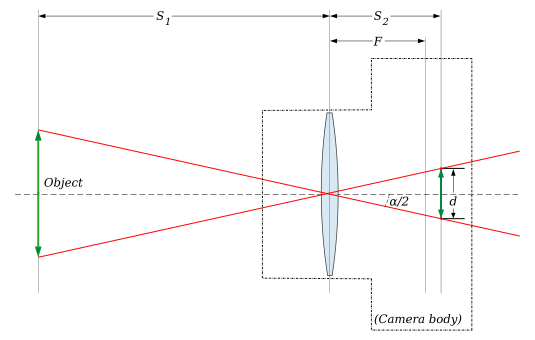
Now [math]\displaystyle{ \alpha/2 }[/math] is the angle between the optical axis of the lens and the ray joining its optical center to the edge of the film. Here [math]\displaystyle{ \alpha }[/math] is defined to be the angle-of-view, since it is the angle enclosing the largest object whose image can fit on the film. We want to find the relationship between:

• the angle [math]\displaystyle{ \alpha }[/math]
• the "opposite" side of the right triangle, [math]\displaystyle{ d/2 }[/math] (half the film-format dimension)
• the "adjacent" side, [math]\displaystyle{ S_2 }[/math] (distance from the lens to the image plane)

Using basic trigonometry, we find: [math]\displaystyle{ \tan ( \alpha / 2 ) = \frac {d/2} {S_2} . }[/math] which we can solve for α, giving: [math]\displaystyle{ \alpha = 2 \arctan \frac {d} {2 S_2} }[/math]

To project a sharp image of distant objects, [math]\displaystyle{ S_2 }[/math] needs to be equal to the focal length, [math]\displaystyle{ F }[/math], which is attained by setting the lens for infinity focus. Then the angle of view is given by:

[math]\displaystyle{ \alpha = 2 \arctan \frac {d} {2 f} }[/math] where [math]\displaystyle{ f = F }[/math].

Note that the angle of view varies slightly when the focus is not at infinity (See breathing (lens)), given by [math]\displaystyle{ S_2 = \frac{S_1 f}{S_1 - f} }[/math] rearranging the lens equation.

Macro photography

For macro photography, we cannot neglect the difference between [math]\displaystyle{ S_2 }[/math] and [math]\displaystyle{ F }[/math]. From the thin lens formula, [math]\displaystyle{ \frac{1}{F} = \frac{1}{S_1} + \frac{1}{S_2}. }[/math]

From the definition of magnification, [math]\displaystyle{ m = S_2/S_1 }[/math], we can substitute [math]\displaystyle{ S_1 }[/math] and with some algebra find: [math]\displaystyle{ S_2 = F\cdot(1+m) }[/math]

Defining [math]\displaystyle{ f=S_2 }[/math] as the "effective focal length", we get the formula presented above: [math]\displaystyle{ \alpha = 2 \arctan \frac {d} {2 f} }[/math] where [math]\displaystyle{ f = F\cdot(1+m) }[/math].

A second effect which comes into play in macro photography is lens asymmetry (an asymmetric lens is a lens where the aperture appears to have different dimensions when viewed from the front and from the back). The lens asymmetry causes an offset between the nodal plane and pupil positions. The effect can be quantified using the ratio (P) between apparent exit pupil diameter and entrance pupil diameter. The full formula for angle of view now becomes:^[9] [math]\displaystyle{ \alpha = 2 \arctan \frac {d} {2 F\cdot ( 1 + m/P )} }[/math]

Measuring a camera's field of view

Schematic of collimator-based optical apparatus used in measuring the FOV of a camera.

In the optical instrumentation industry the term field of view (FOV) is most often used, though the measurements are still expressed as angles.^[10] Optical tests are commonly used for measuring the FOV of UV, visible, and infrared (wavelengths about 0.1–20 μm in the electromagnetic spectrum) sensors and cameras.

The purpose of this test is to measure the horizontal and vertical FOV of a lens and sensor used in an imaging system, when the lens focal length or sensor size is not known (that is, when the calculation above is not immediately applicable). Although this is one typical method that the optics industry uses to measure the FOV, there exist many other possible methods.

UV/visible light from an integrating sphere (and/or other source such as a black body) is focused onto a square test target at the focal plane of a collimator (the mirrors in the diagram), such that a virtual image of the test target will be seen infinitely far away by the camera under test. The camera under test senses a real image of the virtual image of the target, and the sensed image is displayed on a monitor.^[11]

Monitor display of sensed image from the camera under test

The sensed image, which includes the target, is displayed on a monitor, where it can be measured. Dimensions of the full image display and of the portion of the image that is the target are determined by inspection (measurements are typically in pixels, but can just as well be inches or cm).

• [math]\displaystyle{ D }[/math] = dimension of full image
• [math]\displaystyle{ d }[/math] = dimension of image of target

The collimator's distant virtual image of the target subtends a certain angle, referred to as the angular extent of the target, that depends on the collimator focal length and the target size. Assuming the sensed image includes the whole target, the angle seen by the camera, its FOV, is this angular extent of the target times the ratio of full image size to target image size.^[12]

The target's angular extent is: [math]\displaystyle{ \alpha = 2 \arctan \frac {L} {2 f_c} }[/math] where [math]\displaystyle{ L }[/math] is the dimension of the target and [math]\displaystyle{ f_c }[/math] is the focal length of collimator.

The total field of view is then approximately: [math]\displaystyle{ \mathrm{FOV} = \alpha \frac{D}{d} }[/math] or more precisely, if the imaging system is rectilinear: [math]\displaystyle{ \mathrm{FOV} = 2 \arctan \frac {LD} {2 f_c d} }[/math]

This calculation could be a horizontal or a vertical FOV, depending on how the target and image are measured.

Lens types and effects

Focal length

How focal length affects perspective: Varying focal lengths at identical field size achieved by different camera-subject distances. Notice that the shorter the focal length and the larger the angle of view, perspective distortion and size differences increase.

Lenses are often referred to by terms that express their angle of view:

• Fisheye lenses, typical focal lengths are between 8 mm and 10 mm for circular images, and 15–16 mm for full-frame images. Up to 180° and beyond.
  • A circular fisheye lens (as opposed to a full-frame fisheye) is an example of a lens where the angle of coverage is less than the angle of view. The image projected onto the film is circular because the diameter of the image projected is narrower than that needed to cover the widest portion of the film.
• Ultra wide angle lens is a rectilinear which is less than 24 mm of focal length in 35 mm film format, here 14 mm gives 114° and 24 mm gives 84° .
• Wide-angle lenses (24–35 mm in 35 mm film format) cover between 84° and 64°
• Normal, or Standard lenses (36–60 mm in 35 mm film format) cover between 62° and 40°
• Long focus lenses (any lens with a focal length greater than the diagonal of the film or sensor used)^[13] generally have an angle of view of 35° or less.^[14] Since photographers usually only encounter the telephoto lens sub-type,^[15] they are referred to in common photographic parlance as:
• "Medium telephoto", a focal length of 85 mm to 250 mm in 35 mm film format covering between 30° and 10°^[16]
• "Super telephoto" (over 300 mm in 35 mm film format) generally cover between 8° through less than 1°^[16]

Zoom lenses are a special case wherein the focal length, and hence angle of view, of the lens can be altered mechanically without removing the lens from the camera.

Characteristics

For a given camera–subject distance, longer lenses magnify the subject more. For a given subject magnification (and thus different camera–subject distances), longer lenses appear to compress distance; wider lenses appear to expand the distance between objects.

Another result of using a wide angle lens is a greater apparent perspective distortion when the camera is not aligned perpendicularly to the subject: parallel lines converge at the same rate as with a normal lens, but converge more due to the wider total field. For example, buildings appear to be falling backwards much more severely when the camera is pointed upward from ground level than they would if photographed with a normal lens at the same distance from the subject, because more of the subject building is visible in the wide-angle shot.

Because different lenses generally require a different camera–subject distance to preserve the size of a subject, changing the angle of view can indirectly distort perspective, changing the apparent relative size of the subject and foreground.

If the subject image size remains the same, then at any given aperture all lenses, wide angle and long lenses, will give the same depth of field.^[17]

Examples

An example of how lens choice affects angle of view.

28 mm lens, 65.5° × 46.4°	50 mm lens, 39.6° × 27.0°
70 mm lens, 28.9° × 19.5°	210 mm lens, 9.8° × 6.5°

Common lens angles of view

This table shows the diagonal, horizontal, and vertical angles of view, in degrees, for lenses producing rectilinear images, when used with 36 mm × 24 mm format (that is, 135 film or full-frame 35 mm digital using width 36 mm, height 24 mm, and diagonal 43.3 mm for d in the formula above).^[18] Digital compact cameras sometimes state the focal lengths of their lenses in 35 mm equivalents, which can be used in this table.

For comparison, the human visual system perceives an angle of view of about 140° by 80°.^[19]

Five images using 24, 28, 35, 50 and 72 mm equivalent zoom lengths, portrait format, to illustrate angles of view^[20]

Five images using 24, 28, 35, 50 and 72 mm equivalent step zoom function, to illustrate angles of view

Sensor size effects ("crop factor")

Main page: Physics:Crop factor

As noted above, a camera's angle level of view depends not only on the lens, but also on the sensor used. Digital sensors are usually smaller than 35 mm film, causing the lens to usually behave as a longer focal length lens would behave, and have a narrower angle of view than with 35 mm film, by a constant factor for each sensor (called the crop factor). In everyday digital cameras, the crop factor can range from around 1 (professional digital SLRs), to 1.6 (mid-market SLRs), to around 3 to 6 for compact cameras. So a standard 50 mm lens for 35 mm photography acts like a 50 mm standard "film" lens even on a professional digital SLR, but would act closer to a 75mm (1.5×50 mm Nikon) or 80mm lens (1.6×50 mm Canon) on many mid-market DSLRs, and the 40 degree angle of view of a standard 50mm lens on a film camera is equivalent to a 28–35 mm lens on many digital SLRs.

The table below shows the horizontal, vertical and diagonal angles of view, in degrees, when used with 22.2 mm × 14.8 mm format (that is Canon's DSLR APS-C frame size) and a diagonal of 26.7 mm.

Cinematography and video gaming

Modifying the angle of view over time (known as zooming), is a frequently used cinematic technique, often combined with camera movement to produce a "dolly zoom" effect, made famous by the film Vertigo. Using a wide angle of view can exaggerate the camera's perceived speed, and is a common technique in tracking shots, phantom rides, and racing video games. See also Field of view in video games.

See also

• 35 mm equivalent focal length
• Camera angle
• Camera coverage
• Camera operator
• Cinematic techniques
• Field of view
• Filmmaking
• Multiple-camera setup
• Single-camera setup
• Video production
• Image sensor format
• Crop factor
• Ultrawide formats

Notes and references

External links

• Simple Explanation of Angle of View and Focal Length
• Angle of View on digital SLR cameras with reduced sensor size
• Focal Length and Angle of View

0.00 (0 votes)