Arithmetic number

Demonstration, with Cuisenaire rods, of the arithmetic nature of the number 6

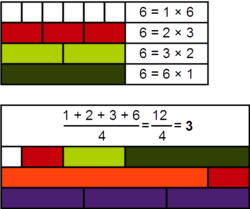
In number theory, an arithmetic number is an integer for which the average of its positive divisors is also an integer. For instance, 6 is an arithmetic number because the average of its divisors is

[math]\displaystyle{ \frac{1+2+3+6}{4}=3, }[/math]

which is also an integer. However, 2 is not an arithmetic number because its only divisors are 1 and 2, and their average 3/2 is not an integer.

The first numbers in the sequence of arithmetic numbers are

1, 3, 5, 6, 7, 11, 13, 14, 15, 17, 19, 20, 21, 22, 23, 27, 29, 30, 31, 33, 35, 37, 38, 39, 41, 42, 43, 44, 45, 46, 47, 49, ... (sequence A003601 in the OEIS).

Density

It is known that the natural density of such numbers is 1:^[1] indeed, the proportion of numbers less than X which are not arithmetic is asymptotically^[2]

[math]\displaystyle{ \exp\left( { -c \sqrt{\log\log X} } \,\right) }[/math]

where c = 2√log 2 + o(1).

A number N is arithmetic if the number of divisors d(N ) divides the sum of divisors σ(N ). It is known that the density of integers N obeying the stronger condition that d(N )² divides σ(N ) is 1/2.^[1][2]

Notes

References

• Guy, Richard K. (2004). Unsolved problems in number theory (3rd ed.). Springer-Verlag. B2. ISBN 978-0-387-20860-2. 

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Arithmetic number. Read more