Associative magic square
From HandWiki - Reading time: 2 min
.jpg)
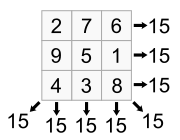
An associative magic square is a magic square for which each pair of numbers symmetrically opposite to the center sum up to the same value. For an n × n square, filled with the numbers from 1 to n2, this common sum must equal n2 + 1. These squares are also called associated magic squares, regular magic squares, regmagic squares, or symmetric magic squares.[1][2][3]
Examples
For instance, the Lo Shu Square – the unique 3 × 3 magic square – is associative, because each pair of opposite points form a line of the square together with the center point, so the sum of the two opposite points equals the sum of a line minus the value of the center point regardless of which two opposite points are chosen.[4] The 4 × 4 magic square from Albrecht Dürer's 1514 engraving Melencolia I – also found in a 1765 letter of Benjamin Franklin – is also associative, with each pair of opposite numbers summing to 17.[5]
Existence and enumeration
The numbers of possible associative n × n magic squares for n = 3,4,5,..., counting two squares as the same whenever they differ only by a rotation or reflection, are:
The number zero for n = 6 is an example of a more general phenomenon: associative magic squares do not exist for values of n that are singly even (equal to 2 modulo 4).[3] Every associative magic square of even order forms a singular matrix, but associative magic squares of odd order can be singular or nonsingular.[4]
References
- ↑ Frierson, L. S. (1917), "Notes on pandiagonal and associated magic squares", in Andrews, W. S., Magic Squares and Cubes (2nd ed.), Open Court, pp. 229–244, https://archive.org/details/MagicSquaresCubesAndrewsEdited/page/n237/mode/2up
- ↑ Bell, Jordan; Stevens, Brett (2007), "Constructing orthogonal pandiagonal Latin squares and panmagic squares from modular [math]\displaystyle{ n }[/math]-queens solutions", Journal of Combinatorial Designs 15 (3): 221–234, doi:10.1002/jcd.20143
- ↑ 3.0 3.1 Nordgren, Ronald P. (2012), "On properties of special magic square matrices", Linear Algebra and Its Applications 437 (8): 2009–2025, doi:10.1016/j.laa.2012.05.031
- ↑ 4.0 4.1 Lee, Michael Z.; Love, Elizabeth; Narayan, Sivaram K.; Wascher, Elizabeth; Webster, Jordan D. (2012), "On nonsingular regular magic squares of odd order", Linear Algebra and Its Applications 437 (6): 1346–1355, doi:10.1016/j.laa.2012.04.004
- ↑ Pasles, Paul C. (2001), "The lost squares of Dr. Franklin: Ben Franklin's missing squares and the secret of the magic circle", American Mathematical Monthly 108 (6): 489–511, doi:10.1080/00029890.2001.11919777
External links
- Weisstein, Eric W.. "Associative Magic Square". http://mathworld.wolfram.com/AssociativeMagicSquare.html.
| Types |  | |
|---|---|---|
| Related shapes | ||
| Higher dimensional shapes | ||
| Related concepts | ||
 |  |
EncycloReader
is supported by the 
KSF