Cosmic microwave background spectral distortions

CMB spectral distortions are tiny departures of the average cosmic microwave background (CMB) frequency spectrum from the predictions given by a perfect black body. They can be produced by a number of standard and non-standard processes occurring at the early stages of cosmic history, and therefore allow us to probe the standard picture of cosmology. Importantly, the CMB frequency spectrum and its distortions should not be confused with the CMB anisotropy power spectrum, which relates to spatial fluctuations of the CMB temperature in different directions of the sky.^[1]

Spectral distortions at different cosmological epochs. At very early times, with redshift [math]\displaystyle{ z\gt 2\times10^6 }[/math], any injection of energy emerges as a temperature shift in the black body. As the age of the Universe increases, the processes that lead to thermalization of CMB distortions to a blackbody become less efficient (bremsstrahlung and double Compton scattering when [math]\displaystyle{ z\lt 10^6 }[/math], Compton scattering when [math]\displaystyle{ z\lt 10^4 }[/math]). The spectral distortions also interplay with distinguished epochs of cosmic history such as reionization, recombination and Big Bang nucleosynthesis as shown. Specifically, during the recombination epoch ([math]\displaystyle{ \sim300,000 }[/math] years after the Big Bang), the cosmological recombination lines are imprinted on the CMB as a result of non-equilibrium atomic processes during that era ^[2]

Overview

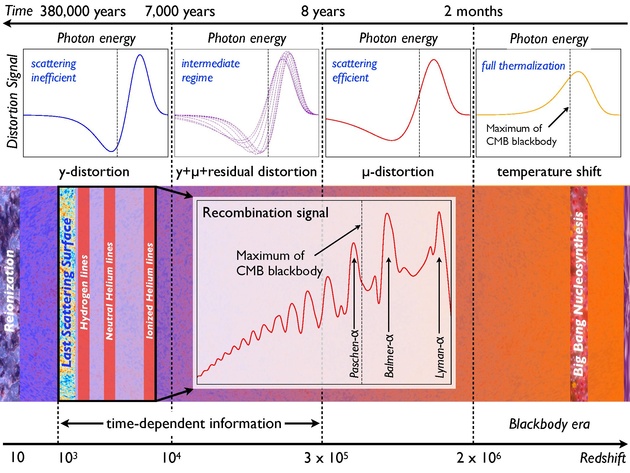
The energy spectrum of the CMB is extremely close to that of a perfect blackbody with a temperature of [math]\displaystyle{ 2.7255 K }[/math].^[3][4] This is expected because in the early Universe matter and radiation are in thermal equilibrium. However, at redshifts [math]\displaystyle{ z\lt 2\times10^6 }[/math], several mechanisms, both standard and non-standard, can modify the CMB spectrum and introduce departures from a blackbody spectrum. These departures are commonly referred to as CMB spectral distortions and mostly concern the average CMB spectrum across the full sky (i.e., the CMB monopole spectrum).

Spectral distortions are created by processes that drive matter and radiation out of equilibrium. One important scenario relates to spectral distortions from early energy injection, for instance, by decaying particles, primordial black hole evaporation or the dissipation of acoustic waves set up by inflation. In this process, the baryons heat up and transfer some of their excess energy to the ambient CMB photon bath via Compton scattering. Depending on the moment of injection, this causes a distortion, which can be characterized using so-called [math]\displaystyle{ \mu }[/math]- and [math]\displaystyle{ y }[/math]-type distortion spectra. The dimensionless [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ y }[/math]-parameters are a measure for the total amount of energy that was injected into the CMB. CMB spectral distortions therefore provide a powerful probe of early-universe physics and even deliver crude estimates for the epoch at which the injection occurred.^[5]

The current best observational limits set in the 1990s by COBE-satellite/FIRAS-instrument (COBE/FIRAS) are [math]\displaystyle{ |\mu|\lt 9\times 10^{-5} }[/math] and [math]\displaystyle{ |y|\lt 1.5\times 10^{-5} }[/math] at 95% confidence level. Within [math]\displaystyle{ \Lambda }[/math]CDM we expect [math]\displaystyle{ \mu\sim2\times 10^{-8} }[/math] and [math]\displaystyle{ y\sim{\rm few}\times10^{-6} }[/math], signals that have come into reach of current-day technology (see § Experimental and observational challenges). Richer distortion signals, going beyond the classical [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ y }[/math] distortions, can be created by photon injection processes, relativistic electron distributions and during the gradual transition between the [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ y }[/math]-distortion eras. The cosmological recombination radiation (CRR) is a prime example within [math]\displaystyle{ \Lambda }[/math]CDM that is created by photon injection from the recombining hydrogen and helium plasma around redshifts of [math]\displaystyle{ z\sim10^3-10^4 }[/math].

History

The first considerations of spectral distortions to the CMB go back to the early days of CMB cosmology starting with the seminal papers of Yakov B. Zeldovich and Rashid Sunyaev in 1969 and 1970. These works appeared just a few years after the first detection of the CMB by Arno Allan Penzias and Robert Woodrow Wilson and its interpretation as the echo of the Big Bang by Robert H. Dicke and his team in 1965.^[6][7] These findings constitute one of the most important pillars of Big Bang cosmology, which predicts the blackbody nature of the CMB. However, as shown by Zeldovich and Sunyaev, energy exchange with moving electrons can cause spectral distortions.

The pioneering analytical studies of Zeldovich and Sunyaev were later complemented by the numerical investigations of Illarionov and Sunyaev in the 1970s. These treated the thermalization problem including Compton scattering and the Bremsstrahlung process for a single release of energy. In 1982, the importance of double Compton emission as a source of photons at high redshifts was recognized by Danese and de Zotti. Modern considerations of CMB spectral distortions started with the works of Burigana, Danese and de Zotti and Hu, Silk and Scott in the early 1990s.

After COBE/FIRAS provided stringent limits on the CMB spectrum, essentially ruling out distortions at the level [math]\displaystyle{ \tfrac{\Delta I}{I} \sim 10^{-5}-10^{-4} }[/math], the interest in CMB spectral distortions decreased. In 2011, PIXIE^[8] was proposed to NASA as a mid-Ex satellite mission, providing first strong motivation to revisit the theory of spectral distortions. Although no successor of COBE/FIRAS has been funded so far, this led to a renaissance of CMB spectral distortions with numerous theoretical studies and the design of novel experimental concepts ^[9]

The spectral distortion in the cosmic microwave background (CMB) looks different depending on the moment in the universe's history where this black body was modified. At very early times where [math]\displaystyle{ z\gt 10^6 }[/math], any injection of energy emerges as a temperature shift in the black body. If the energy injection is later (still very early in the Universe's history), we see the shape of the [math]\displaystyle{ \mu }[/math]- distortion, whereas we can see a sharper fluctuation at later times, associated with [math]\displaystyle{ y }[/math]-distortion. Here some energy is injected into the CMB at time defined by the redshift [math]\displaystyle{ z_h }[/math] with the resultant distortion being plotted.

Thermalisation physics

In the cosmological 'thermalization problem', three main eras are distinguished: the thermalization or temperature-era, the [math]\displaystyle{ \mu }[/math]-era and the [math]\displaystyle{ y }[/math]-era, each with slightly different physical conditions due to the change in the density and temperature of particles caused by the Hubble expansion.

Thermalization era

In the very early stages of cosmic history (up until a few months after the Big Bang), photons and baryons^[10] are efficiently coupled by scattering processes and, therefore, are in full thermodynamic equilibrium. Energy that is injected into the medium is rapidly redistributed among the photons, mainly by Compton scattering, while the photon number density is adjusted by photon non-conserving processes, such as double Compton and thermal Bremsstrahlung. This allows the photon field to quickly relax back to a Planckian distribution, even if for a very short phase a spectral distortion appears. Observations today cannot tell the difference in this case, as there is no independent cosmological prediction for the CMB monopole temperature.^[11] This regime is frequently referred to as the thermalization or temperature era and ends at redshift [math]\displaystyle{ z\sim2\times10^{6} }[/math].

μ-distortion era

At redshifts between [math]\displaystyle{ 5\times10^4 }[/math] and [math]\displaystyle{ 2\times10^6 }[/math], efficient energy exchange through Compton scattering continues to establish kinetic equilibrium between matter and radiation, but photon number changing processes stop being efficient. Since the photon number density is conserved but the energy density is modified, photons gain an effective non-zero chemical potential, acquiring a Bose-Einstein distribution. This distinct type of distortion is called [math]\displaystyle{ \mu }[/math]-distortion after the chemical potential known from standard thermodynamics.^[12] The value for the chemical potential can be estimated by combining the photon energy density and number density constraints from before and after the energy injection. This yields the well-known expression,^[13]

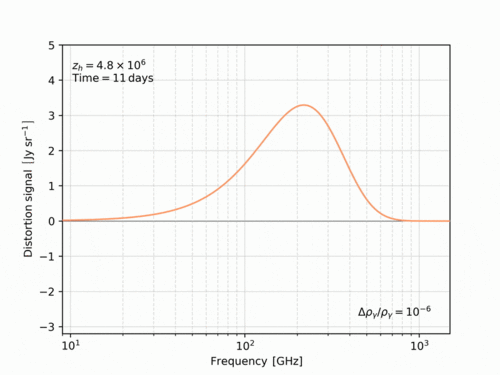
[math]\displaystyle{ \mu \sim 1.4\; \frac{\Delta \rho}{\rho}, }[/math] where [math]\displaystyle{ \tfrac{\Delta \rho}{\rho} }[/math] determines the total energy that is injected into the CMB photon field. With respect to the equilibrium blackbody spectrum, the [math]\displaystyle{ \mu }[/math]-distortion is characterized by a deficit of photons at low frequencies and an increment at high frequencies. The distortion changes sign at a frequency of [math]\displaystyle{ \nu\sim130 {\rm GHz} }[/math], allowing us to distinguish it observationally from the [math]\displaystyle{ y }[/math]-type distortion.

[math]\displaystyle{ \mu }[/math]-distortion signals can be created by decaying particles, evaporating primordial black holes, primordial magnetic fields and other non-standard physics examples. Within [math]\displaystyle{ \Lambda }[/math]CDM cosmology, the adiabatic cooling of matter and dissipation of acoustic waves set up by inflation cause a [math]\displaystyle{ \mu }[/math]-distortion with [math]\displaystyle{ \mu\sim2\times10^{-8} }[/math]. This signal can be used as a powerful test for inflation, as it is sensitive to the amplitude of density fluctuations at scales corresponding to physical scales of [math]\displaystyle{ \lambda\sim0.6 \,{\rm kpc} }[/math] (i.e., dwarf galaxies). By combining COBE’s measurements of the large-scale CMB anisotropies with the [math]\displaystyle{ \mu }[/math]-distortion constraint, the first limits on the small-scale power spectrum could be obtained well-before direct measurements became possible ^[14]

y-distortion era

At redshifts [math]\displaystyle{ z\lesssim5\times10^4 }[/math], also Compton scattering becomes inefficient. The plasma has a temperature of [math]\displaystyle{ T\lt 10^5 {\rm K} }[/math], such that CMB photons are boosted via non-relativistic Compton scattering, giving rise to a [math]\displaystyle{ y }[/math]-distortion. Again, by considering the total energetics of the problem and using photon number conservation, one can obtain the estimate^[15]

[math]\displaystyle{ y \sim \frac{1}{4}\; \frac{\Delta \rho}{\rho}. }[/math] The name for the [math]\displaystyle{ y }[/math]-distortion simply stems from the choice of dimensionless variables in the seminal paper of Zeldovich and Sunyaev, 1969.^[15] There, the energy injection caused by the hot electrons residing inside clusters of galaxies was considered and the associated effect is more commonly referred to as the thermal Sunyaev-Zeldovich (SZ) effect. Like for the [math]\displaystyle{ \mu }[/math]-distortion, in principle many non-standard physics examples can cause [math]\displaystyle{ y }[/math]-type distortions. However, the largest contribution to the all-sky [math]\displaystyle{ y }[/math]-distortion stems from the cumulative cluster SZ signal, which provides a way to constrain the amount of hot gas in the Universe. While at [math]\displaystyle{ z\lt 10^4 }[/math], the cosmic plasma on average has a low temperature, electrons inside galaxy clusters can reach temperatures of a few keV. In this case, the scattering electrons can have speeds of [math]\displaystyle{ v\sim0.1 c }[/math], such that relativistic corrections to the Compton process become relevant. These relativistic corrections carry information of electron temperatures which can be used as a measure for the cluster energetics.^[16]

Beyond μ and y distortions

The classical studies mainly considered energy release (i.e., heating) as a source of distortions. However, recent work has shown that richer signals can be created by direct photon injection and non-thermal electron populations, both processes that appear in connection with decaying or annihilating particles. Similarly, it was demonstrated that the transition between the [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ y }[/math]-eras is more gradual and that the distortion shape is not simply given by a sum of [math]\displaystyle{ \mu }[/math]- and [math]\displaystyle{ y }[/math]. All these effects could allow us to differentiate observationally between a wide range of scenarios, as additional time-dependent information can be extracted.

Cosmological recombination radiation (CRR)

About 280,000 years after the Big Bang, electrons and protons became bound into electrically neutral atoms as the Universe expanded. In cosmology, this is known as recombination and preludes the decoupling of the CMB photons from matter before they free stream throughout the Universe around 380,000 years after the Big Bang. Within the energy levels of hydrogen and helium atoms, various interactions take place, both collisional and radiative. The line emission arising from these processes is injected into the CMB, showing as small distortions to the CMB blackbody commonly referred to as the cosmological recombination radiation (CRR). The specific spectral shape of this distortion is directly related to the redshift at which this emission takes place, freezing the distortion in time over the microwave frequency bands. Since the distortion signal arises from the hydrogen and two helium recombination eras, this gives us a unique probe of the pre-recombination Universe that allows us to peek behind the last scattering surface that we observe using the CMB anisotropies.^[2] It gives us a unique way to constrain the primordial amount of helium in the early Universe, before recombination, and measure the early expansion rate.

Experimental and observational challenges

The expected Lambda-CDM (LCDM) distortion signals are small – The largest distortion, arising from the cumulative flux of all hot gas in the Universe, has an amplitude that is about one order of magnitude below the limits of COBE/FIRAS. While this is considered to be an ‘easy’ target, the cosmological recombination radiation (CRR), as the smallest expected signal, has an amplitude that is another factor of [math]\displaystyle{ 10^3 }[/math] smaller. All LCDM distortions are furthermore obscured by large Galactic and extragalactic foreground emissions (e.g., dust, synchrotron and free-free emission, cosmic infrared background), and for observations from the ground or balloons, atmospheric emission poses another hurdle to overcome.

A detection of the LCDM distortions therefore requires novel experimental approaches that provide unprecedented sensitivity, spectral coverage, control of systematics and the capabilities to accurately remove foregrounds. Building on the design of FIRAS and experience with ARCADE, this has led to several spectrometer concepts to observe from space (PIXIE, PRISM, PRISTINE, SuperPIXIE and Voyage2050),^[8][2] balloon (BISOU) and the ground (APSERa and Cosmo at Dome-C, TMS at Teide Observatory). These are all designed to reach important milestones towards a detection of CMB distortions. As an ultimate frontier, a full characterization and exploitation of the cosmological recombination signal could be achieved by using a coordinated international experimental campaign, potentially including an observatory on the moon ^[17]

In June 2021, the European Space Agency unveiled its plans for the future L-class missions as part of Voyage 2050 with a chance for `high precision spectroscopy` for the new early universe part of their strategy, opening the door for spectral distortions telescopes for the future.^[18]

See also

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Cosmic microwave background spectral distortions. Read more