Extinction

An extreme example of visible light extinction, caused by a dark nebula

In astronomy, extinction is the absorption and scattering of electromagnetic radiation by dust and gas between an emitting astronomical object and the observer. Interstellar extinction was first documented as such in 1930 by Robert Julius Trumpler.^[1][2] However, its effects had been noted in 1847 by Friedrich Georg Wilhelm von Struve,^[3] and its effect on the colors of stars had been observed by a number of individuals who did not connect it with the general presence of galactic dust. For stars lying near the plane of the Milky Way which are within a few thousand parsecs of the Earth, extinction in the visual band of frequencies (photometric system) is roughly 1.8 magnitudes per kiloparsec.^[4]

For Earth-bound observers, extinction arises both from the interstellar medium (ISM) and the Earth's atmosphere; it may also arise from circumstellar dust around an observed object. Strong extinction in Earth's atmosphere of some wavelength regions (such as X-ray, ultraviolet, and infrared) is overcome by the use of space-based observatories. Since blue light is much more strongly attenuated than red light, extinction causes objects to appear redder than expected, a phenomenon referred to as interstellar reddening.^[5]

Interstellar reddening

In astronomy, interstellar reddening is a phenomenon associated with interstellar extinction where the spectrum of electromagnetic radiation from a radiation source changes characteristics from that which the object originally emitted. Reddening occurs due to the light scattering off dust and other matter in the interstellar medium. Interstellar reddening is a different phenomenon from redshift, which is the proportional frequency shifts of spectra without distortion. Reddening preferentially removes shorter wavelength photons from a radiated spectrum while leaving behind the longer wavelength photons (in the optical, light that is redder), leaving the spectroscopic lines unchanged.

In most photometric systems filters (passbands) are used from which readings of magnitude of light may take account of latitude and humidity among terrestrial factors. Interstellar reddening equates to the "color excess", defined as the difference between an object's observed color index and its intrinsic color index (sometimes referred to as its normal color index). The latter is the theoretical value which it would have if unaffected by extinction. In the first system, the UBV photometric system devised in the 1950s and its most closely related successors, the object's color excess [math]\displaystyle{ E_{B-V} }[/math] is related to the object's B−V color (calibrated blue minus calibrated visible) by:

For an A0-type main sequence star (these have median wavelength and heat among the main sequence) the color indices are calibrated at 0 based on an intrinsic reading of such a star (± exactly 0.02 depending on which spectral point, i.e. precise passband within the abbreviated color name is in question, see color index). At least two and up to five measured passbands in magnitude are then compared by subtraction: U, B, V, I, or R during which the color excess from extinction is calculated and deducted. The name of the four sub-indices (R minus I etc.) and order of the subtraction of recalibrated magnitudes is from right to immediate left within this sequence.

General characteristics

Interstellar reddening occurs because interstellar dust absorbs and scatters blue light waves more than red light waves, making stars appear redder than they are. This is similar to the effect seen when dust particles in the atmosphere of Earth contribute to red sunsets (see: Sunset).^[6]

Broadly speaking, interstellar extinction is strongest at short wavelengths, generally observed by using techniques from spectroscopy. Extinction results in a change in the shape of an observed spectrum. Superimposed on this general shape are absorption features (wavelength bands where the intensity is lowered) that have a variety of origins and can give clues as to the chemical composition of the interstellar material, e.g. dust grains. Known absorption features include the 2175 Å bump, the diffuse interstellar bands, the 3.1 μm water ice feature, and the 10 and 18 μm silicate features.

In the solar neighborhood, the rate of interstellar extinction in the Johnson–Cousins V-band (visual filter) averaged at a wavelength of 540 nm is usually taken to be 0.7–1.0 mag/kpc−simply an average due to the clumpiness of interstellar dust.^[7][8][9] In general, however, this means that a star will have its brightness reduced by about a factor of 2 in the V-band viewed from a good night sky vantage point on earth for every kiloparsec (3,260 light years) it is farther away from us.

The amount of extinction can be significantly higher than this in specific directions. For example, some regions of the Galactic Center are awash with obvious intervening dark dust from our spiral arm (and perhaps others) and themselves in a bulge of dense matter, causing as much as more than 30 magnitudes of extinction in the optical, meaning that less than 1 optical photon in 10¹² passes through.^[10] This results in the so-called zone of avoidance, where our view of the extra-galactic sky is severely hampered, and background galaxies, such as Dwingeloo 1, were only discovered recently through observations in radio and infrared.

The general shape of the ultraviolet through near-infrared (0.125 to 3.5 μm) extinction curve (plotting extinction in magnitude against wavelength, often inverted) looking from our vantage point at other objects in the Milky Way, is fairly well characterized by the stand-alone parameter of relative visibility (of such visible light) R(V) (which is different along different lines of sight),^[11][12] but there are known deviations from this characterization.^[13] Extending the extinction law into the mid-infrared wavelength range is difficult due to the lack of suitable targets and various contributions by absorption features.^[14]

R(V) compares aggregate and particular extinctions. It is A(V)/E(B−V). Restated, it is the total extinction, A(V) divided by the selective total extinction (A(B)−A(V)) of those two wavelengths (bands). A(B) and A(V) are the total extinction at the B and V filter bands. Another measure used in the literature is the absolute extinction A(λ)/A(V) at wavelength λ, comparing the total extinction at that wavelength to that at the V band.

R(V) is known to be correlated with the average size of the dust grains causing the extinction. For the Milky Way Galaxy, the typical value for R(V) is 3.1,^[15] but is found to vary considerably across different lines of sight.^[16] As a result, when computing cosmic distances it can be advantageous to move to star data from the near-infrared (of which the filter or passband Ks is quite standard) where the variations and amount of extinction are significantly less, and similar ratios as to R(Ks):^[17] 0.49±0.02 and 0.528±0.015 were found respectively by independent groups.^[16][18] Those two more modern findings differ substantially relative to the commonly referenced historical value ≈0.7.^[11]

The relationship between the total extinction, A(V) (measured in magnitudes), and the column density of neutral hydrogen atoms column, N_H (usually measured in cm⁻²), shows how the gas and dust in the interstellar medium are related. From studies using ultraviolet spectroscopy of reddened stars and X-ray scattering halos in the Milky Way, Predehl and Schmitt^[19] found the relationship between N_H and A(V) to be approximately:

[math]\displaystyle{ \frac{N_H}{A(V)} \approx 1.8 \times 10^{21}~\mbox{atoms}~\mbox{cm}^{-2}~\mbox{mag}^{-1} }[/math]

(see also:^[20][21][22]).

Astronomers have determined the three-dimensional distribution of extinction in the "solar circle" (our region of our galaxy), using visible and near-infrared stellar observations and a model of distribution of stars.^[23][24] The dust causing extinction mainly lies along the spiral arms, as observed in other spiral galaxies.

Measuring extinction towards an object

To measure the extinction curve for a star, the star's spectrum is compared to the observed spectrum of a similar star known not to be affected by extinction (unreddened).^[25] It is also possible to use a theoretical spectrum instead of the observed spectrum for the comparison, but this is less common. In the case of emission nebulae, it is common to look at the ratio of two emission lines which should not be affected by the temperature and density in the nebula. For example, the ratio of hydrogen alpha to hydrogen beta emission is always around 2.85 under a wide range of conditions prevailing in nebulae. A ratio other than 2.85 must therefore be due to extinction, and the amount of extinction can thus be calculated.

The 2175-angstrom feature

One prominent feature in measured extinction curves of many objects within the Milky Way is a broad 'bump' at about 2175 Å, well into the ultraviolet region of the electromagnetic spectrum. This feature was first observed in the 1960s,^[26][27] but its origin is still not well understood. Several models have been presented to account for this bump which include graphitic grains with a mixture of PAH molecules. Investigations of interstellar grains embedded in interplanetary dust particles (IDP) observed this feature and identified the carrier with organic carbon and amorphous silicates present in the grains.^[28]

Extinction curves of other galaxies

Plot showing the average extinction curves for the MW, LMC2, LMC, and SMC Bar.^[29] The curves are plotted versus 1/wavelength to emphasize the UV.

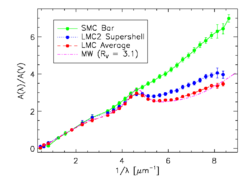
The form of the standard extinction curve depends on the composition of the ISM, which varies from galaxy to galaxy. In the Local Group, the best-determined extinction curves are those of the Milky Way, the Small Magellanic Cloud (SMC) and the Large Magellanic Cloud (LMC).

In the LMC, there is significant variation in the characteristics of the ultraviolet extinction with a weaker 2175 Å bump and stronger far-UV extinction in the region associated with the LMC2 supershell (near the 30 Doradus starbursting region) than seen elsewhere in the LMC and in the Milky Way.^[30][31] In the SMC, more extreme variation is seen with no 2175 Å bump and very strong far-UV extinction in the star forming Bar and fairly normal ultraviolet extinction seen in the more quiescent Wing.^[32][33][34]

This gives clues as to the composition of the ISM in the various galaxies. Previously, the different average extinction curves in the Milky Way, LMC, and SMC were thought to be the result of the different metallicities of the three galaxies: the LMC's metallicity is about 40% of that of the Milky Way, while the SMC's is about 10%. Finding extinction curves in both the LMC and SMC which are similar to those found in the Milky Way^[29] and finding extinction curves in the Milky Way that look more like those found in the LMC2 supershell of the LMC^[35] and in the SMC Bar^[36] has given rise to a new interpretation. The variations in the curves seen in the Magellanic Clouds and Milky Way may instead be caused by processing of the dust grains by nearby star formation. This interpretation is supported by work in starburst galaxies (which are undergoing intense star formation episodes) which shows that their dust lacks the 2175 Å bump.^[37][38]

Atmospheric extinction

Atmospheric extinction gives the rising or setting Sun an orange hue and varies with location and altitude. Astronomical observatories generally are able to characterise the local extinction curve very accurately, to allow observations to be corrected for the effect. Nevertheless, the atmosphere is completely opaque to many wavelengths requiring the use of satellites to make observations.

This extinction has three main components: Rayleigh scattering by air molecules, scattering by particulates, and molecular absorption. Molecular absorption is often referred to as telluric absorption, as it is caused by the Earth (telluric is a synonym for terrestrial). The most important sources of telluric absorption are molecular oxygen and ozone, which strongly absorb radiation near ultraviolet, and water, which strongly absorbs infrared.

The amount of such extinction is lowest at the observer's zenith and highest near the horizon. A given star, preferably at solar opposition, reaches its greatest celestial altitude and optimal time for observation when the star is near the local meridian around solar midnight and if the star has a favorable declination (i.e., similar to the observer's latitude); thus, the seasonal time due to axial tilt is key. Extinction is approximated by multiplying the standard atmospheric extinction curve (plotted against each wavelength) by the mean air mass calculated over the duration of the observation. A dry atmosphere reduces infrared extinction significantly.

References

Further reading

• Binney, J.; Merrifield, M. (1998). Galactic Astronomy. Princeton: Princeton University Press. ISBN 978-0-691-00402-0. 
• Howarth, I. D. (1983). "LMC and galactic extinction". Monthly Notices of the Royal Astronomical Society 203 (2): 301–304. doi:10.1093/mnras/203.2.301. Bibcode: 1983MNRAS.203..301H. 
• King, D. L. (1985). "Atmospheric Extinction at the Roque de los Muchachos Observatory, La Palma". RGO/La Palma Technical Note 31. 
• McCall, M. L. (2004). "On Determining Extinction from Reddening". The Astronomical Journal. 128: 2144–2169. http://adsabs.harvard.edu/abs/2004AJ....128.2144M
• Rouleau, F.; Henning, T.; Stognienko, R. (1997). "Constraints on the properties of the 2175Å interstellar feature carrier". Astronomy and Astrophysics 322: 633–645. Bibcode: 1997A&A...322..633R. 

0.00 (0 votes)