Auxetics

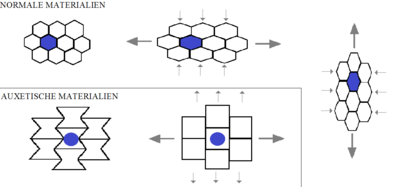
Auxetics are structures or materials that have a negative Poisson's ratio. When stretched, they become thicker perpendicular to the applied force. This occurs due to their particular internal structure and the way this deforms when the sample is uniaxially loaded. Auxetics can be single molecules, crystals, or a particular structure of macroscopic matter.^[1][2]

Such materials and structures are expected to have mechanical properties such as high energy absorption and fracture resistance. Auxetics may be useful in applications such as body armor,^[3] packing material, knee and elbow pads, robust shock absorbing material, and sponge mops.

History

The term auxetic derives from the Greek word auxetikos (αὐξητικός) which means 'that which tends to increase' and has its root in the word auxesis (αὔξησις), meaning 'increase' (noun). This terminology was coined by Professor Ken Evans of the University of Exeter.^[4][2] One of the first artificially produced auxetic materials, the RFS structure (diamond-fold structure), was invented in 1978 by the Berlin researcher K. Pietsch. Although he did not use the term auxetics, he describes for the first time the underlying lever mechanism and its non-linear mechanical reaction so he is therefore considered the inventor of the auxetic net. The earliest published example of a material with negative Poisson's constant is due to A. G. Kolpakov in 1985, "Determination of the average characteristics of elastic frameworks"; the next synthetic auxetic material was described in Science in 1987, entitled "Foam structures with a Negative Poisson's Ratio"^[1] by R.S. Lakes from the University of Wisconsin Madison. The use of the word auxetic to refer to this property probably began in 1991.^[5] Recently, cells were shown to display a biological version of auxeticity under certain conditions. ^[6]

Designs of composites with inverted hexagonal periodicity cell (auxetic hexagon), possessing negative Poisson ratios, were published in 1985.^[7]

Properties

Typically, auxetic materials have low density, which is what allows the hinge-like areas of the auxetic microstructures to flex.^[8]

At the macroscale, auxetic behaviour can be illustrated with an inelastic string wound around an elastic cord. When the ends of the structure are pulled apart, the inelastic string straightens while the elastic cord stretches and winds around it, increasing the structure's effective volume. Auxetic behaviour at the macroscale can also be employed for the development of products with enhanced characteristics such as footwear based on the auxetic rotating triangles structures developed by Grima and Evans^[9][10][11] and prosthetic feet with human-like toe joint properties.^[12]

Auxeticity is also common in biological materials. The origin of auxeticity is very different in biological materials than the materials discussed above. One of the example is nuclei of mouse embryonic stem cells in transition state. A model has been developed by Tripathi et. al ^[13] to explain it.

Examples

In footwear, auxetic design allows the sole to expand in size while walking or running, thereby increasing flexibility.

Examples of auxetic materials include:

• Auxetic polyurethane foam^[14][15]
• Nuclei of mouse embryonic stem cells in exiting pluripotent state ^[13]
• α-Cristobalite.^[16]
• Certain states of crystalline materials: Li, Na, K, Cu, Rb, Ag, Fe, Ni, Co, Cs, Au, Be, Ca, Zn, Sr, Sb, MoS[math]\displaystyle{ _2 }[/math], BAsO[math]\displaystyle{ _4 }[/math] and other.^[17][18][19]
• Certain rocks and minerals^[20]
• Graphene, which can be made auxetic through the introduction of vacancy defects^[21][22]
• Carbon diamond-like phases^[23]
• Noncarbon nanotubes^[24][25]
• Living bone tissue (although this is only suspected)^[20]
• Tendons within their normal range of motion.^[26]
• Specific variants of polytetrafluorethylene polymers such as Gore-Tex^[27]
• Several types of origami folds like the Diamond-Folding-Structure (RFS), the herringbone-fold-structure (FFS) or the miura fold,^[28][29] and other periodic patterns derived from it.^[30][31]

Production of auxetic metamaterials through the introduction of patterned microstructural cuts using direct laser cutting. The thin rubber surface with perforated architecture covers a spherical surface (orange)^[32]

• Tailored structures designed to exhibit special designed Poisson's ratios.^{[33][34][35][36][37][38]}
• Chain organic molecules. Recent researches revealed that organic crystals like n-paraffins and similar to them may demonstrate an auxetic behavior.^[39]

See also

• Acoustic metamaterial
• Mechanical metamaterial
• Metamaterial
• Parallelogon
• Zetix, a type of commercially manufactured auxetic material

References

External links

• Materials with negative Poisson's ratio
• Auxetic foam in youtube
• General Information about Auxetic Materials

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Auxetics. Read more