Free energy principle

The free energy principle is a theoretical framework suggesting that the brain reduces surprise or uncertainty by making predictions based on internal models and updating them using sensory input. It highlights the brain's objective of aligning its internal model with the external world to enhance prediction accuracy. This principle integrates Bayesian inference with active inference, where actions are guided by predictions and sensory feedback refines them. It has wide-ranging implications for comprehending brain function, perception, and action.^[1]

Overview

In biophysics and cognitive science, the free energy principle is a mathematical principle describing a formal account of the representational capacities of physical systems: that is, why things that exist look as if they track properties of the systems to which they are coupled.^[2]

It establishes that the dynamics of physical systems minimise a quantity known as surprisal (which is just the negative log probability of some outcome); or equivalently, its variational upper bound, called free energy. The principle is used especially in Bayesian approaches to brain function, but also some approaches to artificial intelligence; it is formally related to variational Bayesian methods and was originally introduced by Karl Friston as an explanation for embodied perception-action loops in neuroscience.^[3]

The free energy principle models the behaviour of systems that are distinct from, but coupled to, another system (e.g., an embedding environment), where the degrees of freedom that implement the interface between the two systems is known as a Markov blanket. More formally, the free energy principle says that if a system has a "particular partition" (i.e., into particles, with their Markov blankets), then subsets of that system will track the statistical structure of other subsets (which are known as internal and external states or paths of a system).

The free energy principle is based on the Bayesian idea of the brain as an “inference engine.” Under the free energy principle, systems pursue paths of least surprise, or equivalently, minimize the difference between predictions based on their model of the world and their sense and associated perception. This difference is quantified by variational free energy and is minimized by continuous correction of the world model of the system, or by making the world more like the predictions of the system. By actively changing the world to make it closer to the expected state, systems can also minimize the free energy of the system. Friston assumes this to be the principle of all biological reaction.^[4] Friston also believes his principle applies to mental disorders as well as to artificial intelligence. AI implementations based on the active inference principle have shown advantages over other methods.^[4]

The free energy principle is a mathematical principle of information physics: much like the principle of maximum entropy or the principle of least action, it is true on mathematical grounds. To attempt to falsify the free energy principle is a category mistake, akin to trying to falsify calculus by making empirical observations. (One cannot invalidate a mathematical theory in this way; instead, one would need to derive a formal contradiction from the theory.) In a 2018 interview, Friston explained what it entails for the free energy principle to not be subject to falsification: "I think it is useful to make a fundamental distinction at this point—that we can appeal to later. The distinction is between a state and process theory; i.e., the difference between a normative principle that things may or may not conform to, and a process theory or hypothesis about how that principle is realized. Under this distinction, the free energy principle stands in stark distinction to things like predictive coding and the Bayesian brain hypothesis. This is because the free energy principle is what it is — a principle. Like Hamilton's principle of stationary action, it cannot be falsified. It cannot be disproven. In fact, there’s not much you can do with it, unless you ask whether measurable systems conform to the principle. On the other hand, hypotheses that the brain performs some form of Bayesian inference or predictive coding are what they are—hypotheses. These hypotheses may or may not be supported by empirical evidence."^[5] There are many examples of these hypotheses being supported by empirical evidence.^[6]

Background

The notion that self-organising biological systems – like a cell or brain – can be understood as minimising variational free energy is based upon Helmholtz’s work on unconscious inference^[7] and subsequent treatments in psychology^[8] and machine learning.^[9] Variational free energy is a function of observations and a probability density over their hidden causes. This variational density is defined in relation to a probabilistic model that generates predicted observations from hypothesized causes. In this setting, free energy provides an approximation to Bayesian model evidence.^[10] Therefore, its minimisation can be seen as a Bayesian inference process. When a system actively makes observations to minimise free energy, it implicitly performs active inference and maximises the evidence for its model of the world.

However, free energy is also an upper bound on the self-information of outcomes, where the long-term average of surprise is entropy. This means that if a system acts to minimise free energy, it will implicitly place an upper bound on the entropy of the outcomes – or sensory states – it samples.^[11][12]

Relationship to other theories

Active inference is closely related to the good regulator theorem^[13] and related accounts of self-organisation,^[14][15] such as self-assembly, pattern formation, autopoiesis^[16] and practopoiesis.^[17] It addresses the themes considered in cybernetics, synergetics^[18] and embodied cognition. Because free energy can be expressed as the expected energy of observations under the variational density minus its entropy, it is also related to the maximum entropy principle.^[19] Finally, because the time average of energy is action, the principle of minimum variational free energy is a principle of least action. Active inference allowing for scale invariance has also been applied to other theories and domains. For instance, it has been applied to sociology,^{[20][21][22][23]} linguistics and communication,^[24][25][26] semiotics,^[27][28] and epidemiology ^[29] among others.

Negative free energy is formally equivalent to the evidence lower bound, which is commonly used in machine learning to train generative models, such as variational autoencoders.

Action and perception

Figure 1: These schematics illustrate the partition of states into the internal states [math]\displaystyle{ \mu(t) }[/math] and external (hidden, latent) states [math]\displaystyle{ \psi(t) }[/math] that are separated by a Markov blanket – comprising sensory states [math]\displaystyle{ s(t) }[/math] and active states [math]\displaystyle{ a(t) }[/math]. The upper panel shows exactly the same dependencies but rearranged so that the internal states are associated with the intracellular states of a cell, while the sensory states become the surface states of the cell membrane overlying active states (e.g., the actin filaments of the cytoskeleton). The lower panel shows this partition as it would be applied to action and perception in the brain; where active and internal states minimise a free energy functional of sensory states. The ensuing self-organisation of internal states then correspond to perception, while action couples brain states back to external states.

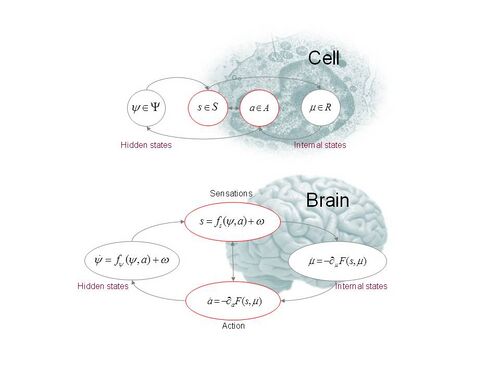
Active inference applies the techniques of approximate Bayesian inference to infer the causes of sensory data from a 'generative' model of how that data is caused and then uses these inferences to guide action. Bayes' rule characterizes the probabilistically optimal inversion of such a causal model, but applying it is typically computationally intractable, leading to the use of approximate methods. In active inference, the leading class of such approximate methods are variational methods, for both practical and theoretical reasons: practical, as they often lead to simple inference procedures; and theoretical, because they are related to fundamental physical principles, as discussed above.

These variational methods proceed by minimizing an upper bound on the divergence between the Bayes-optimal inference (or 'posterior') and its approximation according to the method. This upper bound is known as the free energy, and we can accordingly characterize perception as the minimization of the free energy with respect to inbound sensory information, and action as the minimization of the same free energy with respect to outbound action information. This holistic dual optimization is characteristic of active inference, and the free energy principle is the hypothesis that all systems which perceive and act can be characterized in this way.

In order to exemplify the mechanics of active inference via the free energy principle, a generative model must be specified, and this typically involves a collection of probability density functions which together characterize the causal model. One such specification is as follows. The system is modelled as inhabiting a state space [math]\displaystyle{ X }[/math], in the sense that its states form the points of this space. The state space is then factorized according to [math]\displaystyle{ X = \Psi\times S\times A\times R }[/math], where [math]\displaystyle{ \Psi }[/math] is the space of 'external' states that are 'hidden' from the agent (in the sense of not being directly perceived or accessible), [math]\displaystyle{ S }[/math] is the space of sensory states that are directly perceived by the agent, [math]\displaystyle{ A }[/math] is the space of the agent's possible actions, and [math]\displaystyle{ R }[/math] is a space of 'internal' states that are private to the agent.

Keeping with the Figure 1, note that in the following the [math]\displaystyle{ \dot{\psi}, \psi, s, a }[/math] and [math]\displaystyle{ \mu }[/math] are functions of (continuous) time [math]\displaystyle{ t }[/math]. The generative model is the specification of the following density functions:

• A sensory model, [math]\displaystyle{ p_S:S \times \Psi\times A \to \mathbb{R} }[/math], often written as [math]\displaystyle{ p_S(s \mid \psi, a) }[/math], characterizing the likelihood of sensory data given external states and actions;
• a stochastic model of the environmental dynamics, [math]\displaystyle{ p_\Psi: \Psi \times \Psi \times A \to \mathbb{R} }[/math], often written [math]\displaystyle{ p_\Psi(\dot{\psi} \mid \psi, a) }[/math], characterizing how the external states are expected by the agent to evolve over time [math]\displaystyle{ t }[/math], given the agent's actions;
• an action model, [math]\displaystyle{ p_A: A \times R \times S \to \mathbb{R} }[/math], written [math]\displaystyle{ p_A(a \mid \mu, s) }[/math], characterizing how the agent's actions depend upon its internal states and sensory data; and
• an internal model, [math]\displaystyle{ p_R: R \times S \to \mathbb{R} }[/math], written [math]\displaystyle{ p_R(\mu \mid s) }[/math], characterizing how the agent's internal states depend upon its sensory data.

These density functions determine the factors of a "joint model", which represents the complete specification of the generative model, and which can be written as

[math]\displaystyle{ p_{\text{Bayes}}(\dot{\psi}, s, a, \mu \mid \psi) = p_S(s \mid \psi, a)p_\Psi(\dot{\psi} \mid \psi, a)p_A(a \mid \mu, s)p_R(\mu \mid s) }[/math].

Bayes' rule then determines the "posterior density" [math]\displaystyle{ p(\dot{\psi} | s, a, \mu, \psi) }[/math], which expresses a probabilistically optimal belief about the external state [math]\displaystyle{ \psi }[/math] given the preceding state and the agent's actions, sensory signals, and internal states. Since computing [math]\displaystyle{ p_{\text{Bayes}} }[/math] is computationally intractable, the free energy principle asserts the existence of a "variational density" [math]\displaystyle{ q(\dot{\psi} | s, a, \mu, \psi) }[/math], where [math]\displaystyle{ q }[/math] is an approximation to [math]\displaystyle{ p_{\text{Bayes}} }[/math]. One then defines the free energy as

[math]\displaystyle{ \begin{align} \underset{\mathrm{free-energy}} {\underbrace{F(\mu, a\, ; s)}} &= \underset{\text{expected energy}} {\underbrace{ \mathbb{E}_{q(\dot{\psi})}[-\log p(\dot{\psi}, s, a, \mu \mid \psi)]}} - \underset{\mathrm{entropy}} {\underbrace{ \mathbb{H}[q(\dot{\psi} \mid s, a, \mu, \psi)]}}\\ &= \underset{\mathrm{surprise}} {\underbrace{ -\log p(s)}} + \underset{\mathrm{divergence}} {\underbrace{ \mathbb{KL}[q(\dot{\psi} \mid s, a, \mu, \psi) \parallel p_{\text{Bayes}}(\dot{\psi} \mid s, a, \mu, \psi)]}} \\ &\geq \underset{\mathrm{surprise}} {\underbrace{ -\log p(s)}} \end{align} }[/math]

and defines action and perception as the joint optimization problem

[math]\displaystyle{ \begin{align} \mu^* &= \underset{\mu}{\operatorname{arg\,min}} \{ F(\mu, a \,;\, s)) \} \\ a^* &= \underset{a}{\operatorname{arg\,min}} \{ F(\mu^*, a \,;\, s) \} \end{align} }[/math]

where the internal states [math]\displaystyle{ \mu }[/math] are typically taken to encode the parameters of the 'variational' density [math]\displaystyle{ q }[/math] and hence the agent's "best guess" about the posterior belief over [math]\displaystyle{ \Psi }[/math]. Note that the free energy is also an upper bound on a measure of the agent's (marginal, or average) sensory surprise, and hence free energy minimization is often motivated by the minimization of surprise.

Free energy minimisation

Free energy minimisation and self-organisation

Free energy minimisation has been proposed as a hallmark of self-organising systems when cast as random dynamical systems.^[30] This formulation rests on a Markov blanket (comprising action and sensory states) that separates internal and external states. If internal states and action minimise free energy, then they place an upper bound on the entropy of sensory states:

[math]\displaystyle{ \lim_{T\to\infty} \frac{1}{T} \underset{\text{free-action}} {\underbrace{\int_0^T F(s(t),\mu (t))\,dt}} \ge \lim_{T\to\infty} \frac{1}{T} \int_0^T \underset{\text{surprise}}{\underbrace{-\log p(s(t)\mid m)}} \, dt = H[p(s\mid m)] }[/math]

This is because – under ergodic assumptions – the long-term average of surprise is entropy. This bound resists a natural tendency to disorder – of the sort associated with the second law of thermodynamics and the fluctuation theorem. However, formulating a unifying principle for the life sciences in terms of concepts from statistical physics, such as random dynamical system, non-equilibrium steady state and ergodicity, places substantial constraints on the theoretical and empirical study of biological systems with the risk of obscuring all features that make biological systems interesting kinds of self-organizing systems.^[31]

Free energy minimisation and Bayesian inference

All Bayesian inference can be cast in terms of free energy minimisation^{[32][failed verification]}. When free energy is minimised with respect to internal states, the Kullback–Leibler divergence between the variational and posterior density over hidden states is minimised. This corresponds to approximate Bayesian inference – when the form of the variational density is fixed – and exact Bayesian inference otherwise. Free energy minimisation therefore provides a generic description of Bayesian inference and filtering (e.g., Kalman filtering). It is also used in Bayesian model selection, where free energy can be usefully decomposed into complexity and accuracy:

[math]\displaystyle{ \underset{\text{free-energy}} {\underbrace{ F(s,\mu)}} = \underset{\text{complexity}} {\underbrace{ D_\mathrm{KL}[q(\psi\mid\mu)\parallel p(\psi\mid m)]}} - \underset{\mathrm{accuracy}} {\underbrace{E_q[\log p(s\mid\psi,m)]}} }[/math]

Models with minimum free energy provide an accurate explanation of data, under complexity costs (c.f., Occam's razor and more formal treatments of computational costs^[33]). Here, complexity is the divergence between the variational density and prior beliefs about hidden states (i.e., the effective degrees of freedom used to explain the data).

Free energy minimisation and thermodynamics

Variational free energy is an information-theoretic functional and is distinct from thermodynamic (Helmholtz) free energy.^[34] However, the complexity term of variational free energy shares the same fixed point as Helmholtz free energy (under the assumption the system is thermodynamically closed but not isolated). This is because if sensory perturbations are suspended (for a suitably long period of time), complexity is minimised (because accuracy can be neglected). At this point, the system is at equilibrium and internal states minimise Helmholtz free energy, by the principle of minimum energy.^[35]

Free energy minimisation and information theory

Free energy minimisation is equivalent to maximising the mutual information between sensory states and internal states that parameterise the variational density (for a fixed entropy variational density). This relates free energy minimization to the principle of minimum redundancy ^[36][12]

Free energy minimisation in neuroscience

Free energy minimisation provides a useful way to formulate normative (Bayes optimal) models of neuronal inference and learning under uncertainty^[37] and therefore subscribes to the Bayesian brain hypothesis.^[38] The neuronal processes described by free energy minimisation depend on the nature of hidden states: [math]\displaystyle{ \Psi = X \times \Theta \times \Pi }[/math] that can comprise time-dependent variables, time-invariant parameters and the precision (inverse variance or temperature) of random fluctuations. Minimising variables, parameters, and precision correspond to inference, learning, and the encoding of uncertainty, respectively.

Perceptual inference and categorisation

Free energy minimisation formalises the notion of unconscious inference in perception^[7][9] and provides a normative (Bayesian) theory of neuronal processing. The associated process theory of neuronal dynamics is based on minimising free energy through gradient descent. This corresponds to generalised Bayesian filtering (where ~ denotes a variable in generalised coordinates of motion and [math]\displaystyle{ D }[/math] is a derivative matrix operator):^[39]

[math]\displaystyle{ \dot{\tilde{\mu}} = D \tilde{\mu} - \partial_{\mu}F(s,\mu)\Big|_{\mu = \tilde{\mu}} }[/math]

Usually, the generative models that define free energy are non-linear and hierarchical (like cortical hierarchies in the brain). Special cases of generalised filtering include Kalman filtering, which is formally equivalent to predictive coding^[40] – a popular metaphor for message passing in the brain. Under hierarchical models, predictive coding involves the recurrent exchange of ascending (bottom-up) prediction errors and descending (top-down) predictions^[41] that is consistent with the anatomy and physiology of sensory^[42] and motor systems.^[43]

Perceptual learning and memory

In predictive coding, optimising model parameters through a gradient descent on the time integral of free energy (free action) reduces to associative or Hebbian plasticity and is associated with synaptic plasticity in the brain.

Perceptual precision, attention and salience

Optimizing the precision parameters corresponds to optimizing the gain of prediction errors (c.f., Kalman gain). In neuronally plausible implementations of predictive coding,^[41] this corresponds to optimizing the excitability of superficial pyramidal cells and has been interpreted in terms of attentional gain.^[44]

Simulation of the results achieved from a selective attention task carried out by the Bayesian reformulation of the SAIM entitled PE-SAIM in multiple objects environment. The graphs show the time course of the activation for the FOA and the two template units in the Knowledge Network.

With regard to the top-down vs. bottom-up controversy, which has been addressed as a major open problem of attention, a computational model has succeeded in illustrating the circular nature of the interplay between top-down and bottom-up mechanisms. Using an established emergent model of attention, namely SAIM, the authors proposed a model called PE-SAIM, which, in contrast to the standard version, approaches selective attention from a top-down position. The model takes into account the transmission of prediction errors to the same level or a level above, in order to minimise the energy function that indicates the difference between the data and its cause, or, in other words, between the generative model and the posterior. To increase validity, they also incorporated neural competition between stimuli into their model. A notable feature of this model is the reformulation of the free energy function only in terms of prediction errors during task performance:

[math]\displaystyle{ \dfrac{\partial E^{total}(Y^{VP},X^{SN},x^{CN},y^{KN})}{\partial y^{SN}_{mn}}=x^{CN}_{mn}-b^{CN}\varepsilon^{CN}_{nm}+b^{CN}\sum_{k}(\varepsilon^{KN}_{knm}) }[/math]

where [math]\displaystyle{ E^{total} }[/math] is the total energy function of the neural networks entail, and [math]\displaystyle{ \varepsilon^{KN}_{knm} }[/math] is the prediction error between the generative model (prior) and posterior changing over time.^[45] Comparing the two models reveals a notable similarity between their respective results while also highlighting a remarkable discrepancy, whereby – in the standard version of the SAIM – the model's focus is mainly upon the excitatory connections, whereas in the PE-SAIM, the inhibitory connections are leveraged to make an inference. The model has also proved to be fit to predict the EEG and fMRI data drawn from human experiments with high precision. In the same vein, Yahya et al. also applied the free energy principle to propose a computational model for template matching in covert selective visual attention that mostly relies on SAIM.^[46] According to this study, the total free energy of the whole state-space is reached by inserting top-down signals in the original neural networks, whereby we derive a dynamical system comprising both feed-forward and backward prediction error.

Active inference

When gradient descent is applied to action [math]\displaystyle{ \dot{a} = -\partial_aF(s,\tilde{\mu}) }[/math], motor control can be understood in terms of classical reflex arcs that are engaged by descending (corticospinal) predictions. This provides a formalism that generalizes the equilibrium point solution – to the degrees of freedom problem^[47] – to movement trajectories.

Active inference and optimal control

Active inference is related to optimal control by replacing value or cost-to-go functions with prior beliefs about state transitions or flow.^[48] This exploits the close connection between Bayesian filtering and the solution to the Bellman equation. However, active inference starts with (priors over) flow [math]\displaystyle{ f = \Gamma \cdot \nabla V + \nabla \times W }[/math] that are specified with scalar [math]\displaystyle{ V(x) }[/math] and vector [math]\displaystyle{ W(x) }[/math] value functions of state space (c.f., the Helmholtz decomposition). Here, [math]\displaystyle{ \Gamma }[/math] is the amplitude of random fluctuations and cost is [math]\displaystyle{ c(x) = f \cdot \nabla V + \nabla \cdot \Gamma \cdot V }[/math]. The priors over flow [math]\displaystyle{ p(\tilde{x}\mid m) }[/math] induce a prior over states [math]\displaystyle{ p(x\mid m) = \exp (V(x)) }[/math] that is the solution to the appropriate forward Kolmogorov equations.^[49] In contrast, optimal control optimises the flow, given a cost function, under the assumption that [math]\displaystyle{ W = 0 }[/math] (i.e., the flow is curl free or has detailed balance). Usually, this entails solving backward Kolmogorov equations.^[50]

Active inference and optimal decision (game) theory

Optimal decision problems (usually formulated as partially observable Markov decision processes) are treated within active inference by absorbing utility functions into prior beliefs. In this setting, states that have a high utility (low cost) are states an agent expects to occupy. By equipping the generative model with hidden states that model control, policies (control sequences) that minimise variational free energy lead to high utility states.^[51]

Neurobiologically, neuromodulators such as dopamine are considered to report the precision of prediction errors by modulating the gain of principal cells encoding prediction error.^[52] This is closely related to – but formally distinct from – the role of dopamine in reporting prediction errors per se^[53] and related computational accounts.^[54]

Active inference and cognitive neuroscience

Active inference has been used to address a range of issues in cognitive neuroscience, brain function and neuropsychiatry, including action observation,^[55] mirror neurons,^[56] saccades and visual search,^[57][58] eye movements,^[59] sleep,^[60] illusions,^[61] attention,^[44] action selection,^[52] consciousness,^[62][63] hysteria^[64] and psychosis.^[65] Explanations of action in active inference often depend on the idea that the brain has 'stubborn predictions' that it cannot update, leading to actions that cause these predictions to come true.^[66]

See also

• Action-specific perception
• Philosophy:Affordance – Possibility of an action on an object or environment
• Autopoiesis – Systems concept which entails automatic reproduction and maintenance
• Bayesian approaches to brain function – Explaining the brain's abilities through statistical principles
• Constructal law - Law of design evolution in nature, animate and inanimate
• Decision theory – Branch of applied probability theory
• Embodied cognition – Interdisciplinary theory
• Physics:Entropic force – Physical force that originates from thermodynamics instead of fundamental interactions
• Physics:Principle of minimum energy
• Info-metrics – Interdisciplinary approach to scientific modelling and information processing
• Optimal control – Mathematical way of attaining a desired output from a dynamic system
• Adaptive system, also known as Practopoiesis
• Philosophy:Predictive coding – Theory of brain function
• Physics:Self-organization – Process of creating order by local interactions
• Synergetics (Haken)
• Variational Bayesian methods – Mathematical methods used in Bayesian inference and machine learning

References

External links

• Behavioral and Brain Sciences (by Andy Clark)

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Free energy principle. Read more