Chebyshev polynomials

The Chebyshev polynomials are two sequences of polynomials related to the cosine and sine functions, notated as ${\displaystyle T_n(x)}$ and ${\displaystyle U_n(x)}$. They can be defined in several equivalent ways, one of which starts with trigonometric functions:

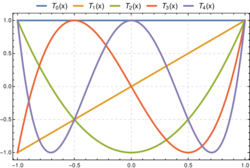
The Chebyshev polynomials of the first kind ${\displaystyle T_n}$ are defined by:

${\displaystyle T_n(\cos \theta )=\cos (n\theta ).}$

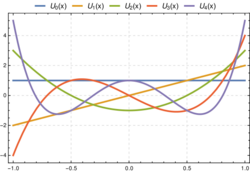
Similarly, the Chebyshev polynomials of the second kind ${\displaystyle U_n}$ are defined by:

${\displaystyle U_n(\cos \theta )\sin \theta =\sin ((n+1)\theta ).}$

That these expressions define polynomials in ${\displaystyle \cos \theta }$ may not be obvious at first sight but follows by rewriting ${\displaystyle \cos (n\theta )}$ and ${\displaystyle \sin ((n+1)\theta )}$ using de Moivre's formula or by using the angle sum formulas for ${\displaystyle \cos }$ and ${\displaystyle \sin }$ repeatedly. For example, the double angle formulas, which follow directly from the angle sum formulas, may be used to obtain ${\displaystyle T_2(\cos \theta )=\cos (2\theta )=2{\cos }^2\theta -1}$ and ${\displaystyle U_1(\cos \theta )\sin \theta =\sin (2\theta )=2\cos \theta \sin \theta }$, which are respectively a polynomial in ${\displaystyle \cos \theta }$ and a polynomial in ${\displaystyle \cos \theta }$ multiplied by ${\displaystyle \sin \theta }$. Hence ${\displaystyle T_2(x)=2x^2-1}$ and ${\displaystyle U_1(x)=2x}$.

An important and convenient property of the T_n(x) is that they are orthogonal with respect to the inner product:

${\displaystyle ⟨f,g⟩={\int }_{-1}^{1}f(x)g(x)\frac{\mathrm{d}x}{\sqrt{1-x^2}},}$

and U_n(x) are orthogonal with respect to another, analogous inner product, given below.

The Chebyshev polynomials T_n are polynomials with the largest possible leading coefficient whose absolute value on the interval [−1, 1] is bounded by 1. They are also the "extremal" polynomials for many other properties.^[1]

In 1952, Cornelius Lanczos showed that the Chebyshev polynomials are important in approximation theory for the solution of linear systems;^[2] the roots of T_n(x), which are also called Chebyshev nodes, are used as matching points for optimizing polynomial interpolation. The resulting interpolation polynomial minimizes the problem of Runge's phenomenon and provides an approximation that is close to the best polynomial approximation to a continuous function under the maximum norm, also called the "minimax" criterion. This approximation leads directly to the method of Clenshaw–Curtis quadrature.

These polynomials were named after Pafnuty Chebyshev.^[3] The letter T is used because of the alternative transliterations of the name Chebyshev as Tchebycheff, Tchebyshev (French) or Tschebyschow (German).

Definitions

Recurrence definition

The Chebyshev polynomials of the first kind are obtained from the recurrence relation:

${\displaystyle \begin{array}{rl}{T}_0(x)& =1\\ T_1(x)& =x\\ T_{n+1}(x)& =2x{T}_n(x)-T_{n-1}(x).\end{array}}$

The recurrence also allows to represent them explicitly as the determinant of a tridiagonal matrix of size ${\displaystyle k\times k}$:

${\displaystyle T_k(x)=det\left[\begin{array}{ccccc}x& 1& 0& \cdots & 0\\ 1& 2x& 1& \ddots & ⋮\\ 0& 1& 2x& \ddots & 0\\ ⋮& \ddots & \ddots & \ddots & 1\\ 0& \cdots & 0& 1& 2x\end{array}\right]}$

The ordinary generating function for T_n is:

${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{T}_n(x)t^n=\frac{1-tx}{1-2tx+t^2}.}$

There are several other generating functions for the Chebyshev polynomials; the exponential generating function is:

${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{T}_n(x)\frac{t^n}{n!}=\frac{1}{2}(e^{t(x-\sqrt{x^2-1})}+e^{t(x+\sqrt{x^2-1})})=e^{tx}\cosh \left(t\sqrt{x^2-1}\right).}$

The generating function relevant for 2-dimensional potential theory and multipole expansion is:

${\displaystyle \sum _{n=1}^{\mathrm{\infty }}{T}_n(x)\frac{t^n}{n}=\ln \left(\frac{1}{\sqrt{1-2tx+t^2}}\right).}$

The Chebyshev polynomials of the second kind are defined by the recurrence relation:

${\displaystyle \begin{array}{rl}{U}_0(x)& =1\\ U_1(x)& =2x\\ U_{n+1}(x)& =2x{U}_n(x)-U_{n-1}(x).\end{array}}$

Notice that the two sets of recurrence relations are identical, except for ${\displaystyle T_1(x)=x}$ vs. ${\displaystyle U_1(x)=2x}$. The ordinary generating function for U_n is:

${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{U}_n(x)t^n=\frac{1}{1-2tx+t^2},}$

and the exponential generating function is:

${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{U}_n(x)\frac{t^n}{n!}=e^{tx}(\cosh \left(t\sqrt{x^2-1}\right)+\frac{x}{\sqrt{x^2-1}}\sinh \left(t\sqrt{x^2-1}\right)).}$

Trigonometric definition

As described in the introduction, the Chebyshev polynomials of the first kind can be defined as the unique polynomials satisfying:

${\displaystyle T_n(x)=\{\begin{array}{ll}\cos (n\arccos x)& \text{ if }|x|\le 1\\ \cosh (n\mathrm{arcosh}x)& \text{ if }x\ge 1\\ (-1{)}^n\cosh (n\mathrm{arcosh}(-x))& \text{ if }x\le -1\end{array}}$

or, in other words, as the unique polynomials satisfying:

${\displaystyle T_n(\cos \theta )=\cos (n\theta )}$

for n = 0, 1, 2, 3, ….

The polynomials of the second kind satisfy:

${\displaystyle U_{n-1}(\cos \theta )\sin \theta =\sin (n\theta ),}$

or

${\displaystyle U_n(\cos \theta )=\frac{\sin ((n+1)\theta )}{\sin \theta },}$

which is structurally quite similar to the Dirichlet kernel D_n(x):

${\displaystyle D_n(x)=\frac{\sin ((2n+1){\displaystyle \frac{x}{2}})}{\sin {\displaystyle \frac{x}{2}}}=U_{2n}(\cos \frac{x}{2}).}$

(The Dirichlet kernel, in fact, coincides with what is now known as the Chebyshev polynomial of the fourth kind.)

An equivalent way to state this is via exponentiation of a complex number: given a complex number z = a + bi with absolute value of one:

${\displaystyle z^n=T_n(a)+ib{U}_{n-1}(a).}$

Chebyshev polynomials can be defined in this form when studying trigonometric polynomials.^[4]

That cos nx is an nth-degree polynomial in cos x can be seen by observing that cos nx is the real part of one side of de Moivre's formula:

${\displaystyle \cos n\theta +i\sin n\theta =(\cos \theta +i\sin \theta {)}^n.}$

The real part of the other side is a polynomial in cos x and sin x, in which all powers of sin x are even and thus replaceable through the identity cos² x + sin² x = 1. By the same reasoning, sin nx is the imaginary part of the polynomial, in which all powers of sin x are odd and thus, if one factor of sin x is factored out, the remaining factors can be replaced to create a (n−1)st-degree polynomial in cos x.

Commuting polynomials definition

Chebyshev polynomials can also be characterized by the following theorem:^[5]

If ${\displaystyle F_n(x)}$ is a family of monic polynomials with coefficients in a field of characteristic ${\displaystyle 0}$ such that ${\displaystyle \mathrm{deg}{F}_n(x)=n}$ and ${\displaystyle F_m(F_n(x))=F_n(F_m(x))}$ for all ${\displaystyle m}$ and ${\displaystyle n}$, then, up to a simple change of variables, either ${\displaystyle F_n(x)=x^n}$ for all ${\displaystyle n}$ or ${\displaystyle F_n(x)=2\ast T_n(x/2)}$ for all ${\displaystyle n}$.

Pell equation definition

The Chebyshev polynomials can also be defined as the solutions to the Pell equation:

${\displaystyle T_n(x{)}^2-(x^2-1)U_{n-1}(x{)}^2=1}$

in a ring R[x].^[6] Thus, they can be generated by the standard technique for Pell equations of taking powers of a fundamental solution:

${\displaystyle T_n(x)+U_{n-1}(x)\sqrt{x^2-1}={(x+\sqrt{x^2-1})}^n.}$

Relations between the two kinds of Chebyshev polynomials

The Chebyshev polynomials of the first and second kinds correspond to a complementary pair of Lucas sequences Ṽ_n(P, Q) and Ũ_n(P, Q) with parameters P = 2x and Q = 1:

${\displaystyle \begin{array}{rl}{\tilde{U}}_n(2x,1)& =U_{n-1}(x),\\ {\tilde{V}}_n(2x,1)& =2T_n(x).\end{array}}$

It follows that they also satisfy a pair of mutual recurrence equations:^[7]

${\displaystyle \begin{array}{rl}{T}_{n+1}(x)& =x{T}_n(x)-(1-x^2)U_{n-1}(x),\\ U_{n+1}(x)& =x{U}_n(x)+T_{n+1}(x).\end{array}}$

The second of these may be rearranged using the recurrence definition for the Chebyshev polynomials of the second kind to give:

${\displaystyle T_n(x)=\frac{1}{2}(U_n(x)-U_{n-2}(x)).}$

Using this formula iteratively gives the sum formula:

${\displaystyle U_n(x)=\{\begin{array}{ll}2\sum _{\text{ odd }j}^n{T}_j(x)& \text{ for odd }n.\\ 2\sum _{\text{ even }j}^n{T}_j(x)-1& \text{ for even }n,\end{array}}$

while replacing ${\displaystyle U_n(x)}$ and ${\displaystyle U_{n-2}(x)}$ using the derivative formula for ${\displaystyle T_n(x)}$ gives the recurrence relationship for the derivative of ${\displaystyle T_n}$:

${\displaystyle 2T_n(x)=\frac{1}{n+1}\frac{\mathrm{d}}{\mathrm{d}x}{T}_{n+1}(x)-\frac{1}{n-1}\frac{\mathrm{d}}{\mathrm{d}x}{T}_{n-1}(x),n=2,3,\dots }$

This relationship is used in the Chebyshev spectral method of solving differential equations.

Turán's inequalities for the Chebyshev polynomials are:^[8]

${\displaystyle \begin{array}{rlrlrl}{T}_n(x{)}^2-T_{n-1}(x)T_{n+1}(x)& =1-x^2>0& & \text{ for }-1<x<1& & \text{ and }\\ U_n(x{)}^2-U_{n-1}(x)U_{n+1}(x)& =1>0.\end{array}}$

The integral relations are^{[7]:187(47)(48)[9]}

${\displaystyle \begin{array}{rl}{\int }_{-1}^1\frac{T_n(y)}{(y-x)\sqrt{1-y^2}}\mathrm{d}y& =\pi U_{n-1}(x),\\ {\int }_{-1}^1\frac{\sqrt{1-y^2}{U}_{n-1}(y)}{y-x}\mathrm{d}y& =-\pi T_n(x)\end{array}}$

where integrals are considered as principal value.

Explicit expressions

Different approaches to defining Chebyshev polynomials lead to different explicit expressions. The trigonometric definition gives an explicit formula as follows:

${\displaystyle \begin{array}{rl}{T}_n(x)& =\{\begin{array}{ll}\cos (n\arccos x)& \text{ for }-1\le x\le 1\\ \cosh (n\mathrm{arcosh}x)& \text{ for }1\le x\\ (-1{)}^n\cosh (n\mathrm{arcosh}(-x))& \text{ for }x\le -1\end{array}\end{array}}$

From this trigonometric form, the recurrence definition can be recovered by computing directly that the bases cases hold:

${\displaystyle T_0(\cos \theta )=\cos (0\theta )=1}$

and

${\displaystyle T_1(\cos \theta )=\cos \theta ,}$

and that the product-to-sum identity holds:

${\displaystyle 2\cos n\theta \cos \theta =\cos [(n+1)\theta ]+\cos [(n-1)\theta ].}$

Using the complex number exponentiation definition of the Chebyshev polynomial, one can derive the following expression:

${\displaystyle T_n(x)={\displaystyle \frac{1}{2}}((x-\sqrt{x^2-1}{)}^n+(x+\sqrt{x^2-1}{)}^n)\text{ for }x\in \mathbb{R}}$

${\displaystyle T_n(x)={\displaystyle \frac{1}{2}}((x-\sqrt{x^2-1}{)}^n+(x-\sqrt{x^2-1}{)}^{-n})\text{ for }x\in \mathbb{R}}$

The two are equivalent because ${\displaystyle (x+\sqrt{x^2-1})(x-\sqrt{x^2-1})=1}$.

An explicit form of the Chebyshev polynomial in terms of monomials x^k follows from de Moivre's formula:

${\displaystyle T_n(\cos (\theta ))=\mathrm{Re}(\cos n\theta +i\sin n\theta )=\mathrm{Re}((\cos \theta +i\sin \theta {)}^n),}$

where Re denotes the real part of a complex number. Expanding the formula, one gets:

${\displaystyle (\cos \theta +i\sin \theta {)}^n=\sum _{j=0}^n(\genfrac{}{}{0ex}{}{n}{j})i^j{\sin }^j\theta {\cos }^{n-j}\theta .}$

The real part of the expression is obtained from summands corresponding to even indices. Noting ${\displaystyle i^{2j}=(-1{)}^j}$ and ${\displaystyle {\sin }^{2j}\theta =(1-{\cos }^2\theta {)}^j}$, one gets the explicit formula:

${\displaystyle \cos n\theta =\sum _{j=0}^{\lfloor n/2\rfloor }(\genfrac{}{}{0ex}{}{n}{2j})({\cos }^2\theta -1{)}^j{\cos }^{n-2j}\theta ,}$

which in turn means that:

${\displaystyle T_n(x)=\sum _{j=0}^{\lfloor n/2\rfloor }(\genfrac{}{}{0ex}{}{n}{2j})(x^2-1{)}^j{x}^{n-2j}.}$

This can be written as a ₂F₁ hypergeometric function:

${\displaystyle \begin{array}{rl}{T}_n(x)& =\sum _{k=0}^{\lfloor \frac{n}{2}\rfloor }(\genfrac{}{}{0ex}{}{n}{2k}){(x^2-1)}^k{x}^{n-2k}\\ & =x^n\sum _{k=0}^{\lfloor \frac{n}{2}\rfloor }(\genfrac{}{}{0ex}{}{n}{2k}){(1-x^{-2})}^k\\ & =\frac{n}{2}\sum _{k=0}^{\lfloor \frac{n}{2}\rfloor }(-1{)}^k\frac{(n-k-1)!}{k!(n-2k)!}(2x{)}^{n-2k}\text{ for }n>0\\ \\ & =n\sum _{k=0}^n(-2{)}^k\frac{(n+k-1)!}{(n-k)!(2k)!}(1-x{)}^k\text{ for }n>0\\ \\ & ={}_2{F}_1(-n,n;\frac{1}{2};\frac{1}{2}(1-x))\end{array}}$

with inverse:^[10][11]

${\displaystyle x^n=2^{1-n}\underset{\genfrac{}{}{0ex}{}{j=0}{j\equiv n(\mathrm{mod}2)}}{\overset{n}{{\sum }^{\prime }}}(\genfrac{}{}{0ex}{}{n}{\frac{n-j}{2}})T_j(x),}$

where the prime at the summation symbol indicates that the contribution of j = 0 needs to be halved if it appears.

A related expression for T_n as a sum of monomials with binomial coefficients and powers of two is

${\displaystyle T_n\left(x\right)=\sum _{m=0}^{\lfloor \frac{n}{2}\rfloor }{(-1)}^m((\genfrac{}{}{0ex}{}{n-m}{m})+(\genfrac{}{}{0ex}{}{n-m-1}{n-2m}))\cdot 2^{n-2m-1}\cdot x^{n-2m}.}$

Similarly, U_n can be expressed in terms of hypergeometric functions:

${\displaystyle \begin{array}{rl}{U}_n(x)& =\frac{{(x+\sqrt{x^2-1})}^{n+1}-{(x-\sqrt{x^2-1})}^{n+1}}{2\sqrt{x^2-1}}\\ & =\sum _{k=0}^{\lfloor \frac{n}{2}\rfloor }(\genfrac{}{}{0ex}{}{n+1}{2k+1}){(x^2-1)}^k{x}^{n-2k}\\ & =x^n\sum _{k=0}^{\lfloor \frac{n}{2}\rfloor }(\genfrac{}{}{0ex}{}{n+1}{2k+1}){(1-x^{-2})}^k\\ & =\sum _{k=0}^{\lfloor \frac{n}{2}\rfloor }(\genfrac{}{}{0ex}{}{2k-(n+1)}{k})(2x{)}^{n-2k}& \text{ for }n>0\\ & =\sum _{k=0}^{\lfloor \frac{n}{2}\rfloor }(-1{)}^k(\genfrac{}{}{0ex}{}{n-k}{k})(2x{)}^{n-2k}& \text{ for }n>0\\ & =\sum _{k=0}^n(-2{)}^k\frac{(n+k+1)!}{(n-k)!(2k+1)!}(1-x{)}^k& \text{ for }n>0\\ & =(n+1){}_2{F}_1(-n,n+2;\frac{3}{2};\frac{1}{2}(1-x)).\end{array}}$

Properties

Symmetry

${\displaystyle \begin{array}{rl}{T}_n(-x)& =(-1{)}^n{T}_n(x)=\{\begin{array}{ll}{T}_n(x)& \text{ for }n\text{ even}\\ -T_n(x)& \text{ for }n\text{ odd}\end{array}\\ \\ U_n(-x)& =(-1{)}^n{U}_n(x)=\{\begin{array}{ll}{U}_n(x)& \text{ for }n\text{ even}\\ -U_n(x)& \text{ for }n\text{ odd}\end{array}\end{array}}$

That is, Chebyshev polynomials of even order have even symmetry and therefore contain only even powers of x. Chebyshev polynomials of odd order have odd symmetry and therefore contain only odd powers of x.

Roots and extrema

A Chebyshev polynomial of either kind with degree n has n different simple roots, called Chebyshev roots, in the interval [−1, 1]. The roots of the Chebyshev polynomial of the first kind are sometimes called Chebyshev nodes because they are used as nodes in polynomial interpolation. Using the trigonometric definition and the fact that:

${\displaystyle \cos ((2k+1)\frac{\pi }{2})=0}$

one can show that the roots of T_n are:

${\displaystyle x_k=\cos \left(\frac{\pi (k+1/2)}{n}\right),k=0,\dots ,n-1.}$

Similarly, the roots of U_n are:

${\displaystyle x_k=\cos \left(\frac{k}{n+1}\pi \right),k=1,\dots ,n.}$

The extrema of T_n on the interval −1 ≤ x ≤ 1 are located at:

${\displaystyle x_k=\cos \left(\frac{k}{n}\pi \right),k=0,\dots ,n.}$

One unique property of the Chebyshev polynomials of the first kind is that on the interval −1 ≤ x ≤ 1 all of the extrema have values that are either −1 or 1. Thus these polynomials have only two finite critical values, the defining property of Shabat polynomials. Both the first and second kinds of Chebyshev polynomial have extrema at the endpoints, given by:

${\displaystyle T_n(1)=1}$

${\displaystyle T_n(-1)=(-1{)}^n}$

${\displaystyle U_n(1)=n+1}$

${\displaystyle U_n(-1)=(-1{)}^n(n+1).}$

The extrema of ${\displaystyle T_n(x)}$ on the interval ${\displaystyle -1\le x\le 1}$ where ${\displaystyle n>0}$ are located at ${\displaystyle n+1}$ values of ${\displaystyle x}$. They are ${\displaystyle \pm 1}$, or ${\displaystyle \cos \left(\frac{2\pi k}{d}\right)}$ where ${\displaystyle d>2}$, ${\displaystyle d|2n}$, ${\displaystyle 0<k<d/2}$ and ${\displaystyle (k,d)=1}$, i.e., ${\displaystyle k}$ and ${\displaystyle d}$ are relatively prime numbers.

Specifically,^[12][13] when ${\displaystyle n}$ is even:

• ${\displaystyle T_n(x)=1}$ if ${\displaystyle x=\pm 1}$, or ${\displaystyle d>2}$ and ${\displaystyle 2n/d}$ is even. There are ${\displaystyle n/2+1}$ such values of ${\displaystyle x}$.
• ${\displaystyle T_n(x)=-1}$ if ${\displaystyle d>2}$ and ${\displaystyle 2n/d}$ is odd. There are ${\displaystyle n/2}$ such values of ${\displaystyle x}$.

When ${\displaystyle n}$ is odd:

• ${\displaystyle T_n(x)=1}$ if ${\displaystyle x=1}$, or ${\displaystyle d>2}$ and ${\displaystyle 2n/d}$ is even. There are ${\displaystyle (n+1)/2}$ such values of ${\displaystyle x}$.
• ${\displaystyle T_n(x)=-1}$ if ${\displaystyle x=-1}$, or ${\displaystyle d>2}$ and ${\displaystyle 2n/d}$ is odd. There are ${\displaystyle (n+1)/2}$ such values of ${\displaystyle x}$.

This result has been generalized to solutions of ${\displaystyle U_n(x)\pm 1=0}$,^[13] and to ${\displaystyle V_n(x)\pm 1=0}$ and ${\displaystyle W_n(x)\pm 1=0}$ for Chebyshev polynomials of the third and fourth kinds, respectively.^[14]

Differentiation and integration

The derivatives of the polynomials can be less than straightforward. By differentiating the polynomials in their trigonometric forms, it can be shown that:

${\displaystyle \begin{array}{rl}\frac{\mathrm{d}{T}_n}{\mathrm{d}x}& =n{U}_{n-1}\\ \frac{\mathrm{d}{U}_n}{\mathrm{d}x}& =\frac{(n+1)T_{n+1}-x{U}_n}{x^2-1}\\ \frac{{\mathrm{d}}^2{T}_n}{\mathrm{d}{x}^2}& =n\frac{n{T}_n-x{U}_{n-1}}{x^2-1}=n\frac{(n+1)T_n-U_n}{x^2-1}.\end{array}}$

The last two formulas can be numerically troublesome due to the division by zero (0/0 indeterminate form, specifically) at x = 1 and x = −1. By L'Hôpital's rule:

${\displaystyle \begin{array}{rl}{\frac{{\mathrm{d}}^2{T}_n}{\mathrm{d}{x}^2}|}_{x=1}& =\frac{n^4-n^2}{3},\\ {\frac{{\mathrm{d}}^2{T}_n}{\mathrm{d}{x}^2}|}_{x=-1}& =(-1{)}^n\frac{n^4-n^2}{3}.\end{array}}$

More generally,

${\displaystyle {\frac{d^p{T}_n}{d{x}^p}|}_{x=\pm 1}=(\pm 1{)}^{n+p}\prod _{k=0}^{p-1}\frac{n^2-k^2}{2k+1},}$

which is of great use in the numerical solution of eigenvalue problems.

Also, we have:

${\displaystyle \frac{{\mathrm{d}}^p}{\mathrm{d}{x}^p}{T}_n(x)=2^{p}n\underset{\genfrac{}{}{0ex}{}{0\le k\le n-p}{k\equiv n-p(\mathrm{mod}2)}}{{\sum }^{\prime }}(\genfrac{}{}{0ex}{}{\frac{n+p-k}{2}-1}{\frac{n-p-k}{2}})\frac{(\frac{n+p+k}{2}-1)!}{\left(\frac{n-p+k}{2}\right)!}{T}_k(x),p\ge 1,}$

where the prime at the summation symbols means that the term contributed by k = 0 is to be halved, if it appears.

Concerning integration, the first derivative of the T_n implies that:

${\displaystyle \int U_n\mathrm{d}x=\frac{T_{n+1}}{n+1}}$

and the recurrence relation for the first kind polynomials involving derivatives establishes that for n ≥ 2:

${\displaystyle \int T_n\mathrm{d}x=\frac{1}{2}(\frac{T_{n+1}}{n+1}-\frac{T_{n-1}}{n-1})=\frac{n{T}_{n+1}}{n^2-1}-\frac{x{T}_n}{n-1}.}$

The last formula can be further manipulated to express the integral of T_n as a function of Chebyshev polynomials of the first kind only:

${\displaystyle \begin{array}{rl}\int T_n\mathrm{d}x& =\frac{n}{n^2-1}{T}_{n+1}-\frac{1}{n-1}{T}_1{T}_n\\ & =\frac{n}{n^2-1}{T}_{n+1}-\frac{1}{2(n-1)}(T_{n+1}+T_{n-1})\\ & =\frac{1}{2(n+1)}{T}_{n+1}-\frac{1}{2(n-1)}{T}_{n-1}.\end{array}}$

Furthermore, we have:

${\displaystyle {\int }_{-1}^1{T}_n(x)\mathrm{d}x=\{\begin{array}{ll}\frac{(-1{)}^n+1}{1-n^2}& \text{ if }n\ne 1\\ 0& \text{ if }n=1.\end{array}}$

Products of Chebyshev polynomials

The Chebyshev polynomials of the first kind satisfy the relation:

${\displaystyle T_m(x)T_n(x)=\frac{1}{2}(T_{m+n}(x)+T_{|m-n|}(x)),\mathrm{\forall }m,n\ge 0,}$

which is easily proved from the product-to-sum formula for the cosine:

${\displaystyle 2\cos \alpha \cos \beta =\cos (\alpha +\beta )+\cos (\alpha -\beta ).}$

For n = 1 this results in the already known recurrence formula, just arranged differently, and with n = 2 it forms the recurrence relation for all even or all odd indexed Chebyshev polynomials (depending on the parity of the lowest m) which implies the evenness or oddness of these polynomials. Three more useful formulas for evaluating Chebyshev polynomials can be concluded from this product expansion:

${\displaystyle \begin{array}{rlrl}{T}_{2n}(x)& =2T_n^2(x)-T_0(x)& & =2T_n^2(x)-1,\\ T_{2n+1}(x)& =2T_{n+1}(x)T_n(x)-T_1(x)& & =2T_{n+1}(x)T_n(x)-x,\\ T_{2n-1}(x)& =2T_{n-1}(x)T_n(x)-T_1(x)& & =2T_{n-1}(x)T_n(x)-x.\end{array}}$

The polynomials of the second kind satisfy the similar relation:

${\displaystyle T_m(x)U_n(x)=\{\begin{array}{ll}\frac{1}{2}(U_{m+n}(x)+U_{n-m}(x)),& \text{ if }n\ge m-1,\\ \\ \frac{1}{2}(U_{m+n}(x)-U_{m-n-2}(x)),& \text{ if }n\le m-2.\end{array}}$

(with the definition U₋₁ ≡ 0 by convention ). They also satisfy:

${\displaystyle U_m(x)U_n(x)=\sum _{k=0}^n{U}_{m-n+2k}(x)=\sum _{\underset{\text{ step 2 }}{p=m-n}}^{m+n}{U}_p(x).}$

for m ≥ n. For n = 2 this recurrence reduces to:

${\displaystyle U_{m+2}(x)=U_2(x)U_m(x)-U_m(x)-U_{m-2}(x)=U_m(x)(U_2(x)-1)-U_{m-2}(x),}$

which establishes the evenness or oddness of the even or odd indexed Chebyshev polynomials of the second kind depending on whether m starts with 2 or 3.

Composition and divisibility properties

The trigonometric definitions of T_n and U_n imply the composition or nesting properties:^[15]

${\displaystyle \begin{array}{rl}{T}_{mn}(x)& =T_m(T_n(x)),\\ U_{mn-1}(x)& =U_{m-1}(T_n(x))U_{n-1}(x).\end{array}}$

For T_mn the order of composition may be reversed, making the family of polynomial functions T_n a commutative semigroup under composition.

Since T_m(x) is divisible by x if m is odd, it follows that T_mn(x) is divisible by T_n(x) if m is odd. Furthermore, U_mn−1(x) is divisible by U_n−1(x), and in the case that m is even, divisible by T_n(x)U_n−1(x).

Orthogonality

Both T_n and U_n form a sequence of orthogonal polynomials. The polynomials of the first kind T_n are orthogonal with respect to the weight:

${\displaystyle \frac{1}{\sqrt{1-x^2}},}$

on the interval [−1, 1], i.e. we have:

${\displaystyle {\int }_{-1}^1{T}_n(x)T_m(x)\frac{\mathrm{d}x}{\sqrt{1-x^2}}=\{\begin{array}{ll}0& \text{ if }n\ne m,\\ \\ \pi & \text{ if }n=m=0,\\ \\ \frac{\pi }{2}& \text{ if }n=m\ne 0.\end{array}}$

This can be proven by letting x = cos θ and using the defining identity T_n(cos θ) = cos(nθ).

Similarly, the polynomials of the second kind U_n are orthogonal with respect to the weight:

${\displaystyle \sqrt{1-x^2}}$

on the interval [−1, 1], i.e. we have:

${\displaystyle {\int }_{-1}^1{U}_n(x)U_m(x)\sqrt{1-x^2}\mathrm{d}x=\{\begin{array}{ll}0& \text{ if }n\ne m,\\ \frac{\pi }{2}& \text{ if }n=m.\end{array}}$

(The measure √1 − x² dx is, to within a normalizing constant, the Wigner semicircle distribution.)

These orthogonality properties follow from the fact that the Chebyshev polynomials solve the Chebyshev differential equations:

${\displaystyle (1-x^2)T_n^{″}-x{T}_n^{\prime }+n^2{T}_n=0,}$

${\displaystyle (1-x^2)U_n^{″}-3x{U}_n^{\prime }+n(n+2)U_n=0,}$

which are Sturm–Liouville differential equations. It is a general feature of such differential equations that there is a distinguished orthonormal set of solutions. (Another way to define the Chebyshev polynomials is as the solutions to those equations.)

The T_n also satisfy a discrete orthogonality condition:

${\displaystyle \sum _{k=0}^{N-1}{T}_i(x_k)T_j(x_k)=\{\begin{array}{ll}0& \text{ if }i\ne j,\\ N& \text{ if }i=j=0,\\ \frac{N}{2}& \text{ if }i=j\ne 0,\end{array}}$

where N is any integer greater than max(i, j),^[9] and the x_k are the N Chebyshev nodes (see above) of T_N(x):

${\displaystyle x_k=\cos \left(\pi \frac{2k+1}{2N}\right)\text{ for }k=0,1,\dots ,N-1.}$

For the polynomials of the second kind and any integer N > i + j with the same Chebyshev nodes x_k, there are similar sums:

${\displaystyle \sum _{k=0}^{N-1}{U}_i(x_k)U_j(x_k)(1-x_k^2)=\{\begin{array}{ll}0& \text{ if }i\ne j,\\ \frac{N}{2}& \text{ if }i=j,\end{array}}$

and without the weight function:

${\displaystyle \sum _{k=0}^{N-1}{U}_i(x_k)U_j(x_k)=\{\begin{array}{ll}0& \text{ if }i\not\equiv j(\mathrm{mod}2),\\ N\cdot (1+min\{i,j\})& \text{ if }i\equiv j(\mathrm{mod}2).\end{array}}$

For any integer N > i + j, based on the N zeros of U_N(x):

${\displaystyle y_k=\cos \left(\pi \frac{k+1}{N+1}\right)\text{ for }k=0,1,\dots ,N-1,}$

one can get the sum:

${\displaystyle \sum _{k=0}^{N-1}{U}_i(y_k)U_j(y_k)(1-y_k^2)=\{\begin{array}{ll}0& \text{ if }i\ne j,\\ \frac{N+1}{2}& \text{ if }i=j,\end{array}}$

and again without the weight function:

${\displaystyle \sum _{k=0}^{N-1}{U}_i(y_k)U_j(y_k)=\{\begin{array}{ll}0& \text{ if }i\not\equiv j(\mathrm{mod}2),\\ (min\{i,j\}+1)(N-max\{i,j\})& \text{ if }i\equiv j(\mathrm{mod}2).\end{array}}$

Minimal ∞-norm

For any given n ≥ 1, among the polynomials of degree n with leading coefficient 1 (monic polynomials):

${\displaystyle f(x)=\frac{1}{2^{n-1}}{T}_n(x)}$

is the one of which the maximal absolute value on the interval [−1, 1] is minimal.

This maximal absolute value is:

${\displaystyle \frac{1}{2^{n-1}}}$

and |f(x)| reaches this maximum exactly n + 1 times at:

${\displaystyle x=\cos \frac{k\pi }{n}\text{for }0\le k\le n.}$

Remark

By the equioscillation theorem, among all the polynomials of degree ≤ n, the polynomial f minimizes || f ||_∞ on [−1, 1] if and only if there are n + 2 points −1 ≤ x₀ < x₁ < ⋯ < x_{n + 1} ≤ 1 such that | f(x_i)| = || f ||_∞.

Of course, the null polynomial on the interval [−1, 1] can be approximated by itself and minimizes the ∞-norm.

Above, however, | f | reaches its maximum only n + 1 times because we are searching for the best polynomial of degree n ≥ 1 (therefore the theorem evoked previously cannot be used).

Chebyshev polynomials as special cases of more general polynomial families

The Chebyshev polynomials are a special case of the ultraspherical or Gegenbauer polynomials ${\displaystyle C_n^{(\lambda )}(x)}$, which themselves are a special case of the Jacobi polynomials ${\displaystyle P_n^{(\alpha ,\beta )}(x)}$:

${\displaystyle \begin{array}{rl}{T}_n(x)& =\frac{n}{2}\underset{q\to 0}{lim}\frac{1}{q}{C}_n^{(q)}(x)\text{ if }n\ge 1,\\ & =\frac{1}{(\genfrac{}{}{0ex}{}{n-\frac{1}{2}}{n})}{P}_n^{(-\frac{1}{2},-\frac{1}{2})}(x)=\frac{2^{2n}}{(\genfrac{}{}{0ex}{}{2n}{n})}{P}_n^{(-\frac{1}{2},-\frac{1}{2})}(x),\\ U_n(x)& =C_n^{(1)}(x)\\ & =\frac{n+1}{(\genfrac{}{}{0ex}{}{n+\frac{1}{2}}{n})}{P}_n^{(\frac{1}{2},\frac{1}{2})}(x)=\frac{2^{2n+1}}{(\genfrac{}{}{0ex}{}{2n+2}{n+1})}{P}_n^{(\frac{1}{2},\frac{1}{2})}(x).\end{array}}$

Chebyshev polynomials are also a special case of Dickson polynomials:

${\displaystyle D_n(2x\alpha ,{\alpha }^2)=2{\alpha }^n{T}_n(x)}$

${\displaystyle E_n(2x\alpha ,{\alpha }^2)={\alpha }^n{U}_n(x).}$

In particular, when ${\displaystyle \alpha =\frac{1}{2}}$, they are related by ${\displaystyle D_n(x,\frac{1}{4})=2^{1-n}{T}_n(x)}$ and ${\displaystyle E_n(x,\frac{1}{4})=2^{-n}{U}_n(x)}$.

Other properties

The curves given by y = T_n(x), or equivalently, by the parametric equations y = T_n(cos θ) = cos nθ, x = cos θ, are a special case of Lissajous curves with frequency ratio equal to n.

Similar to the formula:

${\displaystyle T_n(\cos \theta )=\cos (n\theta ),}$

we have the analogous formula:

${\displaystyle T_{2n+1}(\sin \theta )=(-1{)}^n\sin \left((2n+1)\theta \right).}$

For x ≠ 0:

${\displaystyle T_n\left(\frac{x+x^{-1}}{2}\right)=\frac{x^n+x^{-n}}{2}}$

and:

${\displaystyle x^n=T_n\left(\frac{x+x^{-1}}{2}\right)+\frac{x-x^{-1}}{2}{U}_{n-1}\left(\frac{x+x^{-1}}{2}\right),}$

which follows from the fact that this holds by definition for x = e^iθ.

Examples

First kind

The first few Chebyshev polynomials of the first kind are OEIS: A028297

${\displaystyle \begin{array}{rl}{T}_0(x)& =1\\ T_1(x)& =x\\ T_2(x)& =2x^2-1\\ T_3(x)& =4x^3-3x\\ T_4(x)& =8x^4-8x^2+1\\ T_5(x)& =16x^5-20x^3+5x\\ T_6(x)& =32x^6-48x^4+18x^2-1\\ T_7(x)& =64x^7-112x^5+56x^3-7x\\ T_8(x)& =128x^8-256x^6+160x^4-32x^2+1\\ T_9(x)& =256x^9-576x^7+432x^5-120x^3+9x\\ T_{10}(x)& =512x^{10}-1280x^8+1120x^6-400x^4+50x^2-1\\ T_{11}(x)& =1024x^{11}-2816x^9+2816x^7-1232x^5+220x^3-11x\end{array}}$

Second kind

The first few Chebyshev polynomials of the second kind are OEIS: A053117

${\displaystyle \begin{array}{rl}{U}_0(x)& =1\\ U_1(x)& =2x\\ U_2(x)& =4x^2-1\\ U_3(x)& =8x^3-4x\\ U_4(x)& =16x^4-12x^2+1\\ U_5(x)& =32x^5-32x^3+6x\\ U_6(x)& =64x^6-80x^4+24x^2-1\\ U_7(x)& =128x^7-192x^5+80x^3-8x\\ U_8(x)& =256x^8-448x^6+240x^4-40x^2+1\\ U_9(x)& =512x^9-1024x^7+672x^5-160x^3+10x\end{array}}$

As a basis set

In the appropriate Sobolev space, the set of Chebyshev polynomials form an orthonormal basis, so that a function in the same space can, on −1 ≤ x ≤ 1, be expressed via the expansion:^[16]

${\displaystyle f(x)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{T}_n(x).}$

Furthermore, as mentioned previously, the Chebyshev polynomials form an orthogonal basis which (among other things) implies that the coefficients a_n can be determined easily through the application of an inner product. This sum is called a Chebyshev series or a Chebyshev expansion.

Since a Chebyshev series is related to a Fourier cosine series through a change of variables, all of the theorems, identities, etc. that apply to Fourier series have a Chebyshev counterpart.^[16] These attributes include:

• The Chebyshev polynomials form a complete orthogonal system.
• The Chebyshev series converges to f(x) if the function is piecewise smooth and continuous. The smoothness requirement can be relaxed in most cases – as long as there are a finite number of discontinuities in f(x) and its derivatives.
• At a discontinuity, the series will converge to the average of the right and left limits.

The abundance of the theorems and identities inherited from Fourier series make the Chebyshev polynomials important tools in numeric analysis; for example they are the most popular general purpose basis functions used in the spectral method,^[16] often in favor of trigonometric series due to generally faster convergence for continuous functions (Gibbs' phenomenon is still a problem).

Example 1

Consider the Chebyshev expansion of log(1 + x). One can express:

${\displaystyle \log (1+x)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{T}_n(x).}$

One can find the coefficients a_n either through the application of an inner product or by the discrete orthogonality condition. For the inner product:

${\displaystyle {\int }_{-1}^{+1}\frac{T_m(x)\log (1+x)}{\sqrt{1-x^2}}\mathrm{d}x=\sum _{n=0}^{\mathrm{\infty }}{a}_n{\int }_{-1}^{+1}\frac{T_m(x)T_n(x)}{\sqrt{1-x^2}}\mathrm{d}x,}$

which gives:

${\displaystyle a_n=\{\begin{array}{ll}-\log 2& \text{ for }n=0,\\ \frac{-2(-1{)}^n}{n}& \text{ for }n>0.\end{array}}$

Alternatively, when the inner product of the function being approximated cannot be evaluated, the discrete orthogonality condition gives an often useful result for approximate coefficients:

${\displaystyle a_n\approx \frac{2-{\delta }_{0n}}{N}\sum _{k=0}^{N-1}{T}_n(x_k)\log (1+x_k),}$

where δ_ij is the Kronecker delta function and the x_k are the N Gauss–Chebyshev zeros of T_N(x):

${\displaystyle x_k=\cos \left(\frac{\pi (k+\frac{1}{2})}{N}\right).}$

For any N, these approximate coefficients provide an exact approximation to the function at x_k with a controlled error between those points. The exact coefficients are obtained with N = ∞, thus representing the function exactly at all points in [−1,1]. The rate of convergence depends on the function and its smoothness.

This allows us to compute the approximate coefficients a_n very efficiently through the discrete cosine transform:

${\displaystyle a_n\approx \frac{2-{\delta }_{0n}}{N}\sum _{k=0}^{N-1}\cos \left(\frac{n\pi (k+\frac{1}{2})}{N}\right)\log (1+x_k).}$

Example 2

To provide another example:

${\displaystyle \begin{array}{rl}(1-x^2{)}^{\alpha }& =-\frac{1}{\sqrt{\pi }}\frac{\mathrm{\Gamma }(\frac{1}{2}+\alpha )}{\mathrm{\Gamma }(\alpha +1)}+2^{1-2\alpha }\sum _{n=0}(-1{)}^n(\genfrac{}{}{0ex}{}{2\alpha }{\alpha -n})T_{2n}(x)\\ & =2^{-2\alpha }\sum _{n=0}(-1{)}^n(\genfrac{}{}{0ex}{}{2\alpha +1}{\alpha -n})U_{2n}(x).\end{array}}$

Partial sums

The partial sums of:

${\displaystyle f(x)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{T}_n(x)}$

are very useful in the approximation of various functions and in the solution of differential equations (see spectral method). Two common methods for determining the coefficients a_n are through the use of the inner product as in Galerkin's method and through the use of collocation which is related to interpolation.

As an interpolant, the N coefficients of the (N − 1)st partial sum are usually obtained on the Chebyshev–Gauss–Lobatto^[17] points (or Lobatto grid), which results in minimum error and avoids Runge's phenomenon associated with a uniform grid. This collection of points corresponds to the extrema of the highest order polynomial in the sum, plus the endpoints and is given by:

${\displaystyle x_k=-\cos \left(\frac{k\pi }{N-1}\right);k=0,1,\dots ,N-1.}$

Polynomial in Chebyshev form

An arbitrary polynomial of degree N can be written in terms of the Chebyshev polynomials of the first kind.^[9] Such a polynomial p(x) is of the form:

${\displaystyle p(x)=\sum _{n=0}^N{a}_n{T}_n(x).}$

Polynomials in Chebyshev form can be evaluated using the Clenshaw algorithm.

Families of polynomials related to Chebyshev polynomials

Polynomials denoted ${\displaystyle C_n(x)}$ and ${\displaystyle S_n(x)}$ closely related to Chebyshev polynomials are sometimes used. They are defined by:^[18]

${\displaystyle C_n(x)=2T_n\left(\frac{x}{2}\right),S_n(x)=U_n\left(\frac{x}{2}\right)}$

and satisfy:

${\displaystyle C_n(x)=S_n(x)-S_{n-2}(x).}$

A. F. Horadam called the polynomials ${\displaystyle C_n(x)}$ Vieta–Lucas polynomials and denoted them ${\displaystyle v_n(x)}$. He called the polynomials ${\displaystyle S_n(x)}$ Vieta–Fibonacci polynomials and denoted them ${\displaystyle V_n(x)}$.^[19] Lists of both sets of polynomials are given in Viète's Opera Mathematica, Chapter IX, Theorems VI and VII.^[20] The Vieta–Lucas and Vieta–Fibonacci polynomials of real argument are, up to a power of ${\displaystyle i}$ and a shift of index in the case of the latter, equal to Lucas and Fibonacci polynomials L_n and F_n of imaginary argument.

Shifted Chebyshev polynomials of the first and second kinds are related to the Chebyshev polynomials by:^[18]

${\displaystyle T_n^{\ast }(x)=T_n(2x-1),U_n^{\ast }(x)=U_n(2x-1).}$

When the argument of the Chebyshev polynomial satisfies 2x − 1 ∈ [−1, 1] the argument of the shifted Chebyshev polynomial satisfies x ∈ [0, 1]. Similarly, one can define shifted polynomials for generic intervals [a, b].

Around 1990 the terms "third-kind" and "fourth-kind" came into use in connection with Chebyshev polynomials, although the polynomials denoted by these terms had an earlier development under the name airfoil polynomials. According to J. C. Mason and G. H. Elliott, the terminology "third-kind" and "fourth-kind" is due to Walter Gautschi, "in consultation with colleagues in the field of orthogonal polynomials."^[21] The Chebyshev polynomials of the third kind are defined as:

${\displaystyle V_n(x)=\frac{\cos \left((n+\frac{1}{2})\theta \right)}{\cos \left(\frac{\theta }{2}\right)}=\sqrt{\frac{2}{1+x}}{T}_{2n+1}\left(\sqrt{\frac{x+1}{2}}\right)}$

and the Chebyshev polynomials of the fourth kind are defined as:

${\displaystyle W_n(x)=\frac{\sin \left((n+\frac{1}{2})\theta \right)}{\sin \left(\frac{\theta }{2}\right)}=U_{2n}\left(\sqrt{\frac{x+1}{2}}\right),}$

where ${\displaystyle \theta =\arccos x}$.^[21][22] In the airfoil literature ${\displaystyle V_n(x)}$ and ${\displaystyle W_n(x)}$ are denoted ${\displaystyle t_n(x)}$ and ${\displaystyle u_n(x)}$. The polynomial families ${\displaystyle T_n(x)}$, ${\displaystyle U_n(x)}$, ${\displaystyle V_n(x)}$, and ${\displaystyle W_n(x)}$ are orthogonal with respect to the weights:

${\displaystyle {(1-x^2)}^{-1/2},{(1-x^2)}^{1/2},(1-x{)}^{-1/2}(1+x{)}^{1/2},(1+x{)}^{-1/2}(1-x{)}^{1/2}}$

and are proportional to Jacobi polynomials ${\displaystyle P_n^{(\alpha ,\beta )}(x)}$ with:

${\displaystyle (\alpha ,\beta )=(-\frac{1}{2},-\frac{1}{2}),(\alpha ,\beta )=(\frac{1}{2},\frac{1}{2}),(\alpha ,\beta )=(-\frac{1}{2},\frac{1}{2}),(\alpha ,\beta )=(\frac{1}{2},-\frac{1}{2}).}$^[22]

All four families satisfy the recurrence ${\displaystyle p_n(x)=2x{p}_{n-1}(x)-p_{n-2}(x)}$ with ${\displaystyle p_0(x)=1}$, where ${\displaystyle p_n=T_n}$, ${\displaystyle U_n}$, ${\displaystyle V_n}$, or ${\displaystyle W_n}$, but they differ according to whether ${\displaystyle p_1(x)}$ equals ${\displaystyle x}$, ${\displaystyle 2x}$, ${\displaystyle 2x-1}$, or ${\displaystyle 2x+1}$.^[21]

See also

• Chebyshev filter
• Chebyshev cube root
• Dickson polynomials
• Legendre polynomials
• Laguerre polynomials
• Hermite polynomials
• Minimal polynomial of 2cos(2pi/n)
• Romanovski polynomials
• Chebyshev rational functions
• Approximation theory
• The Chebfun system
• Discrete Chebyshev transform
• Markov brothers' inequality
• Clenshaw algorithm

References

Sources

• Abramowitz, Milton; Stegun, Irene Ann, eds (1983). "Chapter 22". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. pp. 773. LCCN 65-12253. ISBN 978-0-486-61272-0. http://www.math.sfu.ca/~cbm/aands/page_773.htm. 
• Dette, Holger (1995). "A note on some peculiar nonlinear extremal phenomena of the Chebyshev polynomials". Proceedings of the Edinburgh Mathematical Society 38 (2): 343–355. doi:10.1017/S001309150001912X. 
• Elliott, David (1964). "The evaluation and estimation of the coefficients in the Chebyshev Series expansion of a function". Math. Comp. 18 (86): 274–284. doi:10.1090/S0025-5718-1964-0166903-7. 
• Eremenko, A.; Lempert, L. (1994). "An Extremal Problem For Polynomials". Proceedings of the American Mathematical Society 122 (1): 191–193. doi:10.1090/S0002-9939-1994-1207536-1. http://www.math.purdue.edu/~eremenko/dvi/lempert.pdf. 
• Hernandez, M. A. (2001). "Chebyshev's approximation algorithms and applications". Computers & Mathematics with Applications 41 (3–4): 433–445. doi:10.1016/s0898-1221(00)00286-8. 
• Mason, J. C. (1984). "Some properties and applications of Chebyshev polynomial and rational approximation". Rational Approximation and Interpolation. Lecture Notes in Mathematics. 1105. pp. 27–48. doi:10.1007/BFb0072398. ISBN 978-3-540-13899-0. 
• Mason, J. C.; Handscomb, D.C. (2002). Chebyshev Polynomials. Chapman and Hall/CRC. doi:10.1201/9781420036114. ISBN 978-1-4200-3611-4. https://books.google.com/books?id=8FHf0P3to0UC. 

• Mathar, Richard J. (2006). "Chebyshev series expansion of inverse polynomials". Journal of Computational and Applied Mathematics 196 (2): 596–607. doi:10.1016/j.cam.2005.10.013. Bibcode: 2006JCoAM.196..596M. 
• Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Orthogonal Polynomials", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, http://dlmf.nist.gov/18 
• Remes, Eugene. "On an Extremal Property of Chebyshev Polynomials". https://www.math.technion.ac.il/hat/fpapers/remeztrans.pdf. 
• Salzer, Herbert E. (1976). "Converting interpolation series into Chebyshev series by recurrence formulas". Mathematics of Computation 30 (134): 295–302. doi:10.1090/S0025-5718-1976-0395159-3. 
• Scraton, R.E. (1969). "The Solution of integral equations in Chebyshev series". Mathematics of Computation 23 (108): 837–844. doi:10.1090/S0025-5718-1969-0260224-4. 
• Smith, Lyle B. (1966). "Computation of Chebyshev series coefficients". Comm. ACM 9 (2): 86–87. doi:10.1145/365170.365195. Algorithm 277. 
• Hazewinkel, Michiel, ed. (2001), "Chebyshev polynomials", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Main_Page 

External links

• Weisstein, Eric W.. "Chebyshev polynomial[s of the first kind"]. http://mathworld.wolfram.com/ChebyshevPolynomialoftheFirstKind.html. 
• Mathews, John H. (2003). "Module for Chebyshev polynomials". California State University. http://math.fullerton.edu/mathews/n2003/ChebyshevPolyMod.html. 
• "Chebyshev interpolation: An interactive tour". Mathematical Association of America (MAA). http://www.maa.org/sites/default/files/images/upload_library/4/vol6/Sarra/Chebyshev.htmlnone  – includes illustrative Java applet.
• "Numerical computing with functions". http://www.chebfun.org. 
• "Is there an intuitive explanation for an extremal property of Chebyshev polynomials?". https://mathoverflow.net/q/25534. 
• "Chebyshev polynomial evaluation and the Chebyshev transform". https://www.boost.org/doc/libs/release/libs/math/doc/html/math_toolkit/sf_poly/chebyshev.html. 

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Chebyshev polynomials. Read more