Table of Contents Categories
  Encyclosphere.org ENCYCLOREADER
  supported by EncyclosphereKSF

Computational chemistry

Topic: Chemistry

 From HandWiki - Reading time: 30 min
Short description: Branch of chemistry

Computational chemistry is a branch of chemistry that uses computer simulations to assist in solving chemical problems.[1] It uses methods of theoretical chemistry incorporated into computer programs to calculate the structures and properties of molecules, groups of molecules, and solids.[2] The importance of this subject stems from the fact that, with the exception of some relatively recent findings related to the hydrogen molecular ion (dihydrogen cation), achieving an accurate quantum mechanical depiction of chemical systems analytically, or in a closed form, is not feasible.[3] The complexity inherent in the many-body problem exacerbates the challenge of providing detailed descriptions of quantum mechanical systems.[4] While computational results normally complement information obtained by chemical experiments, it can occasionally predict unobserved chemical phenomena.[5]

A dichromium metal complex with electrostatic field surrounding it. Modelled using WebMO.[6]

Overview

Computational chemistry differs from theoretical chemistry, which involves a mathematical description of chemistry. However, computation chemistry involves the usage of computer programs and additional mathematical skills in order to accurately model various chemical problems. In theoretical chemistry, chemists, physicists, and mathematicians develop algorithms and computer programs to predict atomic and molecular properties and reaction paths for chemical reactions. Computational chemists, in contrast, may simply apply existing computer programs and methodologies to specific chemical questions.[7]

Historically, computational chemistry has had two different aspects:

  • Computational studies, used to find a starting point for a laboratory synthesis or to assist in understanding experimental data, such as the position and source of spectroscopic peaks.[8]
  • Computational studies, used to predict the possibility of so far entirely unknown molecules or to explore reaction mechanisms not readily studied via experiments.[8]

These aspects, along with computational chemistry's purpose, have resulted in a whole host of algorithms.

History

Building on the founding discoveries and theories in the history of quantum mechanics, the first theoretical calculations in chemistry were those of Walter Heitler and Fritz London in 1927, using valence bond theory.[9] The books that were influential in the early development of computational quantum chemistry include Linus Pauling and E. Bright Wilson's 1935 Introduction to Quantum Mechanics – with Applications to Chemistry,[10] Eyring, Walter and Kimball's 1944 Quantum Chemistry,[11] Heitler's 1945 Elementary Wave Mechanics – with Applications to Quantum Chemistry,[12] and later Coulson's 1952 textbook Valence, each of which served as primary references for chemists in the decades to follow.[13]

With the development of efficient computer technology in the 1940s, the solutions of elaborate wave equations for complex atomic systems began to be a realizable objective. In the early 1950s, the first semi-empirical atomic orbital calculations were performed. Theoretical chemists became extensive users of the early digital computers. One significant advancement was marked by Clemens C. J. Roothaan's 1951 paper in the Reviews of Modern Physics.[14][15] This paper focused largely on the "LCAO MO" approach (Linear Combination of Atomic Orbitals Molecular Orbitals). For many years, it was the second-most cited paper in that journal.[14][15] A very detailed account of such use in the United Kingdom is given by Smith and Sutcliffe.[16] The first ab initio Hartree–Fock method calculations on diatomic molecules were performed in 1956 at MIT, using a basis set of Slater orbitals.[17] For diatomic molecules, a systematic study using a minimum basis set and the first calculation with a larger basis set were published by Ransil and Nesbet respectively in 1960.[18] The first polyatomic calculations using Gaussian orbitals were performed in the late 1950s. The first configuration interaction calculations were performed in Cambridge on the EDSAC computer in the 1950s using Gaussian orbitals by Boys and coworkers.[19] By 1971, when a bibliography of ab initio calculations was published,[20] the largest molecules included were naphthalene and azulene.[21][22] Abstracts of many earlier developments in ab initio theory have been published by Schaefer.[23]

In 1964, Hückel method calculations (using a simple linear combination of atomic orbitals (LCAO) method to determine electron energies of molecular orbitals of π electrons in conjugated hydrocarbon systems) of molecules, ranging in complexity from butadiene and benzene to ovalene, were generated on computers at Berkeley and Oxford.[24] These empirical methods were replaced in the 1960s by semi-empirical methods such as CNDO.[25]

In the early 1970s, efficient ab initio computer programs such as ATMOL, Gaussian, IBMOL, and POLYAYTOM, began to be used to speed ab initio calculations of molecular orbitals.[26] Of these four programs, only Gaussian, now vastly expanded, is still in use, but many other programs are now in use.[26] At the same time, the methods of molecular mechanics, such as MM2 force field, were developed, primarily by Norman Allinger.[27]

One of the first mentions of the term computational chemistry can be found in the 1970 book Computers and Their Role in the Physical Sciences by Sidney Fernbach and Abraham Haskell Taub, where they state "It seems, therefore, that 'computational chemistry' can finally be more and more of a reality."[28] During the 1970s, widely different methods began to be seen as part of a new emerging discipline of computational chemistry.[29] The Journal of Computational Chemistry was first published in 1980.

Computational chemistry has featured in several Nobel Prize awards, most notably in 1998 and 2013. Walter Kohn, "for his development of the density-functional theory", and John Pople, "for his development of computational methods in quantum chemistry", received the 1998 Nobel Prize in Chemistry.[30] Martin Karplus, Michael Levitt and Arieh Warshel received the 2013 Nobel Prize in Chemistry for "the development of multiscale models for complex chemical systems".[31]

Applications

There are several fields within computational chemistry.

  • The prediction of the molecular structure of molecules by the use of the simulation of forces, or more accurate quantum chemical methods, to find stationary points on the energy surface as the position of the nuclei is varied.[32]
  • Storing and searching for data on chemical entities (see chemical databases).[33]
  • Identifying correlations between chemical structures and properties (see quantitative structure–property relationship (QSPR) and quantitative structure–activity relationship (QSAR)).[34]
  • Computational approaches to help in the efficient synthesis of compounds.[35]
  • Computational approaches to design molecules that interact in specific ways with other molecules (e.g. drug design and catalysis).[36]

These fields can give rise to several applications as shown below.

Catalysis

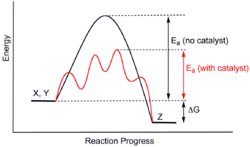
Computational chemistry can help predict values like activation energy from catalysis. The presence of the catalyst opens a different reaction pathway (shown in red) with lower activation energy. The final result and the overall thermodynamics are the same.

Computational chemistry is a tool for analyzing catalytic systems without doing experiments. Modern electronic structure theory and density functional theory has allowed researchers to discover and understand catalysts.[37] Computational studies apply theoretical chemistry to catalysis research. Density functional theory methods calculate the energies and orbitals of molecules to give models of those structures.[38] Using these methods, researchers can predict values like activation energy, site reactivity[39] and other thermodynamic properties.[38]

Data that is difficult to obtain experimentally can be found using computational methods to model the mechanisms of catalytic cycles.[39] Skilled computational chemists provide predictions that are close to experimental data with proper considerations of methods and basis sets. With good computational data, researchers can predict how catalysts can be improved to lower the cost and increase the efficiency of these reactions.[38]

Drug development

Computational chemistry is used in drug development to model potentially useful drug molecules and help companies save time and cost in drug development. The drug discovery process involves analyzing data, finding ways to improve current molecules, finding synthetic routes, and testing those molecules.[36] Computational chemistry helps with this process by giving predictions of which experiments would be best to do without conducting other experiments. Computational methods can also find values that are difficult to find experimentally like pKa's of compounds.[40] Methods like density functional theory can be used to model drug molecules and find their properties, like their HOMO and LUMO energies and molecular orbitals. Computational chemists also help companies with developing informatics, infrastructure and designs of drugs.[41]

Aside from drug synthesis, drug carriers are also researched by computational chemists for nanomaterials. It allows researchers to simulate environments to test the effectiveness and stability of drug carriers. Understanding how water interacts with these nanomaterials ensures stability of the material in human bodies. These computational simulations help researchers optimize the material find the best way to structure these nanomaterials before making them.[42]

Computational chemistry databases

Databases are useful for both computational and non computational chemists in research and verifying the validity of computational methods. Empirical data is used to analyze the error of computational methods against experimental data. Empirical data helps researchers with their methods and basis sets to have greater confidence in the researchers results. Computational chemistry databases are also used in testing software or hardware for computational chemistry.[43]

Databases can also use purely calculated data. Purely calculated data uses calculated values over experimental values for databases. Purely calculated data avoids dealing with these adjusting for different experimental conditions like zero-point energy. These calculations can also avoid experimental errors for difficult to test molecules. Though purely calculated data is often not perfect, identifying issues is often easier for calculated data than experimental.[43]

Databases also give public access to information for researchers to use. They contain data that other researchers have found and uploaded to these databases so that anyone can search for them. Researchers use these databases to find information on molecules of interest and learn what can be done with those molecules. Some publicly available chemistry databases include the following.[43]

  • BindingDB: Contains experimental information about protein-small molecule interactions.[44]
  • RCSB: Stores publicly available 3D models of macromolecules (proteins, nucleic acids) and small molecules (drugs, inhibitors)[45]
  • ChEMBL: Contains data from research on drug development such as assay results.[43]
  • DrugBank: Data about mechanisms of drugs can be found here.[43]

Methods

Ab initio method

The programs used in computational chemistry are based on many different quantum-chemical methods that solve the molecular Schrödinger equation associated with the molecular Hamiltonian.[46] Methods that do not include any empirical or semi-empirical parameters in their equations – being derived directly from theory, with no inclusion of experimental data – are called ab initio methods.[47] A theoretical approximation is rigorously defined on first principles and then solved within an error margin that is qualitatively known beforehand. If numerical iterative methods must be used, the aim is to iterate until full machine accuracy is obtained (the best that is possible with a finite word length on the computer, and within the mathematical and/or physical approximations made).[48]

Ab initio methods need to define a level of theory (the method) and a basis set.[49] A basis set consists of functions centered on the molecule's atoms. These sets are then used to describe molecular orbitals via the linear combination of atomic orbitals (LCAO) molecular orbital method ansatz.[50]

Diagram illustrating various ab initio electronic structure methods in terms of energy. Spacings are not to scale.

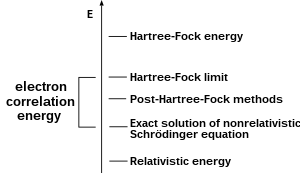
A common type of ab initio electronic structure calculation is the Hartree–Fock method (HF), an extension of molecular orbital theory, where electron-electron repulsions in the molecule are not specifically taken into account; only the electrons' average effect is included in the calculation. As the basis set size increases, the energy and wave function tend towards a limit called the Hartree–Fock limit.[50]

Many types of calculations begin with a Hartree–Fock calculation and subsequently correct for electron-electron repulsion, referred to also as electronic correlation.[51] These types of calculations are termed post-Hartree–Fock methods. By continually improving these methods, scientists can get increasingly closer to perfectly predicting the behavior of atomic and molecular systems under the framework of quantum mechanics, as defined by the Schrödinger equation.[52] To obtain exact agreement with the experiment, it is necessary to include specific terms, some of which are far more important for heavy atoms than lighter ones.[53]

In most cases, the Hartree–Fock wave function occupies a single configuration or determinant.[54] In some cases, particularly for bond-breaking processes, this is inadequate, and several configurations must be used.[55]

The total molecular energy can be evaluated as a function of the molecular geometry; in other words, the potential energy surface.[56] Such a surface can be used for reaction dynamics. The stationary points of the surface lead to predictions of different isomers and the transition structures for conversion between isomers, but these can be determined without full knowledge of the complete surface.[53]

Molecular orbital diagram of the conjugated pi systems of the diazomethane molecule using Hartree-Fock Method, CH2N2

Computational thermochemistry

Main pages: Physics:Computational chemical methods in solid-state physics and Chemistry:Thermochemistry

A particularly important objective, called computational thermochemistry, is to calculate thermochemical quantities such as the enthalpy of formation to chemical accuracy. Chemical accuracy is the accuracy required to make realistic chemical predictions and is generally considered to be 1 kcal/mol or 4 kJ/mol. To reach that accuracy in an economic way, it is necessary to use a series of post-Hartree–Fock methods and combine the results. These methods are called quantum chemistry composite methods.[57]

Chemical dynamics

After the electronic and nuclear variables are separated within the Born–Oppenheimer representation), the wave packet corresponding to the nuclear degrees of freedom is propagated via the time evolution operator (physics) associated to the time-dependent Schrödinger equation (for the full molecular Hamiltonian).[58] In the complementary energy-dependent approach, the time-independent Schrödinger equation is solved using the scattering theory formalism. The potential representing the interatomic interaction is given by the potential energy surfaces. In general, the potential energy surfaces are coupled via the vibronic coupling terms.[59]

The most popular methods for propagating the wave packet associated to the molecular geometry are:

Split operator technique

How a computational method solves quantum equations impacts the accuracy and efficiency of the method. The split operator technique is one of these methods for solving differential equations. In computational chemistry, split operator technique reduces computational costs of simulating chemical systems. Computational costs are about how much time it takes for computers to calculate these chemical systems, as it can take days for more complex systems. Quantum systems are difficult and time-consuming to solve for humans. Split operator methods help computers calculate these systems quickly by solving the sub problems in a quantum differential equation. The method does this by separating the differential equation into 2 different equations, like when there are more than two operators. Once solved, the split equations are combined into one equation again to give an easily calculable solution.[62]

This method is used in many fields that require solving differential equations, such as biology. However, the technique comes with a splitting error. For example, with the following solution for a differential equation.[62]

[math]\displaystyle{ e^{h(A+B)} }[/math]

The equation can be split, but the solutions will not be exact, only similar. This is an example of first order splitting.[62]

[math]\displaystyle{ e^{h(A+B)} \approx e^{hA}e^{hB} }[/math]

There are ways to reduce this error, which include taking an average of two split equations.[62]

Another way to increase accuracy is to use higher order splitting. Usually, second order splitting is the most that is done because higher order splitting requires much more time to calculate and is not worth the cost. Higher order methods become too difficult to implement, and are not useful for solving differential equations despite the higher accuracy.[62]

Computational chemists spend much time making systems calculated with split operator technique more accurate while minimizing the computational cost. Calculating methods is a massive challenge for many chemists trying to simulate molecules or chemical environments.[62]

C60 with isosurface of ground-state electron density as calculated with DFT

Density functional methods

Density functional theory (DFT) methods are often considered to be ab initio methods for determining the molecular electronic structure, even though many of the most common functionals use parameters derived from empirical data, or from more complex calculations. In DFT, the total energy is expressed in terms of the total one-electron density rather than the wave function. In this type of calculation, there is an approximate Hamiltonian and an approximate expression for the total electron density. DFT methods can be very accurate for little computational cost. Some methods combine the density functional exchange functional with the Hartree–Fock exchange term and are termed hybrid functional methods.[63]

Semi-empirical methods

Semi-empirical quantum chemistry methods are based on the Hartree–Fock method formalism, but make many approximations and obtain some parameters from empirical data. They were very important in computational chemistry from the 60s to the 90s, especially for treating large molecules where the full Hartree–Fock method without the approximations were too costly. The use of empirical parameters appears to allow some inclusion of correlation effects into the methods.[64]

Primitive semi-empirical methods were designed even before, where the two-electron part of the Hamiltonian is not explicitly included. For π-electron systems, this was the Hückel method proposed by Erich Hückel, and for all valence electron systems, the extended Hückel method proposed by Roald Hoffmann. Sometimes, Hückel methods are referred to as "completely empirical" because they do not derive from a Hamiltonian.[65] Yet, the term "empirical methods", or "empirical force fields" is usually used to describe Molecular Mechanics.[66]

Molecular mechanics potential energy function with continuum solvent

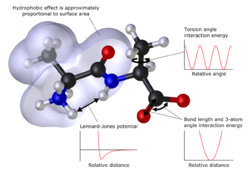
Molecular mechanics

In many cases, large molecular systems can be modeled successfully while avoiding quantum mechanical calculations entirely. Molecular mechanics simulations, for example, use one classical expression for the energy of a compound, for instance, the harmonic oscillator. All constants appearing in the equations must be obtained beforehand from experimental data or ab initio calculations.[64]

The database of compounds used for parameterization, i.e., the resulting set of parameters and functions is called the force field, is crucial to the success of molecular mechanics calculations. A force field parameterized against a specific class of molecules, for instance, proteins, would be expected to only have any relevance when describing other molecules of the same class.[64] These methods can be applied to proteins and other large biological molecules, and allow studies of the approach and interaction (docking) of potential drug molecules.[67][68]File:A molecular dynamics simulation of argon gas.webm

Molecular dynamics

Molecular dynamics (MD) use either quantum mechanics, molecular mechanics or a mixture of both to calculate forces which are then used to solve Newton's laws of motion to examine the time-dependent behavior of systems. The result of a molecular dynamics simulation is a trajectory that describes how the position and velocity of particles varies with time. The phase point of a system described by the positions and momenta of all its particles on a previous time point will determine the next phase point in time by integrating over Newton's laws of motion.[69]

Monte Carlo

Monte Carlo (MC) generates configurations of a system by making random changes to the positions of its particles, together with their orientations and conformations where appropriate.[70] It is a random sampling method, which makes use of the so-called importance sampling. Importance sampling methods are able to generate low energy states, as this enables properties to be calculated accurately. The potential energy of each configuration of the system can be calculated, together with the values of other properties, from the positions of the atoms.[71][72]

Quantum mechanics/molecular mechanics (QM/MM)

QM/MM is a hybrid method that attempts to combine the accuracy of quantum mechanics with the speed of molecular mechanics. It is useful for simulating very large molecules such as enzymes.[73]

Quantum Computational Chemistry

Quantum computational chemistry integrates quantum mechanics and computational methods to simulate chemical systems, distinguishing itself from the QM/MM (Quantum Mechanics/Molecular Mechanics) approach.[74] While QM/MM uses a hybrid approach, combining quantum mechanics for a portion of the system with classical mechanics for the remainder, quantum computational chemistry exclusively uses quantum mechanics to represent and process information, such as Hamiltonian operators.[75]

Conventional computational chemistry methods often struggle with the complex quantum mechanical equations, particularly due to the exponential growth of a quantum system's wave function. Quantum computational chemistry addresses these challenges using quantum computing methods, such as qubitization and quantum phase estimation, which are believed to offer scalable solutions.[76]

Qubitization involves adapting the Hamiltonian operator for more efficient processing on quantum computers, enhancing the simulation's efficiency. Quantum phase estimation, on the other hand, assists in accurately determining energy eigenstates, which are critical for understanding the quantum system's behavior.[77]

While these quantum techniques have advanced the field of computational chemistry, especially in the simulation of chemical systems, their practical application is currently limited mainly to smaller systems due to technological constraints. Nevertheless, these developments represent significant progress towards achieving more precise and resource-efficient quantum chemistry simulations.[76]

Computational costs in chemistry algorithms

Main pages: Computational complexity and List of complexity classes

The computational cost and algorithmic complexity in chemistry are used to help understand and predict chemical phenomena. They help determine which algorithms/computational methods to use when solving chemical problems.This section focuses on the scaling of computational complexity with molecule size and details the algorithms commonly used in both domains.[78]

In quantum chemistry, particularly, the complexity can grow exponentially with the number of electrons involved in the system. This exponential growth is a significant barrier to simulating large or complex systems accurately.[79]

Advanced algorithms in both fields strive to balance accuracy with computational efficiency. For instance, in MD, methods like Verlet integration or Beeman's algorithm are employed for their computational efficiency. In quantum chemistry, hybrid methods combining different computational approaches (like QM/MM) are increasingly used to tackle large biomolecular systems.[80]

Algorithmic complexity examples

The following list illustrates the impact of computational complexity on algorithms used in chemical computations. It is important to note that while this list provides key examples, it is not comprehensive and serves as a guide to understanding how computational demands influence the selection of specific computational methods in chemistry.

Molecular dynamics

Algorithm

Solves Newton's equations of motion for atoms and molecules.[81] File:A Molecular Dynamics Simulation of Liquid Water at 298 K.webm

Complexity

The standard pairwise interaction calculation in MD leads to an [math]\displaystyle{ \mathcal{O}(N^2) }[/math]complexity for [math]\displaystyle{ N }[/math] particles. This is because each particle interacts with every other particle, resulting in [math]\displaystyle{ \frac{N(N-1)}{2} }[/math] interactions.[82] Advanced algorithms, such as the Ewald summation or Fast Multipole Method, reduce this to [math]\displaystyle{ \mathcal{O}(N \log N) }[/math] or even [math]\displaystyle{ \mathcal{O}(N) }[/math] by grouping distant particles and treating them as a single entity or using clever mathematical approximations.[83][84]

Quantum mechanics/molecular mechanics (QM/MM)

Algorithm

Combines quantum mechanical calculations for a small region with molecular mechanics for the larger environment.[85]

Complexity

The complexity of QM/MM methods depends on both the size of the quantum region and the method used for quantum calculations. For example, if a Hartree-Fock method is used for the quantum part, the complexity can be approximated as [math]\displaystyle{ \mathcal{O}(M^2) }[/math], where [math]\displaystyle{ M }[/math] is the number of basis functions in the quantum region. This complexity arises from the need to solve a set of coupled equations iteratively until self-consistency is achieved.[86]

Algorithmic flowchart illustrating the Hartree–Fock method

Hartree-Fock method

Algorithm

Finds a single Fock state that minimizes the energy.[87]

Complexity

NP-hard or NP-complete as demonstrated by embedding instances of the Ising model into Hartree-Fock calculations. The Hartree-Fock method involves solving the Roothaan-Hall equations, which scales as [math]\displaystyle{ \mathcal{O}(N^3) }[/math] to [math]\displaystyle{ \mathcal{O}(N) }[/math] depending on implementation, with [math]\displaystyle{ N }[/math] being the number of basis functions. The computational cost mainly comes from evaluating and transforming the two-electron integrals. This proof of NP-hardness or NP-completeness comes from embedding problems like the Ising model into the Hartree-Fock formalism.[87]

An acrolein molecule. DFT gives good results in the prediction of sensitivity of some nanostructures to environmental pollutants such as Acrolein.[88]

Density functional theory

Algorithm

Investigates the electronic structure or nuclear structure of many-body systems such as atoms, molecules, and the condensed phases.[89]

Complexity

Traditional implementations of DFT typically scale as [math]\displaystyle{ \mathcal{O}(N^3) }[/math], mainly due to the need to diagonalize the Kohn-Sham matrix.[90] The diagonalization step, which finds the eigenvalues and eigenvectors of the matrix, contributes most to this scaling. Recent advances in DFT aim to reduce this complexity through various approximations and algorithmic improvements.[91]

Standard CCSD and CCSD(T) method

Algorithm

CCSD and CCSD(T) methods are advanced electronic structure techniques involving single, double, and in the case of CCSD(T), perturbative triple excitations for calculating electronic correlation effects.[92]

Complexity

CCSD

Scales as [math]\displaystyle{ \mathcal{O}(M^6) }[/math] where [math]\displaystyle{ M }[/math] is the number of basis functions. This intense computational demand arises from the inclusion of single and double excitations in the electron correlation calculation.[92]

CCSD(T)

With the addition of perturbative triples, the complexity increases to [math]\displaystyle{ \mathcal{O}(M^7) }[/math]. This elevated complexity restricts practical usage to smaller systems, typically up to 20-25 atoms in conventional implementations.[92]

Electron density plot of the 2a1 molecular orbital of methane at the CCSD(T)/cc-pVQZ level. Graphic created with Molden based on correlated geometry optimization with CFOUR at the CCSD(T) level in cc-pVQZ basis.

Linear-scaling CCSD(T) method

Algorithm

An adaptation of the standard CCSD(T) method using local natural orbitals (NOs) to significantly reduce the computational burden and enable application to larger systems.[92]

Complexity

Achieves linear scaling with the system size, a major improvement over the traditional fifth-power scaling of CCSD. This advancement allows for practical applications to molecules of up to 100 atoms with reasonable basis sets, marking a significant step forward in computational chemistry's capability to handle larger systems with high accuracy.[92]

Proving the complexity classes for algorithms involves a combination of mathematical proof and computational experiments. For example, in the case of the Hartree-Fock method, the proof of NP-hardness is a theoretical result derived from complexity theory, specifically through reductions from known NP-hard problems.[93]

For other methods like MD or DFT, the computational complexity is often empirically observed and supported by algorithm analysis. In these cases, the proof of correctness is less about formal mathematical proofs and more about consistently observing the computational behaviour across various systems and implementations.[93]

Accuracy

Computational chemistry is not an exact description of real-life chemistry, as the mathematical and physical models of nature can only provide an approximation. However, the majority of chemical phenomena can be described to a certain degree in a qualitative or approximate quantitative computational scheme.[94]

Molecules consist of nuclei and electrons, so the methods of quantum mechanics apply. Computational chemists often attempt to solve the non-relativistic Schrödinger equation, with relativistic corrections added, although some progress has been made in solving the fully relativistic Dirac equation. In principle, it is possible to solve the Schrödinger equation in either its time-dependent or time-independent form, as appropriate for the problem in hand; in practice, this is not possible except for very small systems. Therefore, a great number of approximate methods strive to achieve the best trade-off between accuracy and computational cost.[95]

Accuracy can always be improved with greater computational cost. Significant errors can present themselves in ab initio models comprising many electrons, due to the computational cost of full relativistic-inclusive methods.[92] This complicates the study of molecules interacting with high atomic mass unit atoms, such as transitional metals and their catalytic properties. Present algorithms in computational chemistry can routinely calculate the properties of small molecules that contain up to about 40 electrons with errors for energies less than a few kJ/mol. For geometries, bond lengths can be predicted within a few picometers and bond angles within 0.5 degrees. The treatment of larger molecules that contain a few dozen atoms is computationally tractable by more approximate methods such as density functional theory (DFT).[96]

There is some dispute within the field whether or not the latter methods are sufficient to describe complex chemical reactions, such as those in biochemistry. Large molecules can be studied by semi-empirical approximate methods. Even larger molecules are treated by classical mechanics methods that use what are called molecular mechanics (MM).In QM-MM methods, small parts of large complexes are treated quantum mechanically (QM), and the remainder is treated approximately (MM).[97]

Software packages

Many self-sufficient computational chemistry software packages exist. Some include many methods covering a wide range, while others concentrate on a very specific range or even on one method. Details of most of them can be found in:

Specialized journals on computational chemistry

External links

See also

References

  1. ↑ Parrill, Abby L., ed (2018-10-19) (in en). Reviews in Computational Chemistry, Volume 31 (1 ed.). Wiley. doi:10.1002/series6143. ISBN 978-1-119-51802-0. https://onlinelibrary.wiley.com/doi/book/10.1002/9781119518068. 
  2. ↑ ((National Research Council (US) Committee on Challenges for the Chemical Sciences in the 21st Century)) (2003), "Chemical Theory and Computer Modeling: From Computational Chemistry to Process Systems Engineering" (in en), Beyond the Molecular Frontier: Challenges for Chemistry and Chemical Engineering (National Academies Press (US)), https://www.ncbi.nlm.nih.gov/books/NBK207665/, retrieved 2023-12-05 
  3. ↑ Korobov, Vladimir I.; Karr, J.-Ph. (2021-09-07). "Rovibrational spin-averaged transitions in the hydrogen molecular ions". Physical Review A 104 (3): 032806. doi:10.1103/PhysRevA.104.032806. Bibcode: 2021PhRvA.104c2806K. https://link.aps.org/doi/10.1103/PhysRevA.104.032806. 
  4. ↑ Nozières, Philippe (1997). Theory of interacting Fermi systems. Advanced book classics. Cambridge, Mass: Perseus Publishing. ISBN 978-0-201-32824-0. 
  5. ↑ Willems, Henriëtte; De Cesco, Stephane; Svensson, Fredrik (2020-09-24). "Computational Chemistry on a Budget: Supporting Drug Discovery with Limited Resources: Miniperspective" (in en). Journal of Medicinal Chemistry 63 (18): 10158–10169. doi:10.1021/acs.jmedchem.9b02126. ISSN 0022-2623. PMID 32298123. https://pubs.acs.org/doi/10.1021/acs.jmedchem.9b02126. 
  6. ↑ "WebMO". https://www.webmo.net/. 
  7. ↑ Cramer, Christopher J. (2014). Essentials of computational chemistry: theories and models. Chichester: Wiley. ISBN 978-0-470-09182-1. 
  8. ↑ 8.0 8.1 Patel, Prajay; Melin, Timothé R. L.; North, Sasha C.; Wilson, Angela K. (2021-01-01), Dixon, David A., ed., "Chapter Four - Ab initio composite methodologies: Their significance for the chemistry community", Annual Reports in Computational Chemistry (Elsevier) 17: pp. 113–161, doi:10.1016/bs.arcc.2021.09.002, https://www.sciencedirect.com/science/article/pii/S1574140021000050, retrieved 2023-12-03 
  9. ↑ Heitler, W.; London, F. (1927-06-01). "Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik" (in de). Zeitschrift für Physik 44 (6): 455–472. doi:10.1007/BF01397394. ISSN 0044-3328. Bibcode: 1927ZPhy...44..455H. https://doi.org/10.1007/BF01397394. 
  10. ↑ Pauling, Linus; Wilson, Edgar Bright (1985). Introduction to quantum mechanics: with applications to chemistry. New York: Dover publications. ISBN 978-0-486-64871-2. 
  11. ↑ Eyring, Henry; Walter, John; Kimball, George E. (1967). Quantum chemistry (14th print ed.). New York: Wiley. ISBN 978-0-471-24981-8. 
  12. ↑ Heitler, W. (1956-01-01) (in English). Elementary Wave Mechanics with Applications to Quantum Chemistry (2 ed.). Oxford University Press. ISBN 978-0-19-851103-8. 
  13. ↑ Coulson, Charles Alfred; McWeeny, Roy (1991). Coulson's valence. Oxford science publications (3rd ed.). Oxford New York Toronto [etc.]: Oxford university press. ISBN 978-0-19-855145-4. 
  14. ↑ 14.0 14.1 Roothaan, C. C. J. (1951-04-01). "New Developments in Molecular Orbital Theory". Reviews of Modern Physics 23 (2): 69–89. doi:10.1103/RevModPhys.23.69. Bibcode: 1951RvMP...23...69R. https://link.aps.org/doi/10.1103/RevModPhys.23.69. 
  15. ↑ 15.0 15.1 Ruedenberg, Klaus (1954-11-01). "Free-Electron Network Model for Conjugated Systems. V. Energies and Electron Distributions in the FE MO Model and in the LCAO MO Model". The Journal of Chemical Physics 22 (11): 1878–1894. doi:10.1063/1.1739935. ISSN 0021-9606. Bibcode: 1954JChPh..22.1878R. https://doi.org/10.1063/1.1739935. 
  16. ↑ Smith, S. J.; Sutcliffe, B. T. (1997). "The development of Computational Chemistry in the United Kingdom". Reviews in Computational Chemistry 10: 271–316. 
  17. ↑ Boys, S. F.; Cook, G. B.; Reeves, C. M.; Shavitt, I. (1956-12-01). "Automatic Fundamental Calculations of Molecular Structure" (in en). Nature 178 (4544): 1207–1209. doi:10.1038/1781207a0. ISSN 1476-4687. Bibcode: 1956Natur.178.1207B. https://www.nature.com/articles/1781207a0. 
  18. ↑ Schaefer, Henry F. III (1972). The electronic structure of atoms and molecules. Reading, Massachusetts: Addison-Wesley Publishing Co.. p. 146. https://archive.org/details/electronicstruct0000scha. 
  19. ↑ Boys, S. F.; Cook, G. B.; Reeves, C. M.; Shavitt, I. (1956). "Automatic fundamental calculations of molecular structure". Nature 178 (2): 1207. doi:10.1038/1781207a0. Bibcode: 1956Natur.178.1207B. 
  20. ↑ Richards, W. G.; Walker, T. E. H.; Hinkley R. K. (1971). A bibliography of ab initio molecular wave functions. Oxford: Clarendon Press. 
  21. ↑ Preuss, H. (1968). "DasSCF-MO-P(LCGO)-Verfahren und seine Varianten". International Journal of Quantum Chemistry 2 (5): 651. doi:10.1002/qua.560020506. Bibcode: 1968IJQC....2..651P. 
  22. ↑ Buenker, R. J.; Peyerimhoff, S. D. (1969). "Ab initio SCF calculations for azulene and naphthalene". Chemical Physics Letters 3 (1): 37. doi:10.1016/0009-2614(69)80014-X. Bibcode: 1969CPL.....3...37B. 
  23. ↑ Schaefer, Henry F. III (1984). Quantum Chemistry. Oxford: Clarendon Press. 
  24. ↑ Streitwieser, A.; Brauman, J. I.; Coulson, C. A. (1965). Supplementary Tables of Molecular Orbital Calculations. Oxford: Pergamon Press. 
  25. ↑ Pople, John A.; Beveridge, David L. (1970). Approximate Molecular Orbital Theory. New York: McGraw Hill. 
  26. ↑ 26.0 26.1 Ma, Xiaoyue (2022-12-01). "Development of Computational Chemistry and Application of Computational Methods". Journal of Physics: Conference Series 2386 (1): 012005. doi:10.1088/1742-6596/2386/1/012005. ISSN 1742-6588. Bibcode: 2022JPhCS2386a2005M. https://iopscience.iop.org/article/10.1088/1742-6596/2386/1/012005. 
  27. ↑ Allinger, Norman (1977). "Conformational analysis. 130. MM2. A hydrocarbon force field utilizing V1 and V2 torsional terms". Journal of the American Chemical Society 99 (25): 8127–8134. doi:10.1021/ja00467a001. 
  28. ↑ Fernbach, Sidney; Taub, Abraham Haskell (1970). Computers and Their Role in the Physical Sciences. Routledge. ISBN 978-0-677-14030-8. 
  29. ↑ "vol 1, preface". Reviews in Computational Chemistry. 1. Wiley. 1990. doi:10.1002/9780470125786. ISBN 978-0-470-12578-6. https://onlinelibrary.wiley.com/doi/10.1002/9780470125786.fmatter. 
  30. ↑ "The Nobel Prize in Chemistry 1998". https://www.nobelprize.org/nobel_prizes/chemistry/laureates/1998/index.html. 
  31. ↑ "The Nobel Prize in Chemistry 2013" (Press release). Royal Swedish Academy of Sciences. October 9, 2013. Retrieved October 9, 2013.
  32. ↑ Musil, Felix; Grisafi, Andrea; Bartók, Albert P.; Ortner, Christoph; Csányi, Gábor; Ceriotti, Michele (2021-08-25). "Physics-Inspired Structural Representations for Molecules and Materials" (in en). Chemical Reviews 121 (16): 9759–9815. doi:10.1021/acs.chemrev.1c00021. ISSN 0009-2665. PMID 34310133. 
  33. ↑ Muresan, Sorel; Sitzmann, Markus; Southan, Christopher (2012), Larson, Richard S., ed., "Mapping Between Databases of Compounds and Protein Targets" (in en), Bioinformatics and Drug Discovery, Methods in Molecular Biology (Totowa, NJ: Humana Press) 910: pp. 145–164, doi:10.1007/978-1-61779-965-5_8, ISBN 978-1-61779-965-5, PMID 22821596, PMC 7449375, https://doi.org/10.1007/978-1-61779-965-5_8, retrieved 2023-12-03 
  34. ↑ Roy, Kunal; Kar, Supratik; Das, Rudra Narayan (2015). Understanding the basics of QSAR for applications in pharmaceutical sciences and risk assessment. Amsterdam Boston: Elsevier/Academic Press. ISBN 978-0-12-801505-6. 
  35. ↑ Feng, Fan; Lai, Luhua; Pei, Jianfeng (2018). "Computational Chemical Synthesis Analysis and Pathway Design". Frontiers in Chemistry 6: 199. doi:10.3389/fchem.2018.00199. ISSN 2296-2646. PMID 29915783. 
  36. ↑ 36.0 36.1 Tsui, Vickie; Ortwine, Daniel F.; Blaney, Jeffrey M. (2017-03-01). "Enabling drug discovery project decisions with integrated computational chemistry and informatics" (in en). Journal of Computer-Aided Molecular Design 31 (3): 287–291. doi:10.1007/s10822-016-9988-y. ISSN 1573-4951. PMID 27796615. Bibcode: 2017JCAMD..31..287T. https://doi.org/10.1007/s10822-016-9988-y. 
  37. ↑ Elnabawy, Ahmed O.; Rangarajan, Srinivas; Mavrikakis, Manos (2015-08-01). "Computational chemistry for NH3 synthesis, hydrotreating, and NOx reduction: Three topics of special interest to Haldor Topsøe". Journal of Catalysis. Special Issue: The Impact of Haldor Topsøe on Catalysis 328: 26–35. doi:10.1016/j.jcat.2014.12.018. ISSN 0021-9517. https://www.sciencedirect.com/science/article/pii/S0021951714003534. 
  38. ↑ 38.0 38.1 38.2 Patel, Prajay; Wilson, Angela K. (2020-12-01). "Computational chemistry considerations in catalysis: Regioselectivity and metal-ligand dissociation". Catalysis Today. Proceedings of 3rd International Conference on Catalysis and Chemical Engineering 358: 422–429. doi:10.1016/j.cattod.2020.07.057. ISSN 0920-5861. 
  39. ↑ 39.0 39.1 van Santen, R. A. (1996-05-06). "Computational-chemical advances in heterogeneous catalysis". Journal of Molecular Catalysis A: Chemical. Proceedings of the 8th International Symposium on the Relations between Homogeneous and Heterogeneous Catalysis 107 (1): 5–12. doi:10.1016/1381-1169(95)00161-1. ISSN 1381-1169. https://dx.doi.org/10.1016/1381-1169%2895%2900161-1. 
  40. ↑ van Vlijmen, Herman; Desjarlais, Renee L.; Mirzadegan, Tara (March 2017). "Computational chemistry at Janssen". Journal of Computer-Aided Molecular Design 31 (3): 267–273. doi:10.1007/s10822-016-9998-9. ISSN 1573-4951. PMID 27995515. Bibcode: 2017JCAMD..31..267V. https://pubmed.ncbi.nlm.nih.gov/27995515/. 
  41. ↑ Ahmad, Imad; Kuznetsov, Aleksey E.; Pirzada, Abdul Saboor; Alsharif, Khalaf F.; Daglia, Maria; Khan, Haroon (2023). "Computational pharmacology and computational chemistry of 4-hydroxyisoleucine: Physicochemical, pharmacokinetic, and DFT-based approaches". Frontiers in Chemistry 11. doi:10.3389/fchem.2023.1145974. ISSN 2296-2646. PMID 37123881. Bibcode: 2023FrCh...1145974A. 
  42. ↑ El-Mageed, H. R. Abd; Mustafa, F. M.; Abdel-Latif, Mahmoud K. (2022-01-02). "Boron nitride nanoclusters, nanoparticles and nanotubes as a drug carrier for isoniazid anti-tuberculosis drug, computational chemistry approaches" (in en). Journal of Biomolecular Structure and Dynamics 40 (1): 226–235. doi:10.1080/07391102.2020.1814871. ISSN 0739-1102. PMID 32870128. https://www.tandfonline.com/doi/full/10.1080/07391102.2020.1814871. 
  43. ↑ 43.0 43.1 43.2 43.3 43.4 Muresan, Sorel; Sitzmann, Markus; Southan, Christopher (2012), Larson, Richard S., ed., "Mapping Between Databases of Compounds and Protein Targets" (in en), Bioinformatics and Drug Discovery, Methods in Molecular Biology (Totowa, NJ: Humana Press) 910: pp. 145–164, doi:10.1007/978-1-61779-965-5_8, ISBN 978-1-61779-964-8, PMID 22821596 
  44. ↑ Gilson, Michael K.; Liu, Tiqing; Baitaluk, Michael; Nicola, George; Hwang, Linda; Chong, Jenny (2016-01-04). "BindingDB in 2015: A public database for medicinal chemistry, computational chemistry and systems pharmacology". Nucleic Acids Research 44 (D1): D1045–1053. doi:10.1093/nar/gkv1072. ISSN 1362-4962. PMID 26481362. 
  45. ↑ Zardecki, Christine; Dutta, Shuchismita; Goodsell, David S.; Voigt, Maria; Burley, Stephen K. (2016-03-08). "RCSB Protein Data Bank: A Resource for Chemical, Biochemical, and Structural Explorations of Large and Small Biomolecules" (in en). Journal of Chemical Education 93 (3): 569–575. doi:10.1021/acs.jchemed.5b00404. ISSN 0021-9584. Bibcode: 2016JChEd..93..569Z. 
  46. ↑ "Computational Chemistry and Molecular Modeling" (in en). SpringerLink. 2008. doi:10.1007/978-3-540-77304-7. ISBN 978-3-540-77302-3. https://doi.org/10.1007/978-3-540-77304-7. 
  47. ↑ Leach, Andrew R. (2009). Molecular modelling: principles and applications (2. ed., 12. [Dr.] ed.). Harlow: Pearson/Prentice Hall. ISBN 978-0-582-38210-7. 
  48. ↑ Xu, Peng; Westheimer, Bryce M.; Schlinsog, Megan; Sattasathuchana, Tosaporn; Elliott, George; Gordon, Mark S.; Guidez, Emilie (2024-01-01). "The Effective Fragment Potential: An Ab Initio Force Field" (in en-US). Comprehensive Computational Chemistry: 153–161. doi:10.1016/B978-0-12-821978-2.00141-0. ISBN 9780128232569. https://www.sciencedirect.com/science/article/abs/pii/B9780128219782001410. 
  49. ↑ Friesner, Richard A. (2005-05-10). "Ab initio quantum chemistry: Methodology and applications" (in en). Proceedings of the National Academy of Sciences 102 (19): 6648–6653. doi:10.1073/pnas.0408036102. ISSN 0027-8424. PMID 15870212. 
  50. ↑ 50.0 50.1 Hinchliffe, Alan (2001). Modelling molecular structures. Wiley series in theoretical chemistry (2nd, reprint ed.). Chichester: Wiley. ISBN 978-0-471-48993-1. 
  51. ↑ S, D R Hartree F R (1947-01-01). "The calculation of atomic structures". Reports on Progress in Physics 11 (1): 113–143. doi:10.1088/0034-4885/11/1/305. Bibcode: 1947RPPh...11..113S. https://iopscience.iop.org/article/10.1088/0034-4885/11/1/305. 
  52. ↑ Møller, Chr.; Plesset, M. S. (1934-10-01). "Note on an Approximation Treatment for Many-Electron Systems" (in en). Physical Review 46 (7): 618–622. doi:10.1103/PhysRev.46.618. ISSN 0031-899X. Bibcode: 1934PhRv...46..618M. https://link.aps.org/doi/10.1103/PhysRev.46.618. 
  53. ↑ 53.0 53.1 Matveeva, Regina; Folkestad, Sarai Dery; Høyvik, Ida-Marie (2023-02-09). "Particle-Breaking Hartree–Fock Theory for Open Molecular Systems" (in en). The Journal of Physical Chemistry A (American Chemical Society) 127 (5): 1329–1341. doi:10.1021/acs.jpca.2c07686. ISSN 1089-5639. PMID 36720055. Bibcode: 2023JPCA..127.1329M. 
  54. ↑ McLACHLAN, A. D.; BALL, M. A. (1964-07-01). "Time-Dependent Hartree---Fock Theory for Molecules". Reviews of Modern Physics 36 (3): 844–855. doi:10.1103/RevModPhys.36.844. Bibcode: 1964RvMP...36..844M. https://link.aps.org/doi/10.1103/RevModPhys.36.844. 
  55. ↑ Cohen, Maurice; Kelly, Paul S. (1967-05-01). "HARTREE–FOCK WAVE FUNCTIONS FOR EXCITED STATES: III. DIPOLE TRANSITIONS IN THREE-ELECTRON SYSTEMS" (in en). Canadian Journal of Physics 45 (5): 1661–1673. doi:10.1139/p67-129. ISSN 0008-4204. Bibcode: 1967CaJPh..45.1661C. http://www.nrcresearchpress.com/doi/10.1139/p67-129. 
  56. ↑ Ballard, Andrew J.; Das, Ritankar; Martiniani, Stefano; Mehta, Dhagash; Sagun, Levent; Stevenson, Jacob D.; Wales, David J. (2017-05-24). "Energy landscapes for machine learning" (in en). Physical Chemistry Chemical Physics 19 (20): 12585–12603. doi:10.1039/C7CP01108C. ISSN 1463-9084. PMID 28367548. Bibcode: 2017PCCP...1912585B. https://pubs.rsc.org/en/content/articlelanding/2017/cp/c7cp01108c. 
  57. ↑ Ohlinger, W. S.; Klunzinger, P. E.; Deppmeier, B. J.; Hehre, W. J. (2009-03-12). "Efficient Calculation of Heats of Formation" (in en). The Journal of Physical Chemistry A 113 (10): 2165–2175. doi:10.1021/jp810144q. ISSN 1089-5639. PMID 19222177. https://pubs.acs.org/doi/10.1021/jp810144q. 
  58. ↑ Butler, Laurie J. (October 1998). "Chemical Reaction Dynamics Beyond the Born-Oppenheimer Approximation" (in en). Annual Review of Physical Chemistry 49 (1): 125–171. doi:10.1146/annurev.physchem.49.1.125. ISSN 0066-426X. PMID 15012427. Bibcode: 1998ARPC...49..125B. https://www.annualreviews.org/doi/10.1146/annurev.physchem.49.1.125. 
  59. ↑ Ito, Kenichi; Nakamura, Shu (June 2010). "Time-dependent scattering theory for Schrödinger operators on scattering manifolds" (in en). Journal of the London Mathematical Society 81 (3): 774–792. doi:10.1112/jlms/jdq018. http://doi.wiley.com/10.1112/jlms/jdq018. 
  60. ↑ Ambrose, D; Counsell, J. F; Davenport, A. J (1970-03-01). "The use of Chebyshev polynomials for the representation of vapour pressures between the triple point and the critical point". The Journal of Chemical Thermodynamics 2 (2): 283–294. doi:10.1016/0021-9614(70)90093-5. ISSN 0021-9614. https://dx.doi.org/10.1016/0021-9614%2870%2990093-5. 
  61. ↑ Manthe, U.; Meyer, H.-D.; Cederbaum, L. S. (1992-09-01). "Wave-packet dynamics within the multiconfiguration Hartree framework: General aspects and application to NOCl". The Journal of Chemical Physics 97 (5): 3199–3213. doi:10.1063/1.463007. ISSN 0021-9606. Bibcode: 1992JChPh..97.3199M. https://doi.org/10.1063/1.463007. 
  62. ↑ 62.0 62.1 62.2 62.3 62.4 62.5 62.6 Lukassen, Axel Ariaan; Kiehl, Martin (2018-12-15). "Operator splitting for chemical reaction systems with fast chemistry". Journal of Computational and Applied Mathematics 344: 495–511. doi:10.1016/j.cam.2018.06.001. ISSN 0377-0427. 
  63. ↑ De Proft, Frank; Geerlings, Paul; Heidar-Zadeh, Farnaz; Ayers, Paul W. (2024-01-01). "Conceptual Density Functional Theory" (in en-US). Comprehensive Computational Chemistry: 306–321. doi:10.1016/B978-0-12-821978-2.00025-8. ISBN 9780128232569. https://www.sciencedirect.com/science/article/abs/pii/B9780128219782000258. 
  64. ↑ 64.0 64.1 64.2 Ramachandran, K. I.; Deepa, G.; Namboori, K. (2008). Computational chemistry and molecular modeling: principles and applications. Berlin: Springer. ISBN 978-3-540-77304-7. 
  65. ↑ Counts, Richard W. (1987-07-01). "Strategies I" (in en). Journal of Computer-Aided Molecular Design 1 (2): 177–178. doi:10.1007/bf01676961. ISSN 0920-654X. PMID 3504968. Bibcode: 1987JCAMD...1..177C. 
  66. ↑ Dinur, Uri; Hagler, Arnold T. (1991). Lipkowitz, Kenny B.. ed (in en). Reviews in Computational Chemistry. John Wiley & Sons, Inc.. pp. 99–164. doi:10.1002/9780470125793.ch4. ISBN 978-0-470-12579-3. 
  67. ↑ Rubenstein, Lester A.; Zauhar, Randy J.; Lanzara, Richard G. (2006). "Molecular dynamics of a biophysical model for β2-adrenergic and G protein-coupled receptor activation". Journal of Molecular Graphics and Modelling 25 (4): 396–409. doi:10.1016/j.jmgm.2006.02.008. PMID 16574446. http://www.bio-balance.com/JMGM_article.pdf. 
  68. ↑ Rubenstein, Lester A.; Lanzara, Richard G. (1998). "Activation of G protein-coupled receptors entails cysteine modulation of agonist binding". Journal of Molecular Structure: THEOCHEM 430: 57–71. doi:10.1016/S0166-1280(98)90217-2. http://www.bio-balance.com/GPCR_Activation.pdf. 
  69. ↑ Hutter, Jürg; Iannuzzi, Marcella; Kühne, Thomas D. (2024-01-01). "Ab Initio Molecular Dynamics: A Guide to Applications" (in en-US). Comprehensive Computational Chemistry: 493–517. doi:10.1016/B978-0-12-821978-2.00096-9. ISBN 9780128232569. https://www.sciencedirect.com/science/article/abs/pii/B9780128219782000969. 
  70. ↑ Satoh, A. (2003-01-01), Satoh, A., ed., "Chapter 3 - Monte Carlo Methods", Studies in Interface Science, Introduction to Molecular-Microsimulation of Colloidal Dispersions (Elsevier) 17: pp. 19–63, doi:10.1016/S1383-7303(03)80031-5, ISBN 9780444514240, https://www.sciencedirect.com/science/article/pii/S1383730303800315, retrieved 2023-12-03 
  71. ↑ Allen, M. P. (1987). Computer simulation of liquids. D. J. Tildesley. Oxford [England]: Clarendon Press. ISBN 0-19-855375-7. OCLC 15132676. 
  72. ↑ McArdle, Sam; Endo, Suguru; Aspuru-Guzik, Alán; Benjamin, Simon C.; Yuan, Xiao (2020-03-30). "Quantum computational chemistry" (in en). Reviews of Modern Physics 92 (1): 015003. doi:10.1103/RevModPhys.92.015003. ISSN 0034-6861. Bibcode: 2020RvMP...92a5003M. 
  73. ↑ Bignon, Emmanuelle; Monari, Antonio (2024-01-01). "Molecular Dynamics and QM/MM to Understand Genome Organization and Reproduction in Emerging RNA Viruses" (in en-US). Comprehensive Computational Chemistry: 895–909. doi:10.1016/B978-0-12-821978-2.00101-X. ISBN 9780128232569. https://www.sciencedirect.com/science/article/abs/pii/B978012821978200101X. 
  74. ↑ Abrams, Daniel S.; Lloyd, Seth (1999-12-13). "Quantum Algorithm Providing Exponential Speed Increase for Finding Eigenvalues and Eigenvectors". Physical Review Letters 83 (24): 5162–5165. doi:10.1103/PhysRevLett.83.5162. Bibcode: 1999PhRvL..83.5162A. https://link.aps.org/doi/10.1103/PhysRevLett.83.5162. 
  75. ↑ Feynman, Richard P. (2019-06-17). Feynman Lectures On Computation. Boca Raton: CRC Press. doi:10.1201/9780429500442. ISBN 978-0-429-50044-2. https://www.taylorfrancis.com/books/mono/10.1201/9780429500442/feynman-lectures-computation-richard-feynman. 
  76. ↑ 76.0 76.1 Nielsen, Michael A.; Chuang, Isaac L. (2010). Quantum computation and quantum information (10th anniversary ed.). Cambridge: Cambridge university press. ISBN 978-1-107-00217-3. 
  77. ↑ McArdle, Sam; Endo, Suguru; Aspuru-Guzik, Alán; Benjamin, Simon C.; Yuan, Xiao (2020-03-30). "Quantum computational chemistry". Reviews of Modern Physics 92 (1): 015003. doi:10.1103/RevModPhys.92.015003. Bibcode: 2020RvMP...92a5003M. 
  78. ↑ Jäger, Jonas; Krems, Roman V. (2023-02-02). "Universal expressiveness of variational quantum classifiers and quantum kernels for support vector machines" (in en). Nature Communications (Nature) 14 (1): 576. doi:10.1038/s41467-023-36144-5. ISSN 2041-1723. PMID 36732519. Bibcode: 2023NatCo..14..576J. 
  79. ↑ Modern electronic structure theory. 1. Advanced series in physical chemistry. Singapore: World Scientific. 1995. ISBN 978-981-02-2987-0. 
  80. ↑ Adcock, Stewart A.; McCammon, J. Andrew (2006-05-01). "Molecular Dynamics: Survey of Methods for Simulating the Activity of Proteins" (in en). Chemical Reviews 106 (5): 1589–1615. doi:10.1021/cr040426m. ISSN 0009-2665. PMID 16683746. 
  81. ↑ Durrant, Jacob D.; McCammon, J. Andrew (2011-10-28). "Molecular dynamics simulations and drug discovery". BMC Biology 9 (1): 71. doi:10.1186/1741-7007-9-71. ISSN 1741-7007. PMID 22035460. 
  82. ↑ Stephan, Simon; Horsch, Martin T.; Vrabec, Jadran; Hasse, Hans (2019-07-03). "MolMod – an open access database of force fields for molecular simulations of fluids" (in en). Molecular Simulation 45 (10): 806–814. doi:10.1080/08927022.2019.1601191. ISSN 0892-7022. https://www.tandfonline.com/doi/full/10.1080/08927022.2019.1601191. 
  83. ↑ Kurzak, J.; Pettitt, B. M. (September 2006). "Fast multipole methods for particle dynamics" (in en). Molecular Simulation 32 (10–11): 775–790. doi:10.1080/08927020600991161. ISSN 0892-7022. PMID 19194526. 
  84. ↑ Giese, Timothy J.; Panteva, Maria T.; Chen, Haoyuan; York, Darrin M. (2015-02-10). "Multipolar Ewald Methods, 1: Theory, Accuracy, and Performance" (in en). Journal of Chemical Theory and Computation 11 (2): 436–450. doi:10.1021/ct5007983. ISSN 1549-9618. PMID 25691829. 
  85. ↑ Groenhof, Gerrit (2013), Monticelli, Luca; Salonen, Emppu, eds., "Introduction to QM/MM Simulations" (in en), Biomolecular Simulations: Methods and Protocols, Methods in Molecular Biology (Totowa, NJ: Humana Press) 924: pp. 43–66, doi:10.1007/978-1-62703-017-5_3, ISBN 978-1-62703-017-5, PMID 23034745 
  86. ↑ Tzeliou, Christina Eleftheria; Mermigki, Markella Aliki; Tzeli, Demeter (January 2022). "Review on the QM/MM Methodologies and Their Application to Metalloproteins" (in en). Molecules 27 (9): 2660. doi:10.3390/molecules27092660. ISSN 1420-3049. PMID 35566011. 
  87. ↑ 87.0 87.1 Lucas, Andrew (2014). "Ising formulations of many NP problems". Frontiers in Physics 2: 5. doi:10.3389/fphy.2014.00005. ISSN 2296-424X. Bibcode: 2014FrP.....2....5L. 
  88. ↑ Rastegar, Somayeh F.; Hadipour, Nasser L.; Tabar, Mohammad Bigdeli; Soleymanabadi, Hamed (2013-09-01). "DFT studies of acrolein molecule adsorption on pristine and Al- doped graphenes" (in en). Journal of Molecular Modeling 19 (9): 3733–3740. doi:10.1007/s00894-013-1898-5. ISSN 1610-2940. http://link.springer.com/10.1007/s00894-013-1898-5. 
  89. ↑ Kohn, W.; Sham, L. J. (1965-11-15). "Self-Consistent Equations Including Exchange and Correlation Effects". Physical Review 140 (4A): A1133–A1138. doi:10.1103/PhysRev.140.A1133. Bibcode: 1965PhRv..140.1133K. 
  90. ↑ Michaud-Rioux, Vincent; Zhang, Lei; Guo, Hong (2016-02-15). "RESCU: A real space electronic structure method". Journal of Computational Physics 307: 593–613. doi:10.1016/j.jcp.2015.12.014. ISSN 0021-9991. Bibcode: 2016JCoPh.307..593M. https://www.sciencedirect.com/science/article/pii/S0021999115008335. 
  91. ↑ Motamarri, Phani; Das, Sambit; Rudraraju, Shiva; Ghosh, Krishnendu; Davydov, Denis; Gavini, Vikram (2020-01-01). "DFT-FE – A massively parallel adaptive finite-element code for large-scale density functional theory calculations". Computer Physics Communications 246: 106853. doi:10.1016/j.cpc.2019.07.016. ISSN 0010-4655. Bibcode: 2020CoPhC.24606853M. https://www.sciencedirect.com/science/article/pii/S0010465519302309. 
  92. ↑ 92.0 92.1 92.2 92.3 92.4 92.5 Sengupta, Arkajyoti; Ramabhadran, Raghunath O.; Raghavachari, Krishnan (2016-01-15). "Breaking a bottleneck: Accurate extrapolation to "gold standard" CCSD(T) energies for large open shell organic radicals at reduced computational cost" (in en). Journal of Computational Chemistry 37 (2): 286–295. doi:10.1002/jcc.24050. ISSN 0192-8651. PMID 26280676. https://onlinelibrary.wiley.com/doi/10.1002/jcc.24050. 
  93. ↑ 93.0 93.1 Whitfield, James Daniel; Love, Peter John; Aspuru-Guzik, Alán (2013). "Computational complexity in electronic structure" (in en). Phys. Chem. Chem. Phys. 15 (2): 397–411. doi:10.1039/C2CP42695A. ISSN 1463-9076. PMID 23172634. Bibcode: 2013PCCP...15..397W. http://xlink.rsc.org/?DOI=C2CP42695A. 
  94. ↑ Mathematical Challenges from Theoretical/Computational Chemistry. Washington, D.C.: National Academies Press. 1995-03-29. doi:10.17226/4886. ISBN 978-0-309-05097-5. http://www.nap.edu/catalog/4886. 
  95. ↑ Visscher, Lucas (June 2002). "The Dirac equation in quantum chemistry: Strategies to overcome the current computational problems" (in en). Journal of Computational Chemistry 23 (8): 759–766. doi:10.1002/jcc.10036. ISSN 0192-8651. PMID 12012352. https://onlinelibrary.wiley.com/doi/10.1002/jcc.10036. 
  96. ↑ Sax, Alexander F. (2008-04-01). "Computational Chemistry techniques: covering orders of magnitude in space, time, and accuracy" (in en). Monatshefte für Chemie - Chemical Monthly 139 (4): 299–308. doi:10.1007/s00706-007-0827-7. ISSN 1434-4475. https://doi.org/10.1007/s00706-007-0827-7. 
  97. ↑ Friesner, R. (2003-03-01). "How iron-containing proteins control dioxygen chemistry: a detailed atomic level description via accurate quantum chemical and mixed quantum mechanics/molecular mechanics calculations" (in en-US). Coordination Chemistry Reviews 238-239: 267–290. doi:10.1016/S0010-8545(02)00284-9. ISSN 0010-8545. https://www.sciencedirect.com/science/article/abs/pii/S0010854502002849. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Chemistry:Computational_chemistry&oldid=3420853"
Licensed under CC BY-SA 3.0 | Source: https://handwiki.org/wiki/Chemistry:Computational_chemistry
6 views | Status: cached on July 19 2024 11:53:20
↧ Download this article as ZWI file
Encyclosphere.org EncycloReader is supported by the EncyclosphereKSF