Extended periodic table
Topic: Chemistry
 From HandWiki - Reading time: 59 min
From HandWiki - Reading time: 59 min
| Part of a series on the |
| Periodic table |
|---|
An extended periodic table theorizes about chemical elements beyond those currently known and proven. The element with the highest atomic number known is oganesson (Z = 118), which completes the seventh period (row) in the periodic table. All elements in the eighth period and beyond thus remain purely hypothetical.
Elements beyond 118 would be placed in additional periods when discovered, laid out (as with the existing periods) to illustrate periodically recurring trends in the properties of the elements. Any additional periods are expected to contain more elements than the seventh period, as they are calculated to have an additional so-called g-block, containing at least 18 elements with partially filled g-orbitals in each period. An eight-period table containing this block was suggested by Glenn T. Seaborg in 1969.[1][2] The first element of the g-block may have atomic number 121, and thus would have the systematic name unbiunium. Despite many searches, no elements in this region have been synthesized or discovered in nature.[3]
According to the orbital approximation in quantum mechanical descriptions of atomic structure, the g-block would correspond to elements with partially filled g-orbitals, but spin–orbit coupling effects reduce the validity of the orbital approximation substantially for elements of high atomic number. Seaborg's version of the extended period had the heavier elements following the pattern set by lighter elements, as it did not take into account relativistic effects. Models that take relativistic effects into account predict that the pattern will be broken. Pekka Pyykkö and Burkhard Fricke used computer modeling to calculate the positions of elements up to Z = 172, and found that several were displaced from the Madelung rule.[4] As a result of uncertainty and variability in predictions of chemical and physical properties of elements beyond 120, there is currently no consensus on their placement in the extended periodic table.
Elements in this region are likely to be highly unstable with respect to radioactive decay and undergo alpha decay or spontaneous fission with extremely short half-lives, though element 126 is hypothesized to be within an island of stability that is resistant to fission but not to alpha decay. Other islands of stability beyond the known elements may also be possible, including one theorised around element 164, though the extent of stabilizing effects from closed nuclear shells is uncertain. It is not clear how many elements beyond the expected island of stability are physically possible, whether period 8 is complete, or if there is a period 9. The International Union of Pure and Applied Chemistry (IUPAC) defines an element to exist if its lifetime is longer than 10−14 seconds (0.01 picoseconds, or 10 femtoseconds), which is the time it takes for the nucleus to form an electron cloud.[5]
As early as 1940, it was noted that a simplistic interpretation of the relativistic Dirac equation runs into problems with electron orbitals at Z > 1/α ≈ 137.036 (the reciprocal of the fine-structure constant), suggesting that neutral atoms cannot exist beyond element 137, and that a periodic table of elements based on electron orbitals therefore breaks down at this point.[6] On the other hand, a more rigorous analysis calculates the analogous limit to be Z ≈ 168–172 where the 1s subshell dives into the Dirac sea, and that it is instead not neutral atoms that cannot exist beyond this point, but bare nuclei, thus posing no obstacle to the further extension of the periodic system. Atoms beyond this critical atomic number are called supercritical atoms.
History
Elements beyond the actinides were first proposed to exist as early as 1895, when Danish chemist Hans Peter Jørgen Julius Thomsen predicted that thorium and uranium formed part of a 32-element period which would end at a chemically inactive element with atomic weight 292 (not far from the 294 for the only known isotope of oganesson). In 1913, Swedish physicist Johannes Rydberg similarly predicted that the next noble gas after radon would have atomic number 118, and purely formally derived even heavier congeners of radon at Z = 168, 218, 290, 362, and 460, exactly where the Aufbau principle would predict them to be. In 1922, Niels Bohr predicted the electronic structure of this next noble gas at Z = 118, and suggested that the reason why elements beyond uranium were not seen in nature was because they were too unstable. The German physicist and engineer Richard Swinne published a review paper in 1926 containing predictions on the transuranic elements (he may have coined the term) in which he anticipated modern predictions of an island of stability: he first hypothesised in 1914 that half-lives should not decrease strictly with atomic number, but suggested instead that there might be some longer-lived elements at Z = 98–102 and Z = 108–110, and speculated that such elements might exist in the Earth's core, in iron meteorites, or in the ice caps of Greenland where they had been locked up from their supposed cosmic origin.[7] By 1955, these elements were called superheavy elements.[8]
The first predictions on properties of undiscovered superheavy elements were made in 1957, when the concept of nuclear shells was first explored and an island of stability was theorized to exist around element 126.[9] In 1967, more rigorous calculations were performed, and the island of stability was theorized to be centered at the then-undiscovered flerovium (element 114); this and other subsequent studies motivated many researchers to search for superheavy elements in nature or attempt to synthesize them at accelerators.[8] Many searches for superheavy elements were conducted in the 1970s, all with negative results. As of April 2022[update], synthesis has been attempted for every element up to and including unbiseptium (Z = 127), except unbitrium (Z = 123),[10][11][12] with the heaviest successfully synthesized element being oganesson in 2002 and the most recent discovery being that of tennessine in 2010.[10]
As some superheavy elements were predicted to lie beyond the seven-period periodic table, an additional eighth period containing these elements was first proposed by Glenn T. Seaborg in 1969. This model continued the pattern in established elements and introduced a new g-block and superactinide series beginning at element 121, raising the number of elements in period 8 compared to known periods.[1][2][8] These early calculations failed to consider relativistic effects that break down periodic trends and render simple extrapolation impossible, however. In 1971, Fricke calculated the periodic table up to Z = 172, and discovered that some elements indeed had different properties that break the established pattern,[4] and a 2010 calculation by Pekka Pyykkö also noted that several elements might behave differently than expected.[13] It is unknown how far the periodic table might extend beyond the known 118 elements, as heavier elements are predicted to be increasingly unstable. Glenn T. Seaborg suggested that practically speaking, the end of the periodic table might come as early as around Z = 120 due to nuclear instability.[14]
Predicted structures of an extended periodic table
There is currently no consensus on the placement of elements beyond atomic number 120 in the periodic table.
All hypothetical elements are given an International Union of Pure and Applied Chemistry (IUPAC) systematic element name, for use until the element has been discovered, confirmed, and an official name is approved. These names are typically not used in the literature, and the elements are instead referred to by their atomic numbers; hence, element 164 is usually not called "unhexquadium" or "Uhq" (the systematic name and symbol), but rather "element 164" with symbol "164", "(164)", or "E164".[15]
Aufbau principle
At element 118, the orbitals 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d and 7p are assumed to be filled, with the remaining orbitals unfilled. A simple extrapolation from the Aufbau principle would predict the eighth row to fill orbitals in the order 8s, 5g, 6f, 7d, 8p; but after element 120, the proximity of the electron shells makes placement in a simple table problematic.
| 1 | 1 H |
2 He | ||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 Li |
4 Be |
5 B |
6 C |
7 N |
8 O |
9 F |
10 Ne | ||||||||||||||||||||||||||||||||||||||||||
| 3 | 11 Na |
12 Mg |
13 Al |
14 Si |
15 P |
16 S |
17 Cl |
18 Ar | ||||||||||||||||||||||||||||||||||||||||||
| 4 | 19 K |
20 Ca |
21 Sc |
22 Ti |
23 V |
24 Cr |
25 Mn |
26 Fe |
27 Co |
28 Ni |
29 Cu |
30 Zn |
31 Ga |
32 Ge |
33 As |
34 Se |
35 Br |
36 Kr | ||||||||||||||||||||||||||||||||
| 5 | 37 Rb |
38 Sr |
39 Y |
40 Zr |
41 Nb |
42 Mo |
43 Tc |
44 Ru |
45 Rh |
46 Pd |
47 Ag |
48 Cd |
49 In |
50 Sn |
51 Sb |
52 Te |
53 I |
54 Xe | ||||||||||||||||||||||||||||||||
| 6 | 55 Cs |
56 Ba |
57 La |
58 Ce |
59 Pr |
60 Nd |
61 Pm |
62 Sm |
63 Eu |
64 Gd |
65 Tb |
66 Dy |
67 Ho |
68 Er |
69 Tm |
70 Yb |
71 Lu |
72 Hf |
73 Ta |
74 W |
75 Re |
76 Os |
77 Ir |
78 Pt |
79 Au |
80 Hg |
81 Tl |
82 Pb |
83 Bi |
84 Po |
85 At |
86 Rn | ||||||||||||||||||
| 7 | 87 Fr |
88 Ra |
89 Ac |
90 Th |
91 Pa |
92 U |
93 Np |
94 Pu |
95 Am |
96 Cm |
97 Bk |
98 Cf |
99 Es |
100 Fm |
101 Md |
102 No |
103 Lr |
104 Rf |
105 Db |
106 Sg |
107 Bh |
108 Hs |
109 Mt |
110 Ds |
111 Rg |
112 Cn |
113 Nh |
114 Fl |
115 Mc |
116 Lv |
117 Ts |
118 Og | ||||||||||||||||||
| 8 | 119 Uue |
120 Ubn |
121 Ubu |
122 Ubb |
123 Ubt |
124 Ubq |
125 Ubp |
126 Ubh |
127 Ubs |
128 Ubo |
129 Ube |
130 Utn |
131 Utu |
132 Utb |
133 Utt |
134 Utq |
135 Utp |
136 Uth |
137 Uts |
138 Uto |
139 Ute |
140 Uqn |
141 Uqu |
142 Uqb |
143 Uqt |
144 Uqq |
145 Uqp |
146 Uqh |
147 Uqs |
148 Uqo |
149 Uqe |
150 Upn |
151 Upu |
152 Upb |
153 Upt |
154 Upq |
155 Upp |
156 Uph |
157 Ups |
158 Upo |
159 Upe |
160 Uhn |
161 Uhu |
162 Uhb |
163 Uht |
164 Uhq |
165 Uhp |
166 Uhh |
167 Uhs |
168 Uho |
Background color shows subcategory in the metal–metalloid–nonmetal trend:
| Metal | Metalloid | Nonmetal | Unknown chemical properties | |||||||
| Alkali metal | Alkaline earth metal | Lanthanide | Actinide | Transition metal | Post-transition metal | Transition metal | Transition metal | |||
Fricke
Not all models show the higher elements following the pattern established by lighter elements. Burkhard Fricke et al., who carried out calculations up to element 184 in an article published in 1971, also found some elements to be displaced from the Madelung energy-ordering rule as a result of overlapping orbitals; this is caused by the increasing role of relativistic effects in heavy elements (They describe chemical properties up to element 184, but only draw a table to element 172.)[4][16]
| H | He | ||||||||||||||||||
| Li | Be | B | C | N | O | F | Ne | ||||||||||||
| Na | Mg | Al | Si | P | S | Cl | Ar | ||||||||||||
| K | Ca | Sc | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | Zn | Ga | Ge | As | Se | Br | Kr | ||
| Rb | Sr | Y | Zr | Nb | Mo | Tc | Ru | Rh | Pd | Ag | Cd | In | Sn | Sb | Te | I | Xe | ||
| Cs | Ba | La | Ce–Lu | Hf | Ta | W | Re | Os | Ir | Pt | Au | Hg | Tl | Pb | Bi | Po | At | Rn | |
| Fr | Ra | Ac | Th–Lr | Rf | Db | Sg | Bh | Hs | Mt | Ds | Rg | Cn | Nh | Fl | Mc | Lv | Ts | Og | |
| 119 | 120 | 121 | 122–141 | 142–155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | ||||||
| 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 |
Fricke et al.'s format is more focused on formal electron configurations than likely chemical behaviour. They place elements 156–164 in groups 4–12 because formally their configurations should be 7d2 through 7d10. However, they differ from the previous d-elements in that the 8s shell is not available for chemical bonding: instead, the 9s shell is. Thus element 164 with 7d109s0 is noted by Fricke et al. to be analogous to palladium with 4d105s0, and they consider elements 157–172 to have chemical analogies to groups 3–18 (though they are ambivalent on whether elements 165 and 166 are more like group 1 and 2 elements or more like group 11 and 12 elements, respectively). Thus, elements 157–164 are placed in their table in a group that the authors do not think is chemically most analogous.[17]
Nefedov
Vadim Nefedov (ru), Malvina Trzhaskovskaya, and Victor Yarzhemskii carried out calculations up to 164 (results published in 2006). They considered elements 158 through 164 to be homologues of groups 4 through 10, and not 6 through 12, noting similarities of electron configurations to the period 5 transition metals (e.g. element 159 7d49s1 vs Nb 4d45s1, element 160 7d59s1 vs Mo 4d55s1, element 162 7d79s1 vs Ru 4d75s1, element 163 7d89s1 vs Rh 4d85s1, element 164 7d109s0 vs Pd 4d105s0). They thus agree with Fricke et al. on the chemically most analogous groups, but differ from them in that Nefedov et al. actually place elements in the chemically most analogous groups. Rg and Cn are given an asterisk to reflect differing configurations from Au and Hg (in the original publication they are drawn as being displaced in the third dimension). In fact Cn probably has an analogous configuration to Hg, and the difference in configuration between Pt and Ds is not marked.[18]
| Cs | Ba | La–Lu | Hf | Ta | W | Re | Os | Ir | Pt | Au | Hg | Tl | Pb | Bi | Po | At | Rn |
| Fr | Ra | Ac–Lr | Rf | Db | Sg | Bh | Hs | Mt | Ds | Rg* | Cn* | Nh | Fl | Mc | Lv | Ts | Og |
| 119 | 120 | 121–157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 |
Pyykkö
Pekka Pyykkö used computer modeling to calculate the positions of elements up to Z = 172 and their possible chemical properties in an article published in 2011. He reproduced the orbital order of Fricke et al., and proposed a refinement of their table by formally assigning slots to elements 121–164 based on ionic configurations.[13]

In order to bookkeep the electrons, Pyykkö places some elements out of order: thus 139 and 140 are placed in groups 13 and 14 to reflect that the 8p1/2 shell needs to fill, and he distinguishes separate , 8p1/2, and 6f series.[13] Fricke et al. and Nefedov et al. do not attempt to break up these series.[17][18]
Kulsha
Computational chemist Andrey Kulsha has suggested two forms of the extended periodic table up to 172 that build on and refine Nefedov et al.'s versions up to 164 with reference to Pyykkö's calculations.[19] Based on their likely chemical properties, elements 157–172 are placed by both forms as eighth-period congeners of yttrium through xenon in the fifth period;[19] this extends Nefedov et al.'s placement of 157–164 under yttrium through palladium,[18] and agrees with the chemical analogies given by Fricke et al.[17]
Kulsha suggested two ways to deal with elements 121–156, that lack precise analogues among earlier elements. In his first form (2011, after Pyykkö's paper was published),[19] elements 121–138 and 139–156 are placed as two separate rows (together called "ultransition elements"), related by the addition of a 5g18 subshell into the core, as according to Pyykkö's calculations of oxidation states,[13] they should, respectively, mimic lanthanides and actinides.[19][20] In his second suggestion (2016), elements 121–142 form a g-block (as they have 5g activity), while elements 143–156 form an f-block placed under actinium through nobelium.[21]


Thus, period 8 emerges with 54 elements, and the next noble element after 118 is 172.[22]
Smits et al.
In 2023, Smits, Düllmann, Indelicato, Nazarewicz, and Schwerdtfeger made another attempt to place elements from 119 to 170 in the periodic table based on their electron configurations. The configurations of a few elements (121–124 and 168) did not allow them to be placed unambiguously. Element 145 appears twice, some places have double occupancy, and others are empty.[23]
| Cs | Ba | La | Ce | Pr | Nd | Pm | Sm | Eu | Gd | Tb | Dy | Ho | Er | Tm | Yb | Lu | Hf | Ta | W | Re | Os | Ir | Pt | Au | Hg | Tl | Pb | Bi | Po | At | Rn | |||||||||||||||||||
| Fr | Ra | Ac | Th | Pa | U | Np | Pu | Am | Cm | Bk | Cf | Es | Fm | Md | No | Lr | Rf | Db | Sg | Bh | Hs | Mt | Ds | Rg | Cn | Nh | Fl | Mc | Lv | Ts | Og | |||||||||||||||||||
| 119 | 120 | 125 | 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133/134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142/143 | 144 | 145 | 145 | 146 | 147 | 148/149 | 150 | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158/159 | 160 | 161 | 162 | 163 | 164 | 167 | |||||||||||
| 165 | 166 | 169 | 170 |
Searches for undiscovered elements
Synthesis attempts
Attempts have been made to synthesise the period 8 elements up to unbiseptium, except unbitrium. All such attempts have been unsuccessful. An attempt to synthesise ununennium, the first period 8 element, is ongoing as of 2025[update].
Ununennium (E119)
The synthesis of element 119 (ununennium) was first attempted in 1985 by bombarding a target of einsteinium-254 with calcium-48 ions at the superHILAC accelerator at Berkeley, California:
- 25499Es + 4820Ca → 302119* → no atoms
No atoms were identified, leading to a limiting cross section of 300 nb.[24] Later calculations suggest that the cross section of the 3n reaction (which would result in 299119 and three neutrons as products) would actually be six hundred thousand times lower than this upper bound, at 0.5 pb.[25]
From April to September 2012, an attempt to synthesize the isotopes 295119 and 296119 was made by bombarding a target of berkelium-249 with titanium-50 at the GSI Helmholtz Centre for Heavy Ion Research in Darmstadt, Germany.[26][27] Based on the theoretically predicted cross section, it was expected that an ununennium atom would be synthesized within five months of the beginning of the experiment.[28] Moreover, as berkelium-249 decays to californium-249 (the next element) with a short half-life of 327 days, this allowed elements 119 and 120 to be searched for simultaneously.[29]
- 24997Bk + 5022Ti → 299119* → no atoms
The experiment was originally planned to continue to November 2012,[30] but was stopped early to make use of the 249Bk target to confirm the synthesis of tennessine (thus changing the projectiles to 48Ca).[31] This reaction of 249Bk + 50Ti was predicted to be the most favorable practical reaction for formation of element 119,[27] as it is rather asymmetrical,[28] though also somewhat cold.[31] (254Es + 48Ca would be superior, but preparing milligram quantities of 254Es for a target is difficult.)[28] Nevertheless, the necessary change from the "silver bullet" 48Ca to 50Ti divides the expected yield of element 119 by about twenty, as the yield is strongly dependent on the asymmetry of the fusion reaction.[28]
Due to the predicted short half-lives, the GSI team used new "fast" electronics capable of registering decay events within microseconds.[27] No atoms of element 119 were identified, implying a limiting cross section of 70 fb.[31] The predicted actual cross section is around 40 fb, which is at the limits of current technology.[28]
The team at RIKEN in Wakō, Japan began bombarding curium-248 targets with a vanadium-51 beam in January 2018[32] to search for element 119. Curium was chosen as a target, rather than heavier berkelium or californium, as these heavier targets are difficult to prepare.[33] The 248Cm targets were provided by Oak Ridge National Laboratory. RIKEN developed a high-intensity vanadium beam.[34] The experiment began at a cyclotron while RIKEN upgraded its linear accelerators; the upgrade was completed in 2020.[35] Bombardment may be continued with both machines until the first event is observed; the experiment is currently running intermittently for at least 100 days a year.[36][33] The RIKEN team's efforts are being financed by the Emperor of Japan.[37] The team at the JINR plans to attempt synthesis of element 119 in the future, probably via the 243Am + 54Cr reaction, but a precise timeframe has not been publicly released.[38][39]
Unbinilium (E120)
Following their success in obtaining oganesson by the reaction between 249Cf and 48Ca in 2006, the team at the Joint Institute for Nuclear Research (JINR) in Dubna started similar experiments in March–April 2007, in hope of creating element 120 (unbinilium) from nuclei of 58Fe and 244Pu.[40][41] Isotopes of unbinilium are predicted to have alpha decay half-lives of the order of microseconds.[42][43] Initial analysis revealed that no atoms of element 120 were produced, providing a limit of 400 fb for the cross section at the energy studied.[44]
- 24494Pu + 5826Fe → 302120* → no atoms
The Russian team planned to upgrade their facilities before attempting the reaction again.[44]
In April 2007, the team at the GSI Helmholtz Centre for Heavy Ion Research in Darmstadt, Germany, attempted to create element 120 using uranium-238 and nickel-64:[45]
- 23892U + 6428Ni → 302120* → no atoms
No atoms were detected, providing a limit of 1.6 pb for the cross section at the energy provided. The GSI repeated the experiment with higher sensitivity in three separate runs in April–May 2007, January–March 2008, and September–October 2008, all with negative results, reaching a cross section limit of 90 fb.[45]
In June–July 2010, and again in 2011, after upgrading their equipment to allow the use of more radioactive targets, scientists at the GSI attempted the more asymmetrical fusion reaction:[46]
- 24896Cm + 5424Cr → 302120 → no atoms
It was expected that the change in reaction would quintuple the probability of synthesizing element 120,[47] as the yield of such reactions is strongly dependent on their asymmetry.[28] Three correlated signals were observed that matched the predicted alpha decay energies of 299120 and its daughter 295Og, as well as the experimentally known decay energy of its granddaughter 291Lv. However, the lifetimes of these possible decays were much longer than expected, and the results could not be confirmed.[48][49][46]
In August–October 2011, a different team at the GSI using the TASCA facility tried a new, even more asymmetrical reaction:[50][31]
- 24998Cf + 5022Ti → 299120* → no atoms
This was also tried unsuccessfully the next year during the aforementioned attempt to make element 119 in the 249Bk+50Ti reaction, as 249Bk decays to 249Cf. Because of its asymmetry,[51] the reaction between 249Cf and 50Ti was predicted to be the most favorable practical reaction for synthesizing unbinilium, although it is also somewhat cold. No unbinilium atoms were identified, implying a limiting cross-section of 200 fb.[31] Jens Volker Kratz predicted the actual maximum cross-section for producing element 120 by any of these reactions to be around 0.1 fb;[52] in comparison, the world record for the smallest cross section of a successful reaction was 30 fb for the reaction 209Bi(70Zn,n)278Nh,[28] and Kratz predicted a maximum cross-section of 20 fb for producing the neighbouring element 119.[52] If these predictions are accurate, then synthesizing element 119 would be at the limits of current technology, and synthesizing element 120 would require new methods.[52]
In May 2021, the JINR announced plans to investigate the 249Cf+50Ti reaction in their new facility. However, the 249Cf target would have had to be made by the Oak Ridge National Laboratory in the United States,[53] and after the Russian invasion of Ukraine began in February 2022, collaboration between the JINR and other institutes completely ceased due to sanctions.[54] Consequently, the JINR now plans to try the 248Cm+54Cr reaction instead. A preparatory experiment for the use of 54Cr projectiles was conducted in late 2023, successfully synthesising 288Lv in the 238U+54Cr reaction,[55] and the hope is for experiments to synthesise element 120 to begin by 2025.[56]
Starting from 2022,[34] plans have also been made to use 88-inch cyclotron in the Lawrence Berkeley National Laboratory (LBNL) in Berkeley, California, United States to attempt to make new elements using 50Ti projectiles.[57][58] First, the 244Pu+50Ti reaction was tested, successfully creating two atoms of 290Lv in 2024. Since this was successful, an attempt to make element 120 in the 249Cf+50Ti reaction is planned to begin in 2025.[59][60][61] The Lawrence Livermore National Laboratory (LLNL), which previously collaborated with the JINR, will collaborate with the LBNL on this project.[62]
Unbiunium (E121)
The synthesis of element 121 (unbiunium) was first attempted in 1977 by bombarding a target of uranium-238 with copper-65 ions at the Gesellschaft für Schwerionenforschung in Darmstadt, Germany:
- 23892U + 6529Cu → 303121* → no atoms
No atoms were identified.[11]
Unbibium (E122)
The first attempts to synthesize element 122 (unbibium) were performed in 1972 by Flerov et al. at the Joint Institute for Nuclear Research (JINR), using the heavy-ion induced hot fusion reactions:[10]
- 23892U + 66,6830Zn → 304, 306122* → no atoms
These experiments were motivated by early predictions on the existence of an island of stability at N = 184 and Z > 120. No atoms were detected and a yield limit of 5 nb (5,000 pb) was measured. Current results (see flerovium) have shown that the sensitivity of these experiments were too low by at least 3 orders of magnitude.[12]
In 2000, the Gesellschaft für Schwerionenforschung (GSI) Helmholtz Center for Heavy Ion Research performed a very similar experiment with much higher sensitivity:[10]
- 23892U + 7030Zn → 308122* → no atoms
These results indicate that the synthesis of such heavier elements remains a significant challenge and further improvements of beam intensity and experimental efficiency is required. The sensitivity should be increased to 1 fb in the future for better quality results.
Another unsuccessful attempt to synthesize element 122 was carried out in 1978 at the GSI Helmholtz Center, where a natural erbium target was bombarded with xenon-136 ions:[10]
- nat68Er + 13654Xe → 298, 300, 302, 303, 304, 306122* → no atoms
In particular, the reaction between 170Er and 136Xe was expected to yield alpha-emitters with half-lives of microseconds that would decay down to isotopes of flerovium with half-lives perhaps increasing up to several hours, as flerovium is predicted to lie near the center of the island of stability. After twelve hours of irradiation, nothing was found in this reaction. Following a similar unsuccessful attempt to synthesize element 121 from 238U and 65Cu, it was concluded that half-lives of superheavy nuclei must be less than one microsecond or the cross sections are very small.[63] More recent research into synthesis of superheavy elements suggests that both conclusions are true.[28][64] The two attempts in the 1970s to synthesize element 122 were both propelled by the research investigating whether superheavy elements could potentially be naturally occurring.[10]
Several experiments studying the fission characteristics of various superheavy compound nuclei such as 306122* were performed between 2000 and 2004 at the Flerov Laboratory of Nuclear Reactions. Two nuclear reactions were used, namely 248Cm + 58Fe and 242Pu + 64Ni.[10] The results reveal how superheavy nuclei fission predominantly by expelling closed shell nuclei such as 132Sn (Z = 50, N = 82). It was also found that the yield for the fusion-fission pathway was similar between 48Ca and 58Fe projectiles, suggesting a possible future use of 58Fe projectiles in superheavy element formation.[65]
Unbiquadium (E124)
Scientists at GANIL (Grand Accélérateur National d'Ions Lourds) attempted to measure the direct and delayed fission of compound nuclei of elements with Z = 114, 120, and 124 in order to probe shell effects in this region and to pinpoint the next spherical proton shell. This is because having complete nuclear shells (or, equivalently, having a magic number of protons or neutrons) would confer more stability on the nuclei of such superheavy elements, thus moving closer to the island of stability. In 2006, with full results published in 2008, the team provided results from a reaction involving the bombardment of a natural germanium target with uranium ions:
- 23892U + nat32Ge → 308, 310, 311, 312, 314124* → fission
The team reported that they had been able to identify compound nuclei fissioning with half-lives > 10−18 s. This result suggests a strong stabilizing effect at Z = 124 and points to the next proton shell at Z > 120, not at Z = 114 as previously thought. A compound nucleus is a loose combination of nucleons that have not arranged themselves into nuclear shells yet. It has no internal structure and is held together only by the collision forces between the target and projectile nuclei. It is estimated that it requires around 10−14 s for the nucleons to arrange themselves into nuclear shells, at which point the compound nucleus becomes a nuclide, and this number is used by IUPAC as the minimum half-life a claimed isotope must have to potentially be recognised as being discovered. Thus, the GANIL experiments do not count as a discovery of element 124.[10]
The fission of the compound nucleus 312124 was also studied in 2006 at the tandem ALPI heavy-ion accelerator at the Laboratori Nazionali di Legnaro (Legnaro National Laboratories) in Italy:[66]
- 23290Th + 8034Se → 312124* → fission
Similarly to previous experiments conducted at the JINR (Joint Institute for Nuclear Research), fission fragments clustered around doubly magic nuclei such as 132Sn (Z = 50, N = 82), revealing a tendency for superheavy nuclei to expel such doubly magic nuclei in fission.[65] The average number of neutrons per fission from the 312124 compound nucleus (relative to lighter systems) was also found to increase, confirming that the trend of heavier nuclei emitting more neutrons during fission continues into the superheavy mass region.[66]
Unbipentium (E125)
The first and only attempt to synthesize element 125 (unbipentium) was conducted in Dubna in 1970–1971 using zinc ions and an americium-243 target:[12]
- 24395Am + 66, 6830Zn → 309, 311125* → no atoms
No atoms were detected, and a cross section limit of 5 nb was determined. This experiment was motivated by the possibility of greater stability for nuclei around Z ~ 126 and N ~ 184,[12] though more recent research suggests the island of stability may instead lie at a lower atomic number (such as copernicium, Z = 112), and the synthesis of heavier elements such as element 125 will require more sensitive experiments.[28]
Unbihexium (E126)
The first and only attempt to synthesize element 126 (unbihexium), which was unsuccessful, was performed in 1971 at CERN (European Organization for Nuclear Research) by René Bimbot and John M. Alexander using the hot fusion reaction:[10]
- 23290Th + 8436Kr → 316126* → no atoms
High-energy (13–15 MeV) alpha particles were observed and taken as possible evidence for the synthesis of element 126. Subsequent unsuccessful experiments with higher sensitivity suggest that the 10 mb sensitivity of this experiment was too low; hence, the formation of element 126 nuclei in this reaction is highly unlikely.[8]
Unbiseptium (E127)
The first and only attempt to synthesize element 127 (unbiseptium), which was unsuccessful, was performed in 1978 at the UNILAC accelerator at the GSI Helmholtz Center, where a natural tantalum target was bombarded with xenon-136 ions:[10]
- nat73Ta + 13654Xe → 316, 317127* → no atoms
Searches in nature
A study in 1976 by a group of American researchers from several universities proposed that primordial superheavy elements, mainly livermorium, elements 124, 126, and 127, could be a cause of unexplained radiation damage (particularly radiohalos) in minerals.[8] This prompted many researchers to search for them in nature from 1976 to 1983. A group led by Tom Cahill, a professor at the University of California at Davis, claimed in 1976 that they had detected alpha particles and X-rays with the right energies to cause the damage observed, supporting the presence of these elements. In particular, the presence of long-lived (on the order of 109 years) nuclei of elements 124 and 126, along with their decay products, at an abundance of 10−11 relative to their possible congeners uranium and plutonium, was conjectured.[67] Others claimed that none had been detected, and questioned the proposed characteristics of primordial superheavy nuclei.[8] In particular, they cited that any such superheavy nuclei must have a closed neutron shell at N = 184 or N = 228, and this necessary condition for enhanced stability only exists in neutron deficient isotopes of livermorium or neutron rich isotopes of the other elements that would not be beta-stable[8] unlike most naturally occurring isotopes.[68] This activity was also proposed to be caused by nuclear transmutations in natural cerium, raising further ambiguity upon this claimed observation of superheavy elements.[8]
On April 24, 2008, a group led by Amnon Marinov at the Hebrew University of Jerusalem claimed to have found single atoms of 292122 in naturally occurring thorium deposits at an abundance of between 10−11 and 10−12 relative to thorium.[69] The claim of Marinov et al. was criticized by a part of the scientific community. Marinov claimed that he had submitted the article to the journals Nature and Nature Physics but both turned it down without sending it for peer review.[70] The 292122 atoms were claimed to be superdeformed or hyperdeformed isomers, with a half-life of at least 100 million years.[10]
A criticism of the technique, previously used in purportedly identifying lighter thorium isotopes by mass spectrometry,[71] was published in Physical Review C in 2008.[72] A rebuttal by the Marinov group was published in Physical Review C after the published comment.[73]
A repeat of the thorium experiment using the superior method of Accelerator Mass Spectrometry (AMS) failed to confirm the results, despite a 100-fold better sensitivity.[74] This result throws considerable doubt on the results of the Marinov collaboration with regard to their claims of long-lived isotopes of thorium,[71] roentgenium[75] and element 122.[69] It is still possible that traces of unbibium might only exist in some thorium samples, although this is unlikely.[10]
The possible extent of primordial superheavy elements on Earth today is uncertain. Even if they are confirmed to have caused the radiation damage long ago, they might now have decayed to mere traces, or even be completely gone.[76] It is also uncertain if such superheavy nuclei may be produced naturally at all, as spontaneous fission is expected to terminate the r-process responsible for heavy element formation between mass number 270 and 290, well before elements beyond 120 may be formed.[77]
A recent hypothesis tries to explain the spectrum of Przybylski's Star by naturally occurring flerovium and element 120.[78][79][80]
Predicted properties of eighth-period elements
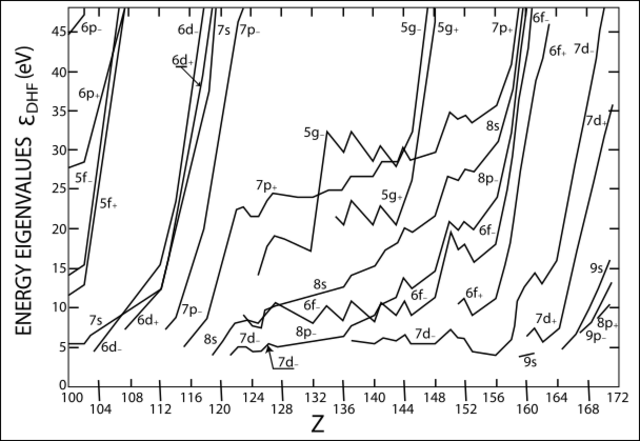
Element 118, oganesson, is the heaviest element that has been synthesized. The next two elements, elements 119 and 120, should form an 8s series and be an alkali and alkaline earth metal, respectively. Beyond element 120, the superactinide series is expected to begin, when the 8s electrons and the filling of the 8p1/2, 7d3/2, 6f, and 5g subshells determine the chemistry of these elements. Complete and accurate CCSD calculations are not available for elements beyond 122 because of the extreme complexity of the situation: the 5g, 6f, and 7d orbitals should have about the same energy level, and in the region of element 160, the 9s, 8p3/2, and 9p1/2 orbitals should also be about equal in energy. This will cause the electron shells to mix so that the block concept no longer applies very well, and will also result in novel chemical properties that will make positioning some of these elements in a periodic table very difficult.[15]
Chemical and physical properties
Elements 119 and 120
Some predicted properties of elements 119 and 120[4][15] Property 119 120 Standard atomic weight [322] [325] Group 1 2 Valence electron configuration 8s1 8s2 Stable oxidation states 1, 3 2, 4 First ionization energy 463.1 kJ/mol 563.3 kJ/mol Metallic radius 260 pm 200 pm Density 3 g/cm3 7 g/cm3 Melting point 0–30 °C (32–86 °F) 680 °C (1,300 °F) Boiling point 630 °C (1,200 °F) 1,700 °C (3,100 °F)
The first two elements of period 8 will be ununennium and unbinilium, elements 119 and 120. Their electron configurations should have the 8s orbital being filled. This orbital is relativistically stabilized and contracted; thus, elements 119 and 120 should be more like rubidium and strontium than their immediate neighbours above, francium and radium. Another effect of the relativistic contraction of the 8s orbital is that the atomic radii of these two elements should be about the same as those of francium and radium. They should behave like normal alkali and alkaline earth metals (albeit less reactive than their immediate vertical neighbours), normally forming +1 and +2 oxidation states, respectively, but the relativistic destabilization of the 7p3/2 subshell and the relatively low ionization energies of the 7p3/2 electrons should make higher oxidation states like +3 and +4 (respectively) possible as well.[4][15]
Superactinides
The superactinides may range from elements 121 through 157, which can be classified as the 5g and 6f elements of the eighth period, together with the first 7d element.[18] In the superactinide series, the 7d3/2, 8p1/2, 6f5/2 and 5g7/2 shells should all fill simultaneously.[16] This creates very complicated situations, so much so that complete and accurate CCSD calculations have been done only for elements 121 and 122.[15] The first superactinide, unbiunium or eka-actinium (element 121), should be similar to lanthanum and actinium:[81] its main oxidation state should be +3, although the closeness of the valence subshells' energy levels may permit higher oxidation states, just as in elements 119 and 120.[15] Relativistic stabilization of the 8p subshell should result in a ground-state 8s28p1 valence electron configuration for element 121, in contrast to the ds2 configurations of lanthanum and actinium;[15] nevertheless, this anomalous configuration does not appear to affect its calculated chemistry, which remains similar to that of actinium.[82] Its first ionization energy is predicted to be 429.4 kJ/mol, which would be lower than those of all known elements except for the alkali metals potassium, rubidium, caesium, and francium: this value is even lower than that of the period 8 alkali metal ununennium (463.1 kJ/mol). Similarly, the next superactinide, unbibium or eka-thorium (element 122), may be similar to cerium and thorium, with a main oxidation state of +4, but would have a ground-state 7d18s28p1 or 8s28p2 valence electron configuration,[83] unlike thorium's 6d27s2 configuration. Hence, its first ionization energy would be smaller than thorium's (Th: 6.3 eV; element 122: 5.6 eV) because of the greater ease of ionizing unbibium's 8p1/2 electron than thorium's 6d electron.[15] The collapse of the 5g orbital itself is delayed until around element 125 (unbipentium or eka-neptunium); the electron configurations of the 119-electron isoelectronic series are expected to be [Og]8s1 for elements 119 through 122, [Og]6f1 for elements 123 and 124, and [Og]5g1 for element 125 onwards.[84]
In the first few superactinides, the binding energies of the added electrons are predicted to be small enough that they can lose all their valence electrons; for example, unbihexium (element 126) could easily form a +8 oxidation state, and even higher oxidation states for the next few elements may be possible. Element 126 is also predicted to display a variety of other oxidation states: recent calculations have suggested a stable monofluoride 126F may be possible, resulting from a bonding interaction between the 5g orbital on element 126 and the 2p orbital on fluorine.[85] Other predicted oxidation states include +2, +4, and +6; +4 is expected to be the most usual oxidation state of unbihexium.[16] The superactinides from unbipentium (element 125) to unbiennium (element 129) are predicted to exhibit a +6 oxidation state and form hexafluorides, though 125F6 and 126F6 are predicted to be relatively weakly bound.[84] The bond dissociation energies are expected to greatly increase at element 127 and even more so at element 129. This suggests a shift from strong ionic character in fluorides of element 125 to more covalent character, involving the 8p orbital, in fluorides of element 129. The bonding in these superactinide hexafluorides is mostly between the highest 8p subshell of the superactinide and the 2p subshell of fluorine, unlike how uranium uses its 5f and 6d orbitals for bonding in uranium hexafluoride.[84]
Despite the ability of early superactinides to reach high oxidation states, it has been calculated that the 5g electrons will be most difficult to ionize; the 1256+ and 1267+ ions are expected to bear a 5g1 configuration, similar to the 5f1 configuration of the Np6+ ion.[13][84] Similar behavior is observed in the low chemical activity of the 4f electrons in lanthanides; this is a consequence of the 5g orbitals being small and deeply buried in the electron cloud.[13] The presence of electrons in g-orbitals, which do not exist in the ground state electron configuration of any currently known element, should allow presently unknown hybrid orbitals to form and influence the chemistry of the superactinides in new ways, although the absence of g electrons in known elements makes predicting superactinide chemistry more difficult.[4]
Some predicted compounds of the superactinides (X = a halogen)[13][84][86] 121 122 123 124 125 126 127 128 129 132 142 143 144 145 146 148 153 154 155 156 157 Compound 121X3 122X4 123X5 124X6 125F
125F6
125O2+2126F
126F6
126O4127F6 128F6 129F
129F6142X4
142X6143F6 144X6
144O2+2
144F8
144O4145F6 148O6 Analogs LaX3
AcX3CeX4
ThX4NpO2+2 ThF4 UF6
UO2+2
PuF8
PuO4UO6 Oxidation states 3 4 5 6 1, 6, 7 1, 2, 4, 6, 8 6 6 1, 6 6 4, 6 6, 8 3, 4, 5, 6, 8 6 8 12 3 0, 2 3, 5 2 3
In the later superactinides, the oxidation states should become lower. By element 132, the predominant most stable oxidation state will be only +6; this is further reduced to +3 and +4 by element 144, and at the end of the superactinide series it will be only +2 (and possibly even 0) because the 6f shell, which is being filled at that point, is deep inside the electron cloud and the 8s and 8p1/2 electrons are bound too strongly to be chemically active. The 5g shell should be filled at element 144 and the 6f shell at around element 154, and at this region of the superactinides the 8p1/2 electrons are bound so strongly that they are no longer active chemically, so that only a few electrons can participate in chemical reactions. Calculations by Fricke et al. predict that at element 154, the 6f shell is full and there are no d- or other electron wave functions outside the chemically inactive 8s and 8p1/2 shells. This may cause element 154 to be rather unreactive with noble gas-like properties.[4][15] Calculations by Pyykkö nonetheless expect that at element 155, the 6f shell is still chemically ionizable: 1553+ should have a full 6f shell, and the fourth ionization potential should be between those of terbium and dysprosium, both of which are known in the +4 state.[13]
Similarly to the lanthanide and actinide contractions, there should be a superactinide contraction in the superactinide series where the ionic radii of the superactinides are smaller than expected. In the lanthanides, the contraction is about 4.4 pm per element; in the actinides, it is about 3 pm per element. The contraction is larger in the lanthanides than in the actinides due to the greater localization of the 4f wave function as compared to the 5f wave function. Comparisons with the wave functions of the outer electrons of the lanthanides, actinides, and superactinides lead to a prediction of a contraction of about 2 pm per element in the superactinides; although this is smaller than the contractions in the lanthanides and actinides, its total effect is larger due to the fact that 32 electrons are filled in the deeply buried 5g and 6f shells, instead of just 14 electrons being filled in the 4f and 5f shells in the lanthanides and actinides, respectively.[4]
Pekka Pyykkö divides these superactinides into three series: a 5g series (elements 121 to 138), an 8p1/2 series (elements 139 to 140), and a 6f series (elements 141 to 155), also noting that there would be a great deal of overlapping between energy levels and that the 6f, 7d, or 8p1/2 orbitals could well also be occupied in the early superactinide atoms or ions. He also expects that they would behave more like "superlanthanides", in the sense that the 5g electrons would mostly be chemically inactive, similarly to how only one or two 4f electrons in each lanthanide are ever ionized in chemical compounds. He also predicted that the possible oxidation states of the superactinides might rise very high in the 6f series, to values such as +12 in element 148.[13]
Andrey Kulsha has called the elements 121 to 156 "ultransition" elements and has proposed to split them into two series of eighteen each, one from elements 121 to 138 and another from elements 139 to 156. The first would be analogous to the lanthanides, with oxidation states mainly ranging from +4 to +6, as the filling of the 5g shell dominates and neighbouring elements are very similar to each other, creating an analogy to uranium, neptunium, and plutonium. The second would be analogous to the actinides: at the beginning (around elements in the 140s) very high oxidation states would be expected as the 6f shell rises above the 7d one, but after that the typical oxidation states would lower and in elements in the 150s onwards the 8p1/2 electrons would stop being chemically active. Because the two rows are separated by the addition of a complete 5g18 subshell, they could be considered analogues of each other as well.[19][20]
As an example from the late superactinides, element 156 is expected to exhibit mainly the +2 oxidation state, on account of its electron configuration with easily removed 7d2 electrons over a stable [Og]5g186f148s28p21/2 core. It can thus be considered a heavier congener of nobelium, which likewise has a pair of easily removed 7s2 electrons over a stable [Rn]5f14 core, and is usually in the +2 state (strong oxidisers are required to obtain nobelium in the +3 state).[19] Its first ionization energy should be about 400 kJ/mol and its metallic radius approximately 170 picometers. With a relative atomic mass of around 445 Da,[4] it should be a very heavy metal with a density of around 26 g/cm3.
Elements 157 to 166
The 7d transition metals in period 8 are expected to be elements 157 to 166. Although the 8s and 8p1/2 electrons are bound so strongly in these elements that they should not be able to take part in any chemical reactions, the 9s and 9p1/2 levels are expected to be readily available for hybridization.[4][15] These 7d elements should be similar to the 4d elements yttrium through cadmium.[19] In particular, element 164 with a 7d109s0 electron configuration shows clear analogies with palladium with its 4d105s0 electron configuration.[16]
The noble metals of this series of transition metals are not expected to be as noble as their lighter homologues, due to the absence of an outer s shell for shielding and also because the 7d shell is strongly split into two subshells due to relativistic effects. This causes the first ionization energies of the 7d transition metals to be smaller than those of their lighter congeners.[4][15][16]
Theoretical interest in the chemistry of unhexquadium is largely motivated by theoretical predictions that it, especially the isotopes 472164 and 482164 (with 164 protons and 308 or 318 neutrons), would be at the center of a hypothetical second island of stability (the first being centered on copernicium, particularly the isotopes 291Cn, 293Cn, and 296Cn which are expected to have half-lives of centuries or millennia).[87][52][88][89]
Calculations predict that the 7d electrons of element 164 (unhexquadium) should participate very readily in chemical reactions, so that it should be able to show stable +6 and +4 oxidation states in addition to the normal +2 state in aqueous solutions with strong ligands. Element 164 should thus be able to form compounds like 164(CO)4, 164(PF3)4 (both tetrahedral like the corresponding palladium compounds), and 164(CN)2−2 (linear), which is very different behavior from that of lead, which element 164 would be a heavier homologue of if not for relativistic effects. Nevertheless, the divalent state would be the main one in aqueous solution (although the +4 and +6 states would be possible with stronger ligands), and unhexquadium(II) should behave more similarly to lead than unhexquadium(IV) and unhexquadium(VI).[15][16]
Element 164 is expected to be a soft Lewis acid and have Ahrlands softness parameter close to 4 eV. It should be at most moderately reactive, having a first ionization energy that should be around 685 kJ/mol, comparable to that of molybdenum.[4][16] Due to the lanthanide, actinide, and superactinide contractions, element 164 should have a metallic radius of only 158 pm, very close to that of the much lighter magnesium, despite its expected atomic weight of around 474 Da, which is about 19.5 times the atomic weight of magnesium.[4] This small radius and high weight cause it to be expected to have an extremely high density of around 46 g·cm−3, over twice that of osmium, currently the most dense element known, at 22.61 g·cm−3; element 164 should be the second most dense element in the first 172 elements in the periodic table, with only its neighbor unhextrium (element 163) being more dense (at 47 g·cm−3).[4] Metallic element 164 should have a very large cohesive energy (enthalpy of crystallization) due to its covalent bonds, most probably resulting in a high melting point. In the metallic state, element 164 should be quite noble and analogous to palladium and platinum. Fricke et al. suggested some formal similarities to oganesson, as both elements have closed-shell configurations and similar ionisation energies, although they note that while oganesson would be a very bad noble gas, element 164 would be a good noble metal.[16]
Elements 165 (unhexpentium) and 166 (unhexhexium), the last two 7d metals, should behave similarly to alkali and alkaline earth metals when in the +1 and +2 oxidation states, respectively. The 9s electrons should have ionization energies comparable to those of the 3s electrons of sodium and magnesium, due to relativistic effects causing the 9s electrons to be much more strongly bound than non-relativistic calculations would predict. Elements 165 and 166 should normally exhibit the +1 and +2 oxidation states, respectively, although the ionization energies of the 7d electrons are low enough to allow higher oxidation states like +3 for element 165. The oxidation state +4 for element 166 is less likely, creating a situation similar to the lighter elements in groups 11 and 12 (particularly gold and mercury).[4][15] As with mercury but not copernicium, ionization of element 166 to 1662+ is expected to result in a 7d10 configuration corresponding to the loss of the s-electrons but not the d-electrons, making it more analogous to the lighter "less relativistic" group 12 elements zinc, cadmium, and mercury.[13]
Some predicted properties of elements 156–166
The metallic radii and densities are first approximations.[4][13][15]
Most analogous group is given first, followed by other similar groups.[16]Property 156 157 158 159 160 161 162 163 164 165 166 Standard atomic weight [445] [448] [452] [456] [459] [463] [466] [470] [474] [477] [481] Group Yb group 3 4 5 6 7 8 9 10 11
(1)12
(2)Valence electron configuration 7d2 7d3 7d4 7d5 7d6 7d7 7d8 7d9 7d10 7d10 9s1 7d10 9s2 Stable oxidation states 2 3 4 1, 5 2, 6 3, 7 4, 8 5 0, 2, 4, 6 1, 3 2 First ionization energy 400 kJ/mol 450 kJ/mol 520 kJ/mol 340 kJ/mol 420 kJ/mol 470 kJ/mol 560 kJ/mol 620 kJ/mol 690 kJ/mol 520 kJ/mol 630 kJ/mol Metallic radius 170 pm 163 pm 157 pm 152 pm 148 pm 148 pm 149 pm 152 pm 158 pm 250 pm 200 pm Density 26 g/cm3 28 g/cm3 30 g/cm3 33 g/cm3 36 g/cm3 40 g/cm3 45 g/cm3 47 g/cm3 46 g/cm3 7 g/cm3 11 g/cm3
Elements 167 to 172
The next six elements on the periodic table are expected to be the last main-group elements in their period,[13] and are likely to be similar to the 5p elements indium through xenon.[19] In elements 167 to 172, the 9p1/2 and 8p3/2 shells will be filled. Their energy eigenvalues are so close together that they behave as one combined p-subshell, similar to the non-relativistic 2p and 3p subshells. Thus, the inert-pair effect does not occur and the most common oxidation states of elements 167 to 170 are expected to be +3, +4, +5, and +6, respectively. Element 171 (unseptunium) is expected to show some similarities to the halogens, showing various oxidation states ranging from −1 to +7, although its physical properties are expected to be closer to that of a metal. Its electron affinity is expected to be 3.0 eV, allowing it to form H171, analogous to a hydrogen halide. The 171− ion is expected to be a soft base, comparable to iodide (I−). Element 172 (unseptbium) is expected to be a noble gas with chemical behaviour similar to that of xenon, as their ionization energies should be very similar (Xe, 1170.4 kJ/mol; element 172, 1090 kJ/mol). The only main difference between them is that element 172, unlike xenon, is expected to be a liquid or a solid at standard temperature and pressure due to its much higher atomic weight.[4] Unseptbium is expected to be a strong Lewis acid, forming fluorides and oxides, similarly to its lighter congener xenon.[16]
Because of some analogy of elements 165–172 to periods 2 and 3, Fricke et al. considered them to form a ninth period of the periodic table, while the eighth period was taken by them to end at the noble metal element 164. This ninth period would be similar to the second and third period in having no transition metals.[16] That being said, the analogy is incomplete for elements 165 and 166; although they do start a new s-shell (9s), this is above a d-shell, making them chemically more similar to groups 11 and 12.[17]
Some predicted properties of elements 167–172
The metallic or covalent radii and densities are first approximations.[4][15][16]Property 167 168 169 170 171 172 Standard atomic weight [485] [489] [493] [496] [500] [504] Group 13 14 15 16 17 18 Valence electron configuration 9s2 9p1 9s2 9p2 9s2 9p2 8p1 9s2 9p2 8p2 9s2 9p2 8p3 9s2 9p2 8p4 Stable oxidation states 3 4 5 6 −1, 3, 7 0, 4, 6, 8 First ionization energy 620 kJ/mol 720 kJ/mol 800 kJ/mol 890 kJ/mol 984 kJ/mol 1090 kJ/mol Metallic or covalent radius 190 pm 180 pm 175 pm 170 pm 165 pm 220 pm Density 17 g/cm3 19 g/cm3 18 g/cm3 17 g/cm3 16 g/cm3 9 g/cm3
Beyond element 172
Beyond element 172, there is the potential to fill the 6g, 7f, 8d, 10s, 10p1/2, and perhaps 6h11/2 shells. These electrons would be very loosely bound, potentially rendering extremely high oxidation states reachable, though the electrons would become more tightly bound as the ionic charge rises. Thus, there will probably be another very long transition series, like the superactinides.[16]
In element 173 (unsepttrium), the outermost electron might enter the 6g7/2, 9p3/2, or 10s subshells. Because spin–orbit interactions would create a very large energy gap between these and the 8p3/2 subshell, this outermost electron is expected to be very loosely bound and very easily lost to form a 173+ cation. As a result, element 173 is expected to behave chemically like an alkali metal, and one that might be far more reactive than even caesium (francium and element 119 being less reactive than caesium due to relativistic effects):[90][19] the calculated ionisation energy for element 173 is 3.070 eV,[91] compared to the experimentally known 3.894 eV for caesium. Element 174 (unseptquadium) may add an 8d electron and form a closed-shell 1742+ cation; its calculated ionisation energy is 3.614 eV.[91]
Element 184 (unoctquadium) was significantly targeted in early predictions, as it was originally speculated that 184 would be a proton magic number: it is predicted to have an electron configuration of [172] 6g5 7f4 8d3, with at least the 7f and 8d electrons chemically active. Its chemical behaviour is expected to be similar to uranium and neptunium, as further ionisation past the +6 state (corresponding to removal of the 6g electrons) is likely to be unprofitable; the +4 state should be most common in aqueous solution, with +5 and +6 reachable in solid compounds.[4][16][92]
End of the periodic table
The number of physically possible elements is unknown. A low estimate is that the periodic table may end soon after the island of stability,[14] which is expected to center on Z = 126, as the extension of the periodic and nuclide tables is restricted by the proton and the neutron drip lines and stability toward alpha decay and spontaneous fission.[93] One calculation by Y. Gambhir et al., analyzing nuclear binding energy and stability in various decay channels, suggests a limit to the existence of bound nuclei at Z = 146.[94] Other predictions of an end to the periodic table include Z = 128 (John Emsley) and Z = 155 (Albert Khazan).[10]
Elements above the atomic number 137
It is a "folk legend" among physicists that Richard Feynman suggested that neutral atoms could not exist for atomic numbers greater than Z = 137, on the grounds that the relativistic Dirac equation predicts that the ground-state energy of the innermost electron in such an atom would be an imaginary number. Here, the number 137 arises as the inverse of the fine-structure constant. By this argument, neutral atoms cannot exist beyond atomic number 137, and therefore a periodic table of elements based on electron orbitals breaks down at this point. However, this argument presumes that the atomic nucleus is pointlike. A more accurate calculation must take into account the small, but nonzero, size of the nucleus, which is predicted to push the limit further to Z ≈ 173.[95]
Bohr model
The Bohr model exhibits difficulty for atoms with atomic number greater than 137, for the speed of an electron in a 1s electron orbital, v, is given by
where Z is the atomic number, and α is the fine-structure constant, a measure of the strength of electromagnetic interactions.[96] Under this approximation, any element with an atomic number of greater than 137 would require 1s electrons to be traveling faster than c, the speed of light. Hence, the non-relativistic Bohr model is inaccurate when applied to such an element.
Relativistic Dirac equation

The relativistic Dirac equation gives the ground state energy as
where m is the rest mass of the electron.[97] For Z > 137, the wave function of the Dirac ground state is oscillatory, rather than bound, and there is no gap between the positive and negative energy spectra, as in the Klein paradox.[98] More accurate calculations taking into account the effects of the finite size of the nucleus indicate that the binding energy first exceeds 2mc2 for Z > Zcr probably between 168 and 172.[99] For Z > Zcr, if the innermost orbital (1s) is not filled, the electric field of the nucleus will pull an electron out of the vacuum, resulting in the spontaneous emission of a positron.[100][101] This diving of the 1s subshell into the negative continuum has often been taken to constitute an "end" to the periodic table,[13][95][102] but in fact it does not impose such a limit, as such resonances can be interpreted as Gamow states. Nonetheless, the accurate description of such states in a multi-electron system, needed to extend calculations and the periodic table past Zcr ≈ 172, are still open problems.[99]
Atoms with atomic numbers above Zcr ≈ 172 have been termed supercritical atoms. Supercritical atoms cannot be totally ionised because their 1s subshell would be filled by spontaneous pair creation in which an electron-positron pair is created from the negative continuum, with the electron being bound and the positron escaping. However, the strong field around the atomic nucleus is restricted to a very small region of space, so that the Pauli exclusion principle forbids further spontaneous pair creation once the subshells that have dived into the negative continuum are filled. Elements 173–184 have been termed weakly supercritical atoms as for them only the 1s shell has dived into the negative continuum; the 2p1/2 shell is expected to join around element 185 and the 2s shell around element 245. Experiments have so far not succeeded in detecting spontaneous pair creation from assembling supercritical charges through the collision of heavy nuclei (e.g. colliding lead with uranium to momentarily give an effective Z of 174; uranium with uranium gives effective Z = 184 and uranium with californium gives effective Z = 190).[103]
Even though passing Zcr does not mean elements can no longer exist, the increasing concentration of the 1s density close to the nucleus would likely make these electrons more vulnerable to K electron capture as Zcr is approached. For such heavy elements, these 1s electrons would likely spend a significant fraction of time so close to the nucleus that they are actually inside it. This may pose another limit to the periodic table.[104]
Because of the factor of m, muonic atoms become supercritical at a much larger atomic number of around 2200, as muons are about 207 times as heavy as electrons.[99]
Quark matter
It has also been posited that in the region beyond A > 300, an entire "continent of stability" consisting of a hypothetical phase of stable quark matter, comprising freely flowing up and down quarks rather than quarks bound into protons and neutrons, may exist. Such a form of matter is theorized to be a ground state of baryonic matter with a greater binding energy per baryon than nuclear matter, favoring the decay of nuclear matter beyond this mass threshold into quark matter. If this state of matter exists, it could possibly be synthesized in the same fusion reactions leading to normal superheavy nuclei, and would be stabilized against fission as a consequence of its stronger binding that is enough to overcome Coulomb repulsion.[105]
Calculations published in 2020,[106] suggest stability of up-down quark matter (udQM) nuggets against conventional nuclei beyond A ~ 266, and also show that udQM nuggets become supercritical earlier (Zcr ~ 163, A ~ 609) than conventional nuclei (Zcr ~ 177, A ~ 480).
Nuclear properties
Magic numbers and the island of stability
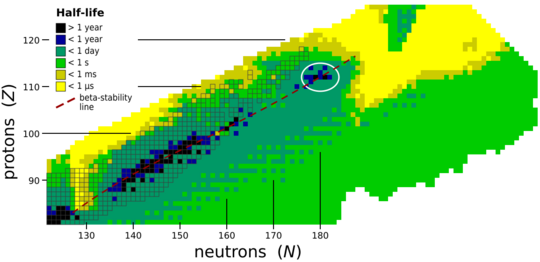
The stability of nuclei decreases greatly with the increase in atomic number after curium, element 96, so that all isotopes with an atomic number above 101 decay radioactively with a half-life under a day. No elements with atomic numbers above 82 (after lead) have stable isotopes.[107] Nevertheless, because of reasons not very well understood yet, there is a slight increased nuclear stability around atomic numbers 110–114, which leads to the appearance of what is known in nuclear physics as the "island of stability". This concept, proposed by University of California professor Glenn Seaborg, explains why superheavy elements last longer than predicted.[108]
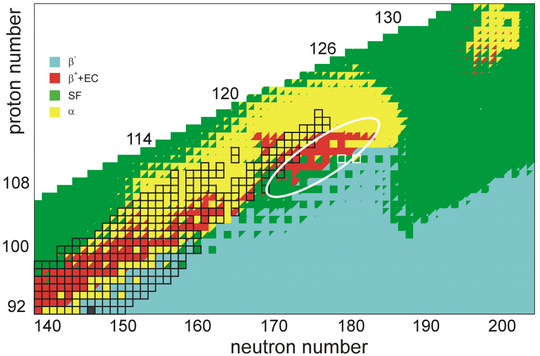
Calculations according to the Hartree–Fock–Bogoliubov method using the non-relativistic Skyrme interaction have proposed Z = 126 as a closed proton shell. In this region of the periodic table, N = 184, N = 196, and N = 228 have been suggested as closed neutron shells. Therefore, the isotopes of most interest are 310126, 322126, and 354126, for these might be considerably longer-lived than other isotopes. Element 126, having a magic number of protons, is predicted to be more stable than other elements in this region, and may have nuclear isomers with very long half-lives.[76] It is also possible that the island of stability is instead centered at 306122, which may be spherical and doubly magic.[52] Probably, the island of stability occurs around Z = 114–126 and N = 184, with lifetimes probably around hours to days. Beyond the shell closure at N = 184, spontaneous fission lifetimes should drastically drop below 10−15 seconds – too short for a nucleus to obtain an electron cloud and participate in any chemistry. That being said, such lifetimes are very model-dependent, and predictions range across many orders of magnitude.[99]
Taking nuclear deformation and relativistic effects into account, an analysis of single-particle levels predicts new magic numbers for superheavy nuclei at Z = 126, 138, 154, and 164 and N = 228, 308, and 318.[9][87] Therefore, in addition to the island of stability centered at 291Cn, 293Cn,[28] and 298Fl, further islands of stability may exist around the doubly magic 354126 as well as 472164 or 482164.[88][89] These nuclei are predicted to be beta-stable and decay by alpha emission or spontaneous fission with relatively long half-lives, and confer additional stability on neighboring N = 228 isotones and elements 152–168, respectively.[109] On the other hand, the same analysis suggests that proton shell closures may be relatively weak or even nonexistent in some cases such as 354126, meaning that such nuclei might not be doubly magic and stability will instead be primarily determined by strong neutron shell closures.[87] Additionally, due to the enormously greater forces of electromagnetic repulsion that must be overcome by the strong force at the second island (Z = 164),[110] it is possible that nuclei around this region only exist as resonances and cannot stay together for a meaningful amount of time. It is also possible that some of the superactinides between these series may not actually exist because they are too far from both islands,[110] in which case the periodic table might end around Z = 130.[16] The area of elements 121–156 where periodicity is in abeyance is quite similar to the gap between the two islands.[19]
Beyond element 164, the fissility line defining the limit of stability with respect to spontaneous fission may converge with the neutron drip line, posing a limit to the existence of heavier elements.[109] Nevertheless, further magic numbers have been predicted at Z = 210, 274, and 354 and N = 308, 406, 524, 644, and 772,[111] with two beta-stable doubly magic nuclei found at 616210 and 798274; the same calculation method reproduced the predictions for 298Fl and 472164. (The doubly magic nuclei predicted for Z = 354 are beta-unstable, with 998354 being neutron-deficient and 1126354 being neutron-rich.) Although additional stability toward alpha decay and fission are predicted for 616210 and 798274, with half-lives up to hundreds of microseconds for 616210,[111] there will not exist islands of stability as significant as those predicted at Z = 114 and 164. As the existence of superheavy elements is very strongly dependent on stabilizing effects from closed shells, nuclear instability and fission will likely determine the end of the periodic table beyond these islands of stability.[16][94][109]
The International Union of Pure and Applied Chemistry (IUPAC) defines an element to exist if its lifetime is longer than 10−14 seconds, which is the time it takes for the nucleus to form an electron cloud. However, a nuclide is generally considered to exist if its lifetime is longer than about 10−22 seconds, which is the time it takes for nuclear structure to form. Consequently, it is possible that some Z values can only be realised in nuclides and that the corresponding elements do not exist.[104]
It is also possible that no further islands actually exist beyond 126, as the nuclear shell structure gets smeared out (as the electron shell structure already is expected to be around oganesson) and low-energy decay modes become readily available.[112]
In some regions of the table of nuclides, there are expected to be additional regions of stability due to non-spherical nuclei that have different magic numbers than spherical nuclei do; the egg-shaped 270Hs (Z = 108, N = 162) is one such deformed doubly magic nucleus.[113] In the superheavy region, the strong Coulomb repulsion of protons may cause some nuclei, including isotopes of oganesson, to assume a bubble shape in the ground state with a reduced central density of protons, unlike the roughly uniform distribution inside most smaller nuclei.[114][115] Such a shape would have a very low fission barrier, however.[116] Even heavier nuclei in some regions, such as 342136 and 466156, may instead become toroidal or red blood cell-like in shape, with their own magic numbers and islands of stability, but they would also fragment easily.[117][118]
Predicted decay properties of undiscovered elements
As the main island of stability is thought to lie around 291Cn and 293Cn, undiscovered elements beyond oganesson may be very unstable and undergo alpha decay or spontaneous fission in microseconds or less. The exact region in which half-lives exceed one microsecond is unknown, though various models suggest that isotopes of elements heavier than unbinilium that may be produced in fusion reactions with available targets and projectiles will have half-lives under one microsecond and therefore may not be detected.[64] It is consistently predicted that there will exist regions of stability at N = 184 and N = 228, and possibly also at Z ~ 124 and N ~ 198. These nuclei may have half-lives of a few seconds and undergo predominantly alpha decay and spontaneous fission, though minor beta-plus decay (or electron capture) branches may also exist.[119] Outside these regions of enhanced stability, fission barriers are expected to drop significantly due to loss of stabilization effects, resulting in fission half-lives below 10−18 seconds, especially in even–even nuclei for which hindrance is even lower due to nucleon pairing.[109] In general, alpha decay half-lives are expected to increase with neutron number, from nanoseconds in the most neutron-deficient isotopes to seconds closer to the beta-stability line.[43] For nuclei with only a few neutrons more than a magic number, binding energy substantially drops, resulting in a break in the trend and shorter half-lives.[43] The most neutron deficient isotopes of these elements may also be unbound and undergo proton emission. Cluster decay (heavy particle emission) has also been proposed as an alternative decay mode for some isotopes,[120] posing yet another hurdle to identification of these elements.
Electron configurations
The following are expected electron configurations of elements 119–174 and 184. The symbol [Og] indicates the probable electron configuration of oganesson (Z = 118), which is currently the last known element. The configurations of the elements in this table are written starting with [Og] because oganesson is expected to be the last prior element with a closed-shell (inert gas) configuration, 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2 4f14 5d10 6p6 7s2 5f14 6d10 7p6. Similarly, the [172] in the configurations for elements 173, 174, and 184 denotes the likely closed-shell configuration of element 172.
Beyond element 123, no complete calculations are available and hence the data in this table must be taken as tentative.[16][90][121] In the case of element 123, and perhaps also heavier elements, several possible electron configurations are predicted to have very similar energy levels, such that it is very difficult to predict the ground state. All configurations that have been proposed (since it was understood that the Madelung rule probably stops working here) are included.[83][121][122]
The predicted block assignments up to 172 are Kulsha's,[21] following the expected available valence orbitals. There is, however, not a consensus in the literature as to how the blocks should work after element 138.
Chemical element Block Predicted electron configurations[15][16][18][90] 119 Uue Ununennium s-block [Og] 8s1 120 Ubn Unbinilium s-block [Og] 8s2 121 Ubu Unbiunium g-block [Og] 8s2 8p11/2[83] 122 Ubb Unbibium g-block [Og] 8s2 8p21/2[83]
[Og] 7d1 8s2 8p11/2123 Ubt Unbitrium g-block [Og] 6f1 8s2 8p21/2[123]
[Og] 6f1 7d1 8s2 8p11/2[83][121]
[Og] 6f2 8s2 8p11/2
[Og] 8s2 8p21/2 8p13/2[121]124 Ubq Unbiquadium g-block [Og] 6f2 8s2 8p21/2[83][123]
[Og] 6f3 8s2 8p11/2125 Ubp Unbipentium g-block [Og] 6f4 8s2 8p11/2[83]
[Og] 5g1 6f2 8s2 8p21/2[123]
[Og] 5g1 6f3 8s2 8p11/2
[Og] 8s2 0.81(5g1 6f2 8p21/2) + 0.17(5g1 6f1 7d2 8p11/2) + 0.02(6f3 7d1 8p11/2)126 Ubh Unbihexium g-block [Og] 5g1 6f4 8s2 8p11/2[83]
[Og] 5g2 6f2 8s2 8p21/2[123]
[Og] 5g2 6f3 8s2 8p11/2
[Og] 8s2 0.998(5g2 6f3 8p11/2) + 0.002(5g2 6f2 8p21/2)127 Ubs Unbiseptium g-block [Og] 5g2 6f3 8s2 8p21/2[83]
[Og] 5g3 6f2 8s2 8p21/2[123]
[Og] 8s2 0.88(5g3 6f2 8p21/2) + 0.12(5g3 6f1 7d2 8p11/2)128 Ubo Unbioctium g-block [Og] 5g3 6f3 8s2 8p21/2[83]
[Og] 5g4 6f2 8s2 8p21/2[123]
[Og] 8s2 0.88(5g4 6f2 8p21/2) + 0.12(5g4 6f1 7d2 8p11/2)129 Ube Unbiennium g-block [Og] 5g4 6f3 7d1 8s2 8p11/2
[Og] 5g4 6f3 8s2 8p21/2[83][123]
[Og] 5g5 6f2 8s2 8p21/2
[Og] 5g4 6f3 7d1 8s2 8p11/2130 Utn Untrinilium g-block [Og] 5g5 6f3 7d1 8s2 8p11/2
[Og] 5g5 6f3 8s2 8p21/2[83][123]
[Og] 5g6 6f2 8s2 8p21/2
[Og] 5g5 6f3 7d1 8s2 8p11/2131 Utu Untriunium g-block [Og] 5g6 6f3 8s2 8p21/2[83][123]
[Og] 5g7 6f2 8s2 8p21/2
[Og] 8s2 0.86(5g6 6f3 8p21/2) + 0.14(5g6 6f2 7d2 8p11/2)132 Utb Untribium g-block [Og] 5g7 6f3 8s2 8p21/2[123]
[Og] 5g8 6f2 8s2 8p21/2133 Utt Untritrium g-block [Og] 5g8 6f3 8s2 8p21/2[123] 134 Utq Untriquadium g-block [Og] 5g8 6f4 8s2 8p21/2[123] 135 Utp Untripentium g-block [Og] 5g9 6f4 8s2 8p21/2[123] 136 Uth Untrihexium g-block [Og] 5g10 6f4 8s2 8p21/2[123] 137 Uts Untriseptium g-block [Og] 5g11 6f4 8s2 8p21/2[123] 138 Uto Untrioctium g-block [Og] 5g12 6f4 8s2 8p21/2[123]
[Og] 5g12 6f3 7d1 8s2 8p21/2139 Ute Untriennium g-block [Og] 5g13 6f3 7d1 8s2 8p21/2[123]
[Og] 5g13 6f2 7d2 8s2 8p21/2140 Uqn Unquadnilium g-block [Og] 5g14 6f3 7d1 8s2 8p21/2[123]
[Og] 5g15 6f1 8s2 8p21/2 8p23/2141 Uqu Unquadunium g-block [Og] 5g15 6f2 7d2 8s2 8p21/2[123] 142 Uqb Unquadbium g-block [Og] 5g16 6f2 7d2 8s2 8p21/2[123] 143 Uqt Unquadtrium f-block [Og] 5g17 6f2 7d2 8s2 8p21/2[123] 144 Uqq Unquadquadium f-block [Og] 5g18 6f2 7d2 8s2 8p21/2[123]
[Og] 5g18 6f1 7d3 8s2 8p21/2
[Og] 5g17 6f2 7d3 8s2 8p21/2
[Og] 8s2 0.95(5g17 6f2 7d3 8p21/2) + 0.05(5g17 6f4 7d1 8p21/2)145 Uqp Unquadpentium f-block [Og] 5g18 6f3 7d2 8s2 8p21/2[123] 146 Uqh Unquadhexium f-block [Og] 5g18 6f4 7d2 8s2 8p21/2[123] 147 Uqs Unquadseptium f-block [Og] 5g18 6f5 7d2 8s2 8p21/2[123] 148 Uqo Unquadoctium f-block [Og] 5g18 6f6 7d2 8s2 8p21/2[123] 149 Uqe Unquadennium f-block [Og] 5g18 6f6 7d3 8s2 8p21/2[123] 150 Upn Unpentnilium f-block [Og] 5g18 6f6 7d4 8s2 8p21/2
[Og] 5g18 6f7 7d3 8s2 8p21/2[123]151 Upu Unpentunium f-block [Og] 5g18 6f8 7d3 8s2 8p21/2[123] 152 Upb Unpentbium f-block [Og] 5g18 6f9 7d3 8s2 8p21/2[123] 153 Upt Unpenttrium f-block [Og] 5g18 6f10 7d3 8s2 8p21/2
[Og] 5g18 6f11 7d2 8s2 8p21/2[123]154 Upq Unpentquadium f-block [Og] 5g18 6f11 7d3 8s2 8p21/2
[Og] 5g18 6f12 7d2 8s2 8p21/2[123]155 Upp Unpentpentium f-block [Og] 5g18 6f12 7d3 8s2 8p21/2
[Og] 5g18 6f13 7d2 8s2 8p21/2[123]156 Uph Unpenthexium f-block [Og] 5g18 6f13 7d3 8s2 8p21/2
[Og] 5g18 6f14 7d2 8s2 8p21/2[123]157 Ups Unpentseptium d-block [Og] 5g18 6f14 7d3 8s2 8p21/2[123] 158 Upo Unpentoctium d-block [Og] 5g18 6f14 7d4 8s2 8p21/2[123] 159 Upe Unpentennium d-block [Og] 5g18 6f14 7d5 8s2 8p21/2
[Og] 5g18 6f14 7d4 8s2 8p21/2 9s1[123]160 Uhn Unhexnilium d-block [Og] 5g18 6f14 7d6 8s2 8p21/2
[Og] 5g18 6f14 7d5 8s2 8p21/2 9s1[123]161 Uhu Unhexunium d-block [Og] 5g18 6f14 7d7 8s2 8p21/2
[Og] 5g18 6f14 7d6 8s2 8p21/2 9s1[123]162 Uhb Unhexbium d-block [Og] 5g18 6f14 7d8 8s2 8p21/2
[Og] 5g18 6f14 7d7 8s2 8p21/2 9s1[123]163 Uht Unhextrium d-block [Og] 5g18 6f14 7d9 8s2 8p21/2
[Og] 5g18 6f14 7d8 8s2 8p21/2 9s1[123]164 Uhq Unhexquadium d-block [Og] 5g18 6f14 7d10 8s2 8p21/2[123] 165 Uhp Unhexpentium d-block [Og] 5g18 6f14 7d10 8s2 8p21/2 9s1[123] 166 Uhh Unhexhexium d-block [Og] 5g18 6f14 7d10 8s2 8p21/2 9s2[123] 167 Uhs Unhexseptium p-block [Og] 5g18 6f14 7d10 8s2 8p21/2 9s2 9p11/2
[Og] 5g18 6f14 7d10 8s2 8p21/2 8p13/2 9s2[123]168 Uho Unhexoctium p-block [Og] 5g18 6f14 7d10 8s2 8p21/2 9s2 9p21/2
[Og] 5g18 6f14 7d10 8s2 8p21/2 8p23/2 9s2[123]169 Uhe Unhexennium p-block [Og] 5g18 6f14 7d10 8s2 8p21/2 8p13/2 9s2 9p21/2
[Og] 5g18 6f14 7d10 8s2 8p21/2 8p33/2 9s2[123]170 Usn Unseptnilium p-block [Og] 5g18 6f14 7d10 8s2 8p21/2 8p23/2 9s2 9p21/2
[Og] 5g18 6f14 7d10 8s2 8p21/2 8p43/2 9s2[123]171 Usu Unseptunium p-block [Og] 5g18 6f14 7d10 8s2 8p21/2 8p33/2 9s2 9p21/2
[Og] 5g18 6f14 7d10 8s2 8p21/2 8p43/2 9s2 9p11/2[123]172 Unseptbium p-block [Og] 5g18 6f14 7d10 8s2 8p21/2 8p43/2 9s2 9p21/2[123] 173 Ust Unsepttrium ? [172] 6g1
[172] 9p13/2
[172] 10s1[91]174 Usq Unseptquadium ? [172] 8d1 10s1[91] ... ... ... ... ... 184 Uoq Unoctquadium ? [172] 6g5 7f4 8d3
See also
References
- ↑ 1.0 1.1 Seaborg, Glenn T. (August 26, 1996). "An Early History of LBNL". http://www.lbl.gov/LBL-PID/Nobelists/Seaborg/65th-anniv/29.html.
- ↑ 2.0 2.1 Frazier, K. (1978). "Superheavy Elements". Science News 113 (15): 236–238. doi:10.2307/3963006.
- ↑ Element 122 was claimed to exist naturally in April 2008, but this claim was widely believed to be erroneous. "Heaviest element claim criticised". Rsc.org. 2008-05-02. http://www.rsc.org/chemistryworld/News/2008/May/02050802.asp.
- ↑ 4.00 4.01 4.02 4.03 4.04 4.05 4.06 4.07 4.08 4.09 4.10 4.11 4.12 4.13 4.14 4.15 4.16 4.17 4.18 4.19 Fricke, B.; Greiner, W.; Waber, J. T. (1971). "The continuation of the periodic table up to Z = 172. The chemistry of superheavy elements". Theoretica Chimica Acta 21 (3): 235–260. doi:10.1007/BF01172015.
- ↑ "Kernchemie". http://www.kernchemie.de/Transactinides/Transactinide-2/transactinide-2.html.
- ↑ Schiff, L. I.; Snyder, H.; Weinberg, J. (1940). "On the Existence of Stationary States of the Mesotron Field". Physical Review 57 (4): 315–318. doi:10.1103/PhysRev.57.315. Bibcode: 1940PhRv...57..315S.
- ↑ Kragh, Helge (2018). From Transuranic to Superheavy Elements: A Story of Dispute and Creation. Springer. pp. 6–10. ISBN 978-3-319-75813-8.
- ↑ 8.0 8.1 8.2 8.3 8.4 8.5 8.6 8.7 Hoffman, D.C; Ghiorso, A.; Seaborg, G.T. (2000). The Transuranium People: The Inside Story. Imperial College Press. ISBN 978-1-86094-087-3.
- ↑ 9.0 9.1 Maly, J.; Walz, D.R. (1980). "Search for superheavy elements among fossil fission tracks in zircon". http://www.slac.stanford.edu/pubs/slacpubs/2500/slac-pub-2554.pdf.
- ↑ 10.00 10.01 10.02 10.03 10.04 10.05 10.06 10.07 10.08 10.09 10.10 10.11 10.12 Emsley, John (2011). Nature's Building Blocks: An A-Z Guide to the Elements (New ed.). New York, NY: Oxford University Press. p. 588. ISBN 978-0-19-960563-7.
- ↑ 11.0 11.1 Hofmann, Sigurd (2002). On Beyond Uranium. Taylor & Francis. p. 105. ISBN 978-0-415-28496-7. https://archive.org/details/onbeyonduraniumj0000hofm/page/105.
- ↑ 12.0 12.1 12.2 12.3 Epherre, M.; Stephan, C. (1975). "Les éléments superlourds" (in fr). Le Journal de Physique Colloques 11 (36): C5–159–164. doi:10.1051/jphyscol:1975541. https://core.ac.uk/download/pdf/46775464.pdf.
- ↑ 13.00 13.01 13.02 13.03 13.04 13.05 13.06 13.07 13.08 13.09 13.10 13.11 13.12 Pyykkö, Pekka (2011). "A suggested periodic table up to Z≤ 172, based on Dirac–Fock calculations on atoms and ions". Physical Chemistry Chemical Physics 13 (1): 161–8. doi:10.1039/c0cp01575j. PMID 20967377. Bibcode: 2011PCCP...13..161P.
- ↑ 14.0 14.1 Seaborg, Glenn T. (c. 2006). "transuranium element (chemical element)". Encyclopædia Britannica. https://www.britannica.com/EBchecked/topic/603220/transuranium-element. Retrieved 2010-03-16.
- ↑ 15.00 15.01 15.02 15.03 15.04 15.05 15.06 15.07 15.08 15.09 15.10 15.11 15.12 15.13 15.14 15.15 Hoffman, Darleane C.; Lee, Diana M.; Pershina, Valeria (2006). "Transactinides and the future elements". in Morss; Edelstein, Norman M.; Fuger, Jean. The Chemistry of the Actinide and Transactinide Elements (3rd ed.). Dordrecht, The Netherlands: Springer Science+Business Media. ISBN 978-1-4020-3555-5.
- ↑ 16.00 16.01 16.02 16.03 16.04 16.05 16.06 16.07 16.08 16.09 16.10 16.11 16.12 16.13 16.14 16.15 16.16 16.17 16.18 Fricke, Burkhard (1975). "Superheavy elements: a prediction of their chemical and physical properties". Recent Impact of Physics on Inorganic Chemistry. Structure and Bonding 21: 89–144. doi:10.1007/BFb0116498. ISBN 978-3-540-07109-9. https://archive.org/details/recentimpactofph0000unse/page/89. Retrieved 4 October 2013.
- ↑ 17.0 17.1 17.2 17.3 Fricke, Burkhard; Waber, J. T. (1971). "Theoretical Predictions of the Chemistry of Superheavy Elements: Continuation of the Periodic Table up to Z=184". Actinides Reviews 1: 433–485. https://kobra.uni-kassel.de/bitstream/handle/123456789/2008100124269/Fricke_theoretical_1971.pdf. Retrieved 5 January 2024.
- ↑ 18.0 18.1 18.2 18.3 18.4 Nefedov, V.I.; Trzhaskovskaya, M.B.; Yarzhemskii, V.G. (2006). "Electronic Configurations and the Periodic Table for Superheavy Elements". Doklady Physical Chemistry 408 (2): 149–151. doi:10.1134/S0012501606060029. ISSN 0012-5016. http://www.primefan.ru/stuff/chem/nefedov.pdf.
- ↑ 19.00 19.01 19.02 19.03 19.04 19.05 19.06 19.07 19.08 19.09 Kulsha, Andrey (2011). "Есть ли граница у таблицы Менделеева?". in Kolevich, T. A. (in ru). Удивительный мир веществ и их превращений. Minsk: Национальный институт образования (National Institute of Education). pp. 5–19. ISBN 978-985-465-920-6. http://www.primefan.ru/stuff/chem/ptable/ptable.pdf. Retrieved 8 September 2018.
- ↑ 20.0 20.1 Sicius, Hermann (2021) (in de). Handbuch der chemischen Elemente. Springer. p. 1085. "Kulsha nennt die 36 Elemente zwischen 121 und 156 "Ultransition Elements" und schlägt vor, sie in zwei Serien aufzuteilen, in eine von 121 bis 138 und eine zweite von 139 bis 156. Die erste ähnelte eher den Lanthanoiden (Seltenerden), die zweite mehr den Actinoiden."
- ↑ 21.0 21.1 "Feasible electron configurations of dications up to Z = 172". http://www.primefan.ru/stuff/chem/ptable/dications.html.
- ↑ Wothers, Peter (2019). Antimony, Gold, and Jupiter's Wolf. Oxford University Press. p. vii. ISBN 978-0-19-965272-3. "It's possible that other elements might be synthesized—research is certainly ongoing—but it's unlikely that the table will ever appear as neat again, since to fill the next row, another fifty-four elements would need to be made."
- ↑ Smits, Odile R.; Düllmann, Christoph E.; Indelicato, Paul; Nazarewicz, Witold; Schwerdtfeger, Peter (2023). "The quest for superheavy elements and the limit of the periodic table". Nature Reviews Physics 6 (2): 86–98. doi:10.1038/s42254-023-00668-y.
- ↑ Lougheed, R. et al. (1985). "Search for superheavy elements using 48Ca + 254Esg reaction". Physical Review C 32 (5): 1760–1763. doi:10.1103/PhysRevC.32.1760. PMID 9953034. Bibcode: 1985PhRvC..32.1760L.
- ↑ Feng, Z; Jin, G.; Li, J.; Scheid, W. (2009). "Production of heavy and superheavy nuclei in massive fusion reactions". Nuclear Physics A 816 (1): 33. doi:10.1016/j.nuclphysa.2008.11.003. Bibcode: 2009NuPhA.816...33F.
- ↑ Modern alchemy: Turning a line, The Economist, May 12, 2012.
- ↑ 27.0 27.1 27.2 Superheavy Element Search Campaign at TASCA . J. Khuyagbaatar
- ↑ 28.00 28.01 28.02 28.03 28.04 28.05 28.06 28.07 28.08 28.09 Zagrebaev, Valeriy; Karpov, Alexander; Greiner, Walter (2013). "Future of superheavy element research: Which nuclei could be synthesized within the next few years?". Journal of Physics 420 (1). doi:10.1088/1742-6596/420/1/012001. Bibcode: 2013JPhCS.420a2001Z. http://nrv.jinr.ru/pdf_file/J_phys_2013.pdf. Retrieved 2017-04-05.
- ↑ Khuyagbaatar, J. et al. (2020). "Search for elements 119 and 120". Physical Review C 102 (6): 064602. doi:10.1103/PhysRevC.102.064602. Bibcode: 2020PhRvC.102f4602K. https://jyx.jyu.fi/bitstream/handle/123456789/73027/2/khuyagbaatarym0812.pdf. Retrieved 25 January 2021.
- ↑ "Search for element 119: Christoph E. Düllmann for the TASCA E119 collaboration". https://www-win.gsi.de/tasca12/program/contributions/TASCA12_Duellmann.pdf.
- ↑ 31.0 31.1 31.2 31.3 31.4 Yakushev, A. (2012). "Superheavy Element Research at TASCA". http://asrc.jaea.go.jp/soshiki/gr/chiba_gr/workshop3/%26Yakushev.pdf.
- ↑ Sakai, Hideyuki; Haba, Hiromitsu; Morimoto, Kouji; Sakamoto, Naruhiko (9 December 2022). "Facility upgrade for superheavy-element research at RIKEN". The European Physical Journal A 58 (238): 238. doi:10.1140/epja/s10050-022-00888-3. PMID 36533209. Bibcode: 2022EPJA...58..238S.
- ↑ 33.0 33.1 Sakai, Hideyuki (27 February 2019). "Search for a New Element at RIKEN Nishina Center". http://www0.mi.infn.it/~colo/slides_27_2_19/2019-2_Milano-WS_sakai.pdf.
- ↑ 34.0 34.1 Gates, J.; Pore, J.; Crawford, H.; Shaughnessy, D.; Stoyer, M. A. (25 October 2022). The Status and Ambitions of the US Heavy Element Program. doi:10.2172/1896856. https://www.osti.gov/servlets/purl/1896856. Retrieved 13 November 2022.
- ↑ Sakurai, Hiroyoshi (1 April 2020). "Greeting | RIKEN Nishina Center". https://www.nishina.riken.jp/about/greeting_e.html. "With the completion of the upgrade of the linear accelerator and BigRIPS at the beginning of 2020, the RNC aims to synthesize new elements from element 119 and beyond."
- ↑ Ball, P. (2019). "Extreme chemistry: experiments at the edge of the periodic table". Nature 565 (7741): 552–555. doi:10.1038/d41586-019-00285-9. ISSN 1476-4687. PMID 30700884. Bibcode: 2019Natur.565..552B. https://www.nature.com/magazine-assets/d41586-019-00285-9/d41586-019-00285-9.pdf. ""We started the search for element 119 last June," says RIKEN researcher Hideto En'yo. "It will certainly take a long time — years and years — so we will continue the same experiment intermittently for 100 or more days per year, until we or somebody else discovers it."".
- ↑ Chapman, Kit; Turner, Kristy (13 February 2018). "The hunt is on". Royal Society of Chemistry. https://eic.rsc.org/feature/the-hunt-is-on/3008580.article. "The hunt for element 113 was almost abandoned because of lack of resources, but this time Japan's emperor is bankrolling Riken's efforts to extend the periodic table to its eighth row."
- ↑ Joint Institute for Nuclear Research (24 July 2021). "JINR presented largest Periodic Table to Dubna". Joint Institute for Nuclear Research. http://www.jinr.ru/posts/jinr-presented-largest-periodic-table-to-dubna/.
- ↑ "Superheavy Element Factory: overview of obtained results". Joint Institute for Nuclear Research. 24 August 2023. http://www.jinr.ru/posts/superheavy-element-factory-overview-of-obtained-results/.
- ↑ "A New Block on the Periodic Table". Lawrence Livermore National Laboratory. April 2007. https://www.llnl.gov/str/April07/pdfs/04_07.4.pdf.
- ↑ Itkis, M. G.; Oganessian, Yu. Ts. (2007). "Synthesis of New Nuclei and Study of Nuclear Properties and Heavy-Ion Reaction Mechanisms". Joint Institute for Nuclear Research. http://wwwinfo.jinr.ru/plan/ptp-2007/e751004.htm.
- ↑ Chowdhury, P. Roy; Samanta, C.; Basu, D. N. (2008). "Search for long lived heaviest nuclei beyond the valley of stability". Physical Review C 77 (4). doi:10.1103/PhysRevC.77.044603. Bibcode: 2008PhRvC..77d4603C.
- ↑ 43.0 43.1 43.2 Chowdhury, R. P.; Samanta, C.; Basu, D.N. (2008). "Nuclear half-lives for α -radioactivity of elements with 100 ≤ Z ≤ 130". Atomic Data and Nuclear Data Tables 94 (6): 781–806. doi:10.1016/j.adt.2008.01.003. Bibcode: 2008ADNDT..94..781C.
- ↑ 44.0 44.1 Oganessian, Yu. Ts.; Utyonkov, V.; Lobanov, Yu.; Abdullin, F.; Polyakov, A.; Sagaidak, R.; Shirokovsky, I.; Tsyganov, Yu. et al. (2009). "Attempt to produce element 120 in the 244Pu+58Fe reaction". Phys. Rev. C 79 (2). doi:10.1103/PhysRevC.79.024603. Bibcode: 2009PhRvC..79b4603O.
- ↑ 45.0 45.1 Hoffman, S. (2008). Probing shell effects at Z=120 and N=184 (Report). GSI Scientific Report. p. 131.
- ↑ 46.0 46.1 Hofmann, S.; Heinz, S.; Mann, R.; Maurer, J.; Münzenberg, G.; Antalic, S.; Barth, W.; Burkhard, H. G. et al. (2016). "Review of even element super-heavy nuclei and search for element 120". The European Physical Journal A 2016 (52): 180. doi:10.1140/epja/i2016-16180-4. Bibcode: 2016EPJA...52..180H. https://zenodo.org/record/897926.
- ↑ GSI (2012-04-05). "Searching for the island of stability". GSI. https://www.gsi.de/de/work/forschung/nustarenna/nustarenna_divisions/she_physik/research/super_heavy_elements/future_projects.htm.
- ↑ Adcock, Colin (2 October 2015). "Weighty matters: Sigurd Hofmann on the heaviest of nuclei". https://jphysplus.iop.org/2015/10/02/weighty-matters-sigurd-hofmann-on-the-heaviest-of-nuclei/.
- ↑ Hofmann, S. (2015-05-12), "Search for isotopes of element 120 on the island of shn", Exotic Nuclei (WORLD SCIENTIFIC): pp. 213–224, doi:10.1142/9789814699464_0023, ISBN 978-981-4699-45-7, Bibcode: 2015exon.conf..213H, https://www.worldscientific.com/doi/abs/10.1142/9789814699464_0023, retrieved 2022-02-27
- ↑ Düllmann, C. E. (20 October 2011). "Superheavy Element Research: News from GSI and Mainz". http://www.yumpu.com/en/document/view/7293741/superheavy-element-research-superheavy-element-research.
- ↑ Siwek-Wilczyńska, K.; Cap, T.; Wilczyński, J. (April 2010). "How can one synthesize the element Z = 120?". International Journal of Modern Physics E 19 (4): 500. doi:10.1142/S021830131001490X. Bibcode: 2010IJMPE..19..500S.
- ↑ 52.0 52.1 52.2 52.3 52.4 Kratz, J. V. (5 September 2011). "The Impact of Superheavy Elements on the Chemical and Physical Sciences". 4th International Conference on the Chemistry and Physics of the Transactinide Elements. https://tan11.jinr.ru/pdf/06_Sep/S_1/02_Kratz.pdf. Retrieved 27 August 2013.
- ↑ Sokolova, Svetlana; Popeko, Andrei (24 May 2021). "How are new chemical elements born?". JINR. http://www.jinr.ru/posts/how-are-new-chemical-elements-born/. "Previously, we worked mainly with calcium. This is element 20 in the Periodic Table. It was used to bombard the target. And the heaviest element that can be used to make a target is californium, 98. Accordingly, 98 + 20 is 118. That is, to get element 120, we need to proceed to the next particle. This is most likely titanium: 22 + 98 = 120.
There is still much work to adjust the system. I don't want to get ahead of myself, but if we can successfully conduct all the model experiments, then the first experiments on the synthesis of element 120 will probably start this year." - ↑ Ahuja, Anjana (18 October 2023). "Even the periodic table must bow to the reality of war". Financial Times. https://www.ft.com/content/6b6b0afc-39b2-4955-af5a-d0ea6b4d8306.
- ↑ "В ЛЯР ОИЯИ впервые в мире синтезирован ливерморий-288" (in ru). Joint Institute for Nuclear Research. 23 October 2023. http://www.jinr.ru/posts/v-lyar-oiyai-vpervye-v-mire-sintezirovan-livermorij-288/.
- ↑ Mayer, Anastasiya (31 May 2023). ""Большинство наших партнеров гораздо мудрее политиков"" (in ru). Vedomosti. https://www.vedomosti.ru/technology/characters/2023/05/31/977789-bolshinstvo-nashih-partnerov-mudree-politikov. "В этом году мы фактически завершаем подготовительную серию экспериментов по отладке всех режимов ускорителя и масс-спектрометров для синтеза 120-го элемента. Научились получать высокие интенсивности ускоренного хрома и титана. Научились детектировать сверхтяжелые одиночные атомы в реакциях с минимальным сечением. Теперь ждем, когда закончится наработка материала для мишени на реакторах и сепараторах у наших партнеров в «Росатоме» и в США: кюрий, берклий, калифорний. Надеюсь, что в 2025 г. мы полноценно приступим к синтезу 120-го элемента."
- ↑ Chapman, Kit (10 October 2023). "Berkeley Lab to lead US hunt for element 120 after breakdown of collaboration with Russia". Chemistry World. https://www.chemistryworld.com/news/berkeley-lab-to-lead-us-hunt-for-element-120-after-breakdown-of-collaboration-with-russia/4018207.article.
- ↑ Biron, Lauren (16 October 2023). "Berkeley Lab to Test New Approach to Making Superheavy Elements". Lawrence Berkeley National Laboratory. https://physicalsciences.lbl.gov/2023/10/16/berkeley-lab-to-test-new-approach-to-making-superheavy-elements/.
- ↑ Biron, Lauren (23 July 2024). "A New Way to Make Element 116 Opens the Door to Heavier Atoms". Lawrence Berkeley National Laboratory. https://newscenter.lbl.gov/2024/07/23/a-new-way-to-make-element-116-opens-the-door-to-heavier-atoms/.
- ↑ Bourzac, Katherine (23 July 2024). "Heaviest element yet within reach after major breakthrough". Nature 632 (8023): 16–17. doi:10.1038/d41586-024-02416-3. PMID 39043946. Bibcode: 2024Natur.632...16B. https://www.nature.com/articles/d41586-024-02416-3. Retrieved 24 July 2024.
- ↑ Service, Robert F. (23 July 2024). "U.S. back in race to forge unknown, superheavy elements". Science. https://www.science.org/content/article/u-s-back-race-forge-unknown-superheavy-elements.
- ↑ Nelson, Felicity (15 August 2024). "How Japan Took the Lead in the Race to Discover Element 119". ACS Central Science 10 (9): 1669–1673. doi:10.1021/acscentsci.4c01266. PMID 39507239.
- ↑ Hofmann, Sigurd (2014). On Beyond Uranium: Journey to the End of the Periodic Table. CRC Press. p. 105. ISBN 978-0-415-28495-0. https://archive.org/details/onbeyonduraniumj0000hofm/page/105.
- ↑ 64.0 64.1 64.2 Karpov, A; Zagrebaev, V; Greiner, W (2015). "Superheavy Nuclei: which regions of nuclear map are accessible in the nearest studies". Texas A & M University. http://cyclotron.tamu.edu/she2015/assets/pdfs/presentations/Karpov_SHE_2015_TAMU.pdf.
- ↑ 65.0 65.1 see Flerov lab annual reports 2000–2004 inclusive http://www1.jinr.ru/Reports/Reports_eng_arh.html
- ↑ 66.0 66.1 Thomas, R.G.; Saxena, A.; Sahu, P.K.; Choudhury, R.K.; Govil, I.M.; Kailas, S.; Kapoor, S.S.; Barubi, M. et al. (2007). "Fission and binary fragmentation reactions in 80Se+208Pb and 80Se+232Th systems". Physical Review C 75 (2): 024604–1–024604–9. doi:10.1103/PhysRevC.75.024604.
- ↑ Lodhi, M.A.K., ed (March 1978). Superheavy Elements: Proceedings of the International Symposium on Superheavy Elements. Lubbock, Texas: Pergamon Press. ISBN 978-0-08-022946-1.
- ↑ Audi, G.; Kondev, F.G.; Wang, M.; Huang, W.J.; Naimi, S. (2017). "The NUBASE2016 evaluation of nuclear properties". Chinese Physics C 41 (3). doi:10.1088/1674-1137/41/3/030001. Bibcode: 2017ChPhC..41c0001A. http://amdc.in2p3.fr/nubase/2017Audi03.pdf. Retrieved 2018-12-08.
- ↑ 69.0 69.1 Marinov, A.; Rodushkin, I.; Kolb, D.; Pape, A.; Kashiv, Y.; Brandt, R.; Gentry, R. V.; Miller, H. W. (2010). "Evidence for a long-lived superheavy nucleus with atomic mass number A=292 and atomic number Z=~122 in natural Th". International Journal of Modern Physics E 19 (1): 131–140. doi:10.1142/S0218301310014662. Bibcode: 2010IJMPE..19..131M.
- ↑ Royal Society of Chemistry, "Heaviest element claim criticised ", Chemical World.
- ↑ 71.0 71.1 Marinov, A.; Rodushkin, I.; Kashiv, Y.; Halicz, L.; Segal, I.; Pape, A.; Gentry, R. V.; Miller, H. W. et al. (2007). "Existence of long-lived isomeric states in naturally-occurring neutron-deficient Th isotopes". Phys. Rev. C 76 (2): 021303(R). doi:10.1103/PhysRevC.76.021303. Bibcode: 2007PhRvC..76b1303M.
- ↑ R. C. Barber; J. R. De Laeter (2009). "Comment on 'Existence of long-lived isomeric states in naturally-occurring neutron-deficient Th isotopes'". Phys. Rev. C 79 (4). doi:10.1103/PhysRevC.79.049801. Bibcode: 2009PhRvC..79d9801B.
- ↑ A. Marinov; I. Rodushkin; Y. Kashiv; L. Halicz; I. Segal; A. Pape; R. V. Gentry; H. W. Miller et al. (2009). "Reply to "Comment on 'Existence of long-lived isomeric states in naturally-occurring neutron-deficient Th isotopes'"". Phys. Rev. C 79 (4). doi:10.1103/PhysRevC.79.049802. Bibcode: 2009PhRvC..79d9802M.
- ↑ J. Lachner; I. Dillmann; T. Faestermann; G. Korschinek; M. Poutivtsev; G. Rugel (2008). "Search for long-lived isomeric states in neutron-deficient thorium isotopes". Phys. Rev. C 78 (6). doi:10.1103/PhysRevC.78.064313. Bibcode: 2008PhRvC..78f4313L.
- ↑ Marinov, A.; Rodushkin, I.; Pape, A.; Kashiv, Y.; Kolb, D.; Brandt, R.; Gentry, R. V.; Miller, H. W. et al. (2009). "Existence of Long-Lived Isotopes of a Superheavy Element in Natural Au". International Journal of Modern Physics E 18 (3): 621–629. doi:10.1142/S021830130901280X. Bibcode: 2009IJMPE..18..621M. http://www.phys.huji.ac.il/~marinov/publications/Au_paper_IJMPE_73.pdf. Retrieved February 12, 2012.
- ↑ 76.0 76.1 Emsley, John (2011). Nature's Building Blocks: An A–Z Guide to the Elements (New ed.). New York: Oxford University Press. p. 592. ISBN 978-0-19-960563-7.
- ↑ Petermann, I; Langanke, K.; Martínez-Pinedo, G.; Panov, I.V; Reinhard, P.G.; Thielemann, F.K. (2012). "Have superheavy elements been produced in nature?". European Physical Journal A 48 (122): 122. doi:10.1140/epja/i2012-12122-6. Bibcode: 2012EPJA...48..122P. https://www.researchgate.net/publication/229156774.
- ↑ Jason Wright (16 March 2017). "Przybylski's Star III: Neutron Stars, Unbinilium, and aliens". https://sites.psu.edu/astrowright/2017/03/16/przybylskis-star-iii-neutron-stars-unbinilium-and-aliens/.
- ↑ V. A. Dzuba; V. V. Flambaum; J. K. Webb (2017). "Isotope shift and search for metastable superheavy elements in astrophysical data". Physical Review A 95 (6). doi:10.1103/PhysRevA.95.062515. Bibcode: 2017PhRvA..95f2515D.
- ↑ Archived at Ghostarchive and the Wayback Machine{{cbignore} b|url=https://www.youtube.com/watch?v=XKD0pFYewu4%7Ctitle=This Star Might Be Hiding Undiscovered Elements. Przybylski's Star|author=SciShow Space|website=youtube.com|date=31 July 2018|access-date=31 July 2018}}
- ↑ Waber, J. T. (1969). "SCF Dirac–Slater Calculations of the Translawrencium Elements". The Journal of Chemical Physics 51 (2): 664. doi:10.1063/1.1672054. Bibcode: 1969JChPh..51..664W.
- ↑ Amador, Davi H. T.; de Oliveira, Heibbe C. B.; Sambrano, Julio R.; Gargano, Ricardo; de Macedo, Luiz Guilherme M. (12 September 2016). "4-Component correlated all-electron study on Eka-actinium Fluoride (E121F) including Gaunt interaction: Accurate analytical form, bonding and influence on rovibrational spectra". Chemical Physics Letters 662: 169–175. doi:10.1016/j.cplett.2016.09.025. Bibcode: 2016CPL...662..169A.
- ↑ 83.00 83.01 83.02 83.03 83.04 83.05 83.06 83.07 83.08 83.09 83.10 83.11 83.12 Umemoto, Koichiro; Saito, Susumu (1996). "Electronic Configurations of Superheavy Elements". Journal of the Physical Society of Japan 65 (10): 3175–9. doi:10.1143/JPSJ.65.3175. Bibcode: 1996JPSJ...65.3175U. https://journals.jps.jp/doi/pdf/10.1143/JPSJ.65.3175. Retrieved 31 January 2021.
- ↑ 84.0 84.1 84.2 84.3 84.4 Dongon, J.P.; Pyykkö, P. (2017). "Chemistry of the 5g elements. Relativistic calculations on hexafluorides". Angewandte Chemie International Edition 56 (34): 10132–10134. doi:10.1002/anie.201701609. PMID 28444891. Bibcode: 2017ACIE...5610132D. https://hal-cea.archives-ouvertes.fr/cea-01515489/document.
- ↑ Jacoby, Mitch (2006). "As-yet-unsynthesized superheavy atom should form a stable diatomic molecule with fluorine". Chemical & Engineering News 84 (10): 19. doi:10.1021/cen-v084n010.p019a.
- ↑ Makhyoun, M. A. (October 1988). "On the electronic structure of 5g1 complexes of element 125: a quasi-relativistic MS-Xα study". Journal de Chimie Physique et de Physico-Chimie Biologique 85 (10): 917–24. doi:10.1051/jcp/1988850917. Bibcode: 1988JCP....85..917M.
- ↑ 87.0 87.1 87.2 Koura, H.; Chiba, S. (2013). "Single-Particle Levels of Spherical Nuclei in the Superheavy and Extremely Superheavy Mass Region". Journal of the Physical Society of Japan 82 (1). doi:10.7566/JPSJ.82.014201. Bibcode: 2013JPSJ...82a4201K. https://www.researchgate.net/publication/258799250.
- ↑ 88.0 88.1 "Nuclear scientists eye future landfall on a second 'island of stability'". 6 April 2008. http://www.eurekalert.org/pub_releases/2008-04/acs-nse031108.php.
- ↑ 89.0 89.1 Grumann, Jens; Mosel, Ulrich; Fink, Bernd; Greiner, Walter (1969). "Investigation of the stability of superheavy nuclei aroundZ=114 andZ=164". Zeitschrift für Physik 228 (5): 371–386. doi:10.1007/BF01406719. Bibcode: 1969ZPhy..228..371G.
- ↑ 90.0 90.1 90.2 Fricke, Burkhard (1977). "Dirac–Fock–Slater calculations for the elements Z = 100, fermium, to Z = 173". Recent Impact of Physics on Inorganic Chemistry 19: 83–192. doi:10.1016/0092-640X(77)90010-9. Bibcode: 1977ADNDT..19...83F. http://kobra.bibliothek.uni-kassel.de/bitstream/urn:nbn:de:hebis:34-2008071622807/1/Fricke_Dirac_1977.pdf. Retrieved 25 February 2016.
- ↑ 91.0 91.1 91.2 91.3 Eliav, Ephraim (26 April 2023). "Benchmark atomic electronic structures calculations at the edge of Periodic Table". JINR. https://indico.jinr.ru/event/3622/contributions/20027/attachments/15317/25832/Ephraim%20Eliav%20Yerevan-2023F.pptx.
- ↑ Penneman, R. A.; Mann, J. B.; Jørgensen, C. K. (February 1971). "Speculations on the chemistry of superheavy elements such as Z = 164". Chemical Physics Letters 8 (4): 321–326. doi:10.1016/0009-2614(71)80054-4. Bibcode: 1971CPL.....8..321P.
- ↑ Cwiok, S.; Heenen, P.-H.; Nazarewicz, W. (2005). "Shape coexistence and triaxiality in the superheavy nuclei". Nature 433 (7027): 705–9. doi:10.1038/nature03336. PMID 15716943. Bibcode: 2005Natur.433..705C.
- ↑ 94.0 94.1 Gambhir, Y. K.; Bhagwat, A.; Gupta, M. (2015). "The highest limiting Z in the extended periodic table". Journal of Physics G: Nuclear and Particle Physics 42 (12). doi:10.1088/0954-3899/42/12/125105. Bibcode: 2015JPhG...42l5105G. https://www.researchgate.net/publication/284213926.
- ↑ 95.0 95.1 Philip Ball (November 2010). "Would element 137 really spell the end of the periodic table? Philip Ball examines the evidence". Royal Society of Chemistry. https://www.chemistryworld.com/opinion/column-the-crucible/3005076.article.
- ↑ Eisberg, R.; Resnick, R. (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles. Wiley. ISBN 978-0-471-87373-0. https://archive.org/details/quantumphysicsof00eisb.
- ↑ "Solution of the Dirac Equation for Hydrogen". https://quantummechanics.ucsd.edu/ph130a/130_notes/node501.html.
- ↑ Bjorken, J. D.; Drell, S. D. (1964). Relativistic Quantum Mechanics. McGraw-Hill. https://archive.org/details/relativisticquan0000bjor.
- ↑ 99.0 99.1 99.2 99.3 Smits, O. R.; Indelicato, P.; Nazarewicz, W.; Piibeleht, M.; Schwerdtfeger, P. (2023). "Pushing the limits of the periodic table—A review on atomic relativistic electronic structure theory and calculations for the superheavy elements". Physics Reports 1035: 1–57. doi:10.1016/j.physrep.2023.09.004. Bibcode: 2023PhR..1035....1S.
- ↑ Greiner, W.; Schramm, S. (2008). "Resource Letter QEDV-1: The QED vacuum". American Journal of Physics 76 (6): 509. doi:10.1119/1.2820395. Bibcode: 2008AmJPh..76..509G., and references therein
- ↑ Wang, Yang; Wong, Dillon; Shytov, Andrey V.; Brar, Victor W.; Choi, Sangkook; Wu, Qiong; Tsai, Hsin-Zon; Regan, William et al. (May 10, 2013). "Observing Atomic Collapse Resonances in Artificial Nuclei on Graphene". Science 340 (6133): 734–737. doi:10.1126/science.1234320. PMID 23470728. Bibcode: 2013Sci...340..734W.
- ↑ Indelicato, Paul; Bieroń, Jacek; Jönsson, Per (2011-06-01). "Are MCDF calculations 101% correct in the super-heavy elements range?" (in en). Theoretical Chemistry Accounts 129 (3–5): 495–505. doi:10.1007/s00214-010-0887-3. ISSN 1432-881X. https://dspace.mah.se/handle/2043/12984.
- ↑ Reinhardt, Joachim; Greiner, Walter (2015). "Probing Supercritical Fields with Real and with Artificial Nuclei". Nuclear Physics: Present and Future. pp. 195–210. doi:10.1007/978-3-319-10199-6_19. ISBN 978-3-319-10198-9.
- ↑ 104.0 104.1 Giuliani, S. A.; Matheson, Z.; Nazarewicz, W.; Olsen, E.; Reinhard, P.-G.; Sadhukhan, J.; Schtruempf, B.; Schunck, N. et al. (2019). "Colloquium: Superheavy elements: Oganesson and beyond". Reviews of Modern Physics 91 (1): 011001-1–011001-25. doi:10.1103/RevModPhys.91.011001. Bibcode: 2019RvMP...91a1001G.
- ↑ Holdom, B.; Ren, J.; Zhang, C. (2018). "Quark matter may not be strange". Physical Review Letters 120 (1): 222001-1–222001-6. doi:10.1103/PhysRevLett.120.222001. PMID 29906186. Bibcode: 2018PhRvL.120v2001H.
- ↑ Cheng-Jun, Xia; She-Sheng, Xue; Ren-Xin, Xu; Shan-Gui, Zhou (2020). "Supercritically charged objects and electron-positron pair creation". Physical Review D 101 (10). doi:10.1103/PhysRevD.101.103031. Bibcode: 2020PhRvD.101j3031X.
- ↑ Marcillac, Pierre de; Noël Coron; Gérard Dambier; Jacques Leblanc; Jean-Pierre Moalic (April 2003). "Experimental detection of α-particles from the radioactive decay of natural bismuth". Nature 422 (6934): 876–878. doi:10.1038/nature01541. PMID 12712201. Bibcode: 2003Natur.422..876D.
- ↑ Considine, Glenn D.; Kulik, Peter H. (2002). Van Nostrand's scientific encyclopedia (9 ed.). Wiley-Interscience. ISBN 978-0-471-33230-5. OCLC 223349096.
- ↑ 109.0 109.1 109.2 109.3 Koura, H. (2011). "Decay modes and a limit of existence of nuclei in the superheavy mass region". 4th International Conference on the Chemistry and Physics of the Transactinide Elements. http://tan11.jinr.ru/pdf/10_Sep/S_2/05_Koura.pdf. Retrieved 18 November 2018.
- ↑ 110.0 110.1 Greiner, W. (2013). "Nuclei: superheavy-superneutronic-strange-and of antimatter". Journal of Physics: Conference Series 413 (1). doi:10.1088/1742-6596/413/1/012002. Bibcode: 2013JPhCS.413a2002G. http://inspirehep.net/record/1221632/files/jpconf13_413_012002.pdf.
- ↑ 111.0 111.1 Denisov, V. (2005). "Magic numbers of ultraheavy nuclei". Physics of Atomic Nuclei 68 (7): 1133–1137. doi:10.1134/1.1992567. Bibcode: 2005PAN....68.1133D. https://www.researchgate.net/publication/225734594.
- ↑ Schwerdtfeger, Peter; Pašteka, Lukáš F.; Punnett, Andrew; Bowman, Patrick O. (2015). "Relativistic and quantum electrodynamic effects in superheavy elements". Nuclear Physics A 944 (December 2015): 551–577. doi:10.1016/j.nuclphysa.2015.02.005. Bibcode: 2015NuPhA.944..551S.
- ↑ Dvorak, J.; Brüchle, W.; Chelnokov, M.; Dressler, R.; Düllmann, Ch. E.; Eberhardt, K.; Gorshkov, V.; Jäger, E. et al. (2006). "Doubly Magic Nucleus 108270Hs162". Physical Review Letters 97 (24). doi:10.1103/PhysRevLett.97.242501. PMID 17280272. Bibcode: 2006PhRvL..97x2501D. https://www.dora.lib4ri.ch/psi/islandora/object/psi%3A16351.
- ↑ LaForge, Evan; Price, Will; Rafelski, Johann (15 September 2023). "Superheavy elements and ultradense matter". The European Physical Journal Plus 138 (9): 812. doi:10.1140/epjp/s13360-023-04454-8. Bibcode: 2023EPJP..138..812L.
- ↑ "Physicists are pushing the periodic table to its limits | Science News". 27 February 2019. https://www.sciencenews.org/article/physics-periodic-table-future-superheavy-elements.
- ↑ Dechargé, J.; Berger, J.-F.; Girod, M.; Dietrich, K. (March 2003). "Bubbles and semi-bubbles as a new kind of superheavy nuclei". Nuclear Physics A 716: 55–86. doi:10.1016/S0375-9474(02)01398-2. Bibcode: 2003NuPhA.716...55D.
- ↑ Agbemava, S. E.; Afanasjev, A. V. (25 March 2021). "Hyperheavy spherical and toroidal nuclei: The role of shell structure". Physical Review C 103 (3). doi:10.1103/PhysRevC.103.034323. Bibcode: 2021PhRvC.103c4323A.
- ↑ Afanasjev, A.V.; Agbemava, S.E.; Gyawali, A. (July 2018). "Hyperheavy nuclei: Existence and stability". Physics Letters B 782: 533–540. doi:10.1016/j.physletb.2018.05.070. Bibcode: 2018PhLB..782..533A.
- ↑ Palenzuela, Y. M.; Ruiz, L. F.; Karpov, A.; Greiner, W. (2012). "Systematic Study of Decay Properties of Heaviest Elements". Bulletin of the Russian Academy of Sciences: Physics 76 (11): 1165–1171. doi:10.3103/S1062873812110172. ISSN 1062-8738. Bibcode: 2012BRASP..76.1165P. http://nrv.jinr.ru/karpov/publications/Palenzuela12_BRAS.pdf. Retrieved 2018-12-01.
- ↑ Poenaru, Dorin N.; Gherghescu, R. A.; Greiner, W. (2012). "Cluster decay of superheavy nuclei". Physical Review C 85 (3). doi:10.1103/PhysRevC.85.034615. Bibcode: 2012PhRvC..85c4615P. https://www.researchgate.net/publication/235507943. Retrieved 2 May 2017.
- ↑ 121.0 121.1 121.2 121.3 van der Schoor, K. (2016). Electronic structure of element 123 (PDF) (Thesis). Rijksuniversiteit Groningen.
- ↑ Indelicato, Paul; Bieroń, Jacek; Jönsson, Per (2011). "Are MCDF calculations 101% correct in the super-heavy elements range?". Theoretical Chemistry Accounts 129 (3–5): 495–505. doi:10.1007/s00214-010-0887-3. https://link.springer.com/article/10.1007/s00214-010-0887-3.
- ↑ 123.00 123.01 123.02 123.03 123.04 123.05 123.06 123.07 123.08 123.09 123.10 123.11 123.12 123.13 123.14 123.15 123.16 123.17 123.18 123.19 123.20 123.21 123.22 123.23 123.24 123.25 123.26 123.27 123.28 123.29 123.30 123.31 123.32 123.33 123.34 123.35 123.36 123.37 123.38 123.39 123.40 123.41 123.42 123.43 123.44 123.45 123.46 123.47 123.48 123.49 "Feasible electron configurations up to Z = 172". http://www.primefan.ru/stuff/chem/ptable/ptable.html.
Further reading
- Kaldor, U. (2005). "Superheavy Elements—Chemistry and Spectroscopy". Encyclopedia of Computational Chemistry. doi:10.1002/0470845015.cu0044. ISBN 978-0-470-84501-1.
- Seaborg, G. T. (1968). "Elements Beyond 100, Present Status and Future Prospects". Annual Review of Nuclear Science 18: 53–152. doi:10.1146/annurev.ns.18.120168.000413. Bibcode: 1968ARNPS..18...53S.
- Scerri, Eric. (2011). A Very Short Introduction to the Periodic Table, Oxford University Press, Oxford. OUP Oxford. ISBN 978-0-19-958249-5.
External links
- Holler, Jim. "Images of g-orbitals". University of Kentucky. http://www.uky.edu/~holler/html/g.html.
- Rihani, Jeries A.. "The extended periodic table of the elements". http://jeries.rihani.com/.
- Scerri, Eric. "Eric Scerri's website for the elements and the periodic table". https://www.ericscerri.com.
- From a page move: This is a redirect from a page that has been moved (renamed). This page was kept as a redirect to avoid breaking links, both internal and external, that may have been made to the old page name.
 |
 KSF
KSF