Cocoloring

Cocoloring with 3 colors (upper left figure): a proper 3-coloring of this graph is impossible. The blue subgraph forms a clique (bottom right figure), while the red and green subgraphs form cliques on the graph's complement.

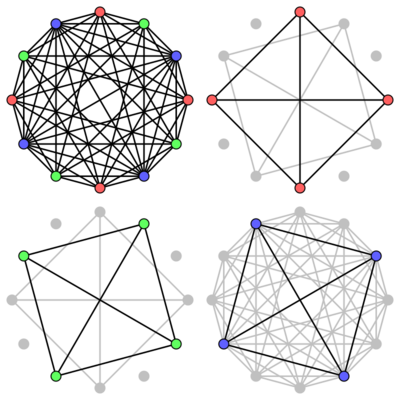
In graph theory, a cocoloring of a graph G is an assignment of colors to the vertices such that each color class forms an independent set in G or in the complement of G. The cochromatic number z(G) of G is the fewest colors needed in any cocolorings of G. The graphs with cochromatic number 2 are exactly the bipartite graphs, complements of bipartite graphs, and split graphs.

As the requirement that each color class be a clique or independent is weaker than the requirement for coloring (in which each color class must be an independent set) and stronger than for subcoloring (in which each color class must be a disjoint union of cliques), it follows that the cochromatic number of G is less than or equal to the chromatic number of G, and that it is greater than or equal to the subchromatic number of G.

Cocoloring was named and first studied by (Lesniak Straight). (Jørgensen 1995) characterizes critical 3-cochromatic graphs, while (Fomin Kratsch) describe algorithms for approximating the cochromatic number of a graph. (Zverovich 2000) defines a class of perfect cochromatic graphs, analogous to the definition of perfect graphs via graph coloring, and provides a forbidden subgraph characterization of these graphs.

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Cocoloring. Read more