Covering space

Intuitively, a covering locally projects a "stack of pancakes" above an open neighborhood [math]\displaystyle{ U }[/math] onto [math]\displaystyle{ U }[/math]

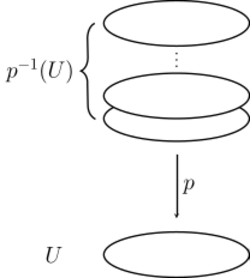
In topology, a covering or covering projection is a surjective map between topological spaces that, intuitively, locally acts like a projection of multiple copies of a space onto itself. In particular, coverings are special types of local homeomorphisms. If [math]\displaystyle{ p : \tilde X \to X }[/math] is a covering, [math]\displaystyle{ (\tilde X, p) }[/math] is said to be a covering space or cover of [math]\displaystyle{ X }[/math], and [math]\displaystyle{ X }[/math] is said to be the base of the covering, or simply the base. By abuse of terminology, [math]\displaystyle{ \tilde X }[/math] and [math]\displaystyle{ p }[/math] may sometimes be called covering spaces as well. Since coverings are local homeomorphisms, a covering space is a special kind of étale space.

Covering spaces first arose in the context of complex analysis (specifically, the technique of analytic continuation), where they were introduced by Riemann as domains on which naturally multivalued complex functions become single-valued. These spaces are now called Riemann surfaces.^[1]:{{{1}}}

Covering spaces are an important tool in several areas of mathematics. In modern geometry, covering spaces (or branched coverings, which have slightly weaker conditions) are used in the construction of manifolds, orbifolds, and the morphisms between them. In algebraic topology, covering spaces are closely related to the fundamental group: for one, since all coverings have the homotopy lifting property, covering spaces are an important tool in the calculation of homotopy groups. A standard example in this vein is the calculation of the fundamental group of the circle by means of the covering of [math]\displaystyle{ S^1 }[/math] by [math]\displaystyle{ \mathbb{R} }[/math] (see below).^[2]:{{{1}}} Under certain conditions, covering spaces also exhibit a Galois correspondance with the subgroups of the fundamental group.

Definition

Let [math]\displaystyle{ X }[/math] be a topological space. A covering of [math]\displaystyle{ X }[/math] is a continuous map

[math]\displaystyle{ \pi : \tilde X \rightarrow X }[/math]

such that for every [math]\displaystyle{ x \in X }[/math] there exists an open neighborhood [math]\displaystyle{ U_x }[/math] of [math]\displaystyle{ x }[/math] and a discrete space [math]\displaystyle{ D_x }[/math] such that [math]\displaystyle{ \pi^{-1}(U_x)= \displaystyle \bigsqcup_{d \in D_x} V_d }[/math] and [math]\displaystyle{ \pi|_{V_d}:V_d \rightarrow U_x }[/math] is a homeomorphism for every [math]\displaystyle{ d \in D_x }[/math]. The open sets [math]\displaystyle{ V_{d} }[/math] are called sheets, which are uniquely determined up to homeomorphism if [math]\displaystyle{ U_x }[/math] is connected.^[2]:56 For each [math]\displaystyle{ x \in X }[/math] the discrete set [math]\displaystyle{ \pi^{-1}(x) }[/math] is called the fiber of [math]\displaystyle{ x }[/math]. If [math]\displaystyle{ X }[/math] is connected, it can be shown that the cardinality of [math]\displaystyle{ D_x }[/math] is the same for all [math]\displaystyle{ x \in X }[/math]; this value is called the degree of the covering. If [math]\displaystyle{ \tilde X }[/math] is path-connected, then the covering [math]\displaystyle{ \pi : \tilde X \rightarrow X }[/math] is called a path-connected covering. This definition is equivalent to the statement that [math]\displaystyle{ p }[/math] is a locally trivial Fiber bundle.

Examples

• For every topological space [math]\displaystyle{ X }[/math], the identity map [math]\displaystyle{ \operatorname{id}:X \rightarrow X }[/math] is a covering. Likewise for any discrete space [math]\displaystyle{ D }[/math] the projection [math]\displaystyle{ \pi:X \times D \rightarrow X }[/math] taking [math]\displaystyle{ (x, i) \mapsto x }[/math] is a covering. Coverings of this type are called trivial coverings; if [math]\displaystyle{ D }[/math] has finitely many (say [math]\displaystyle{ k }[/math]) elements, the covering is called the trivial [math]\displaystyle{ k }[/math]-sheeted covering of [math]\displaystyle{ X }[/math].

The space [math]\displaystyle{ Y=[0,1] \times \mathbb{R} }[/math] is a covering space of [math]\displaystyle{ X=[0,1] \times S^1 }[/math]. The disjoint open sets [math]\displaystyle{ S_i }[/math] are mapped homeomorphically onto [math]\displaystyle{ U }[/math]. The fiber of [math]\displaystyle{ x }[/math] consists of the points [math]\displaystyle{ y_i }[/math].

• The map [math]\displaystyle{ r : \mathbb{R} \to S^1 }[/math] with [math]\displaystyle{ r(t)=(\cos(2 \pi t), \sin(2 \pi t)) }[/math] is a covering of the unit circle [math]\displaystyle{ S^1 }[/math]. The base of the covering is [math]\displaystyle{ S^1 }[/math] and the covering space is [math]\displaystyle{ \mathbb{R} }[/math]. For any point [math]\displaystyle{ x = (x_1, x_2) \in S^1 }[/math] such that [math]\displaystyle{ x_1 \gt 0 }[/math], the set [math]\displaystyle{ U := \{(x_1, x_2) \in S^1 \mid x_1 \gt 0 \} }[/math] is an open neighborhood of [math]\displaystyle{ x }[/math]. The preimage of [math]\displaystyle{ U }[/math] under [math]\displaystyle{ r }[/math] is

  [math]\displaystyle{ r^{-1}(U)=\displaystyle\bigsqcup_{n \in \mathbb{Z}} \left( n - \frac 1 4, n + \frac 1 4\right) }[/math]

and the sheets of the covering are [math]\displaystyle{ V_n = (n - 1/4, n+1/4) }[/math] for [math]\displaystyle{ n \in \mathbb{Z}. }[/math] The fiber of [math]\displaystyle{ x }[/math] is

[math]\displaystyle{ r^{-1}(x) = \{t \in \mathbb{R} \mid (\cos(2 \pi t), \sin(2 \pi t)) = x\}. }[/math]

• Another covering of the unit circle is the map [math]\displaystyle{ q : S^1 \to S^1 }[/math] with [math]\displaystyle{ q(z)=z^{n} }[/math] for some [math]\displaystyle{ n \in \mathbb{N}. }[/math] For an open neighborhood [math]\displaystyle{ U }[/math] of an [math]\displaystyle{ x \in S^1 }[/math], one has:

[math]\displaystyle{ q^{-1}(U)=\displaystyle\bigsqcup_{i=1}^{n} U }[/math].

• A map which is a local homeomorphism but not a covering of the unit circle is [math]\displaystyle{ p : \mathbb{R_{+}} \to S^1 }[/math] with [math]\displaystyle{ p(t)=(\cos(2 \pi t), \sin(2 \pi t)) }[/math]. There is a sheet of an open neighborhood of [math]\displaystyle{ (1,0) }[/math], which is not mapped homeomorphically onto [math]\displaystyle{ U }[/math].

Properties

Local homeomorphism

Since a covering [math]\displaystyle{ \pi:E \rightarrow X }[/math] maps each of the disjoint open sets of [math]\displaystyle{ \pi^{-1}(U) }[/math] homeomorphically onto [math]\displaystyle{ U }[/math] it is a local homeomorphism, i.e. [math]\displaystyle{ \pi }[/math] is a continuous map and for every [math]\displaystyle{ e \in E }[/math] there exists an open neighborhood [math]\displaystyle{ V \subset E }[/math] of [math]\displaystyle{ e }[/math], such that [math]\displaystyle{ \pi|_V : V \rightarrow \pi(V) }[/math] is a homeomorphism.

It follows that the covering space [math]\displaystyle{ E }[/math] and the base space [math]\displaystyle{ X }[/math] locally share the same properties.

• If [math]\displaystyle{ X }[/math] is a connected and non-orientable manifold, then there is a covering [math]\displaystyle{ \pi:\tilde X \rightarrow X }[/math] of degree [math]\displaystyle{ 2 }[/math], whereby [math]\displaystyle{ \tilde X }[/math] is a connected and orientable manifold.^[2]:234
• If [math]\displaystyle{ X }[/math] is a connected Lie group, then there is a covering [math]\displaystyle{ \pi:\tilde X \rightarrow X }[/math] which is also a Lie group homomorphism and [math]\displaystyle{ \tilde X := \{\gamma:\gamma \text{ is a path in X with }\gamma(0)= \boldsymbol{1_X} \text{ modulo homotopy with fixed ends}\} }[/math] is a Lie group.^[3]:{{{1}}}
• If [math]\displaystyle{ X }[/math] is a graph, then it follows for a covering [math]\displaystyle{ \pi:E \rightarrow X }[/math] that [math]\displaystyle{ E }[/math] is also a graph.^[2]:85
• If [math]\displaystyle{ X }[/math] is a connected manifold, then there is a covering [math]\displaystyle{ \pi:\tilde X \rightarrow X }[/math], whereby [math]\displaystyle{ \tilde X }[/math] is a connected and simply connected manifold.^[4]:32
• If [math]\displaystyle{ X }[/math] is a connected Riemann surface, then there is a covering [math]\displaystyle{ \pi:\tilde X \rightarrow X }[/math] which is also a holomorphic map^[4]:22 and [math]\displaystyle{ \tilde X }[/math] is a connected and simply connected Riemann surface.^[4]:32

Factorisation

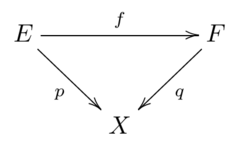
Let [math]\displaystyle{ X, Y }[/math] and [math]\displaystyle{ E }[/math] be path-connected, locally path-connected spaces, and [math]\displaystyle{ p,q }[/math] and [math]\displaystyle{ r }[/math] be continuous maps, such that the diagram

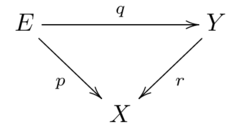
commutes.

• If [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] are coverings, so is [math]\displaystyle{ r }[/math].
• If [math]\displaystyle{ p }[/math] and [math]\displaystyle{ r }[/math] are coverings, so is [math]\displaystyle{ q }[/math].^[5]:485

Product of coverings

Let [math]\displaystyle{ X }[/math] and [math]\displaystyle{ X' }[/math] be topological spaces and [math]\displaystyle{ p:E \rightarrow X }[/math] and [math]\displaystyle{ p':E' \rightarrow X' }[/math] be coverings, then [math]\displaystyle{ p \times p':E \times E' \rightarrow X \times X' }[/math] with [math]\displaystyle{ (p \times p')(e, e') = (p(e), p'(e')) }[/math] is a covering.^[5]:{{{1}}} However covering of [math]\displaystyle{ X\times X' }[/math] are not all of this form in general.

Equivalence of coverings

Let [math]\displaystyle{ X }[/math] be a topological space and [math]\displaystyle{ p:E \rightarrow X }[/math] and [math]\displaystyle{ p':E' \rightarrow X }[/math] be coverings. Both coverings are called equivalent, if there exists a homeomorphism [math]\displaystyle{ h:E \rightarrow E' }[/math], such that the diagram

commutes. If such a homeomorphism exists, then one calls the covering spaces [math]\displaystyle{ E }[/math] and [math]\displaystyle{ E' }[/math] isomorphic.

Lifting property

All coverings satisfy the lifting property, i.e.:

Let [math]\displaystyle{ I }[/math] be the unit interval and [math]\displaystyle{ p:E \rightarrow X }[/math] be a covering. Let [math]\displaystyle{ F:Y \times I \rightarrow X }[/math] be a continuous map and [math]\displaystyle{ \tilde F_0:Y \times \{0\} \rightarrow E }[/math] be a lift of [math]\displaystyle{ F|_{Y \times \{0\}} }[/math], i.e. a continuous map such that [math]\displaystyle{ p \circ \tilde F_0 = F|_{Y \times \{0\}} }[/math]. Then there is a uniquely determined, continuous map [math]\displaystyle{ \tilde F:Y \times I \rightarrow E }[/math] for which [math]\displaystyle{ \tilde F(y,0) = \tilde F_0 }[/math] and which is a lift of [math]\displaystyle{ F }[/math], i.e. [math]\displaystyle{ p \circ \tilde F = F }[/math].^[2]:60

If [math]\displaystyle{ X }[/math] is a path-connected space, then for [math]\displaystyle{ Y=\{0\} }[/math] it follows that the map [math]\displaystyle{ \tilde F }[/math] is a lift of a path in [math]\displaystyle{ X }[/math] and for [math]\displaystyle{ Y=I }[/math] it is a lift of a homotopy of paths in [math]\displaystyle{ X }[/math].

As a consequence, one can show that the fundamental group [math]\displaystyle{ \pi_{1}(S^1) }[/math] of the unit circle is an infinite cyclic group, which is generated by the homotopy classes of the loop [math]\displaystyle{ \gamma: I \rightarrow S^1 }[/math] with [math]\displaystyle{ \gamma (t) = (\cos(2 \pi t), \sin(2 \pi t)) }[/math].^[2]:29

Let [math]\displaystyle{ X }[/math] be a path-connected space and [math]\displaystyle{ p:E \rightarrow X }[/math] be a connected covering. Let [math]\displaystyle{ x,y \in X }[/math] be any two points, which are connected by a path [math]\displaystyle{ \gamma }[/math], i.e. [math]\displaystyle{ \gamma(0)= x }[/math] and [math]\displaystyle{ \gamma(1)= y }[/math]. Let [math]\displaystyle{ \tilde \gamma }[/math] be the unique lift of [math]\displaystyle{ \gamma }[/math], then the map

[math]\displaystyle{ L_{\gamma}:p^{-1}(x) \rightarrow p^{-1}(y) }[/math] with [math]\displaystyle{ L_{\gamma}(\tilde \gamma (0))=\tilde \gamma (1) }[/math]

is bijective.^[2]:69

If [math]\displaystyle{ X }[/math] is a path-connected space and [math]\displaystyle{ p: E \rightarrow X }[/math] a connected covering, then the induced group homomorphism

[math]\displaystyle{ p_{\#}: \pi_{1}(E) \rightarrow \pi_{1}(X) }[/math] with [math]\displaystyle{ p_{\#}([\gamma])=[p \circ \gamma] }[/math],

is injective and the subgroup [math]\displaystyle{ p_{\#}(\pi_1(E)) }[/math] of [math]\displaystyle{ \pi_1(X) }[/math] consists of the homotopy classes of loops in [math]\displaystyle{ X }[/math], whose lifts are loops in [math]\displaystyle{ E }[/math].^[2]:61

Branched covering

Definitions

Holomorphic maps between Riemann surfaces

Let [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] be Riemann surfaces, i.e. one dimensional complex manifolds, and let [math]\displaystyle{ f: X \rightarrow Y }[/math] be a continuous map. [math]\displaystyle{ f }[/math] is holomorphic in a point [math]\displaystyle{ x \in X }[/math], if for any charts [math]\displaystyle{ \phi _x:U_1 \rightarrow V_1 }[/math] of [math]\displaystyle{ x }[/math] and [math]\displaystyle{ \phi_{f(x)}:U_2 \rightarrow V_2 }[/math] of [math]\displaystyle{ f(x) }[/math], with [math]\displaystyle{ \phi_x(U_1) \subset U_2 }[/math], the map [math]\displaystyle{ \phi _{f(x)} \circ f \circ \phi^{-1} _x: \mathbb{C} \rightarrow \mathbb{C} }[/math] is holomorphic.

If [math]\displaystyle{ f }[/math] is holomorphic at all [math]\displaystyle{ x \in X }[/math], we say [math]\displaystyle{ f }[/math] is holomorphic.

The map [math]\displaystyle{ F =\phi _{f(x)} \circ f \circ \phi^{-1} _x }[/math] is called the local expression of [math]\displaystyle{ f }[/math] in [math]\displaystyle{ x \in X }[/math].

If [math]\displaystyle{ f: X \rightarrow Y }[/math] is a non-constant, holomorphic map between compact Riemann surfaces, then [math]\displaystyle{ f }[/math] is surjective and an open map,^[4]:{{{1}}} i.e. for every open set [math]\displaystyle{ U \subset X }[/math] the image [math]\displaystyle{ f(U) \subset Y }[/math] is also open.

Ramification point and branch point

Let [math]\displaystyle{ f: X \rightarrow Y }[/math] be a non-constant, holomorphic map between compact Riemann surfaces. For every [math]\displaystyle{ x \in X }[/math] there exist charts for [math]\displaystyle{ x }[/math] and [math]\displaystyle{ f(x) }[/math] and there exists a uniquely determined [math]\displaystyle{ k_x \in \mathbb{N_{\gt 0}} }[/math], such that the local expression [math]\displaystyle{ F }[/math] of [math]\displaystyle{ f }[/math] in [math]\displaystyle{ x }[/math] is of the form [math]\displaystyle{ z \mapsto z^{k_{x}} }[/math].^[4]:10 The number [math]\displaystyle{ k_x }[/math] is called the ramification index of [math]\displaystyle{ f }[/math] in [math]\displaystyle{ x }[/math] and the point [math]\displaystyle{ x \in X }[/math] is called a ramification point if [math]\displaystyle{ k_x \geq 2 }[/math]. If [math]\displaystyle{ k_x =1 }[/math] for an [math]\displaystyle{ x \in X }[/math], then [math]\displaystyle{ x }[/math] is unramified. The image point [math]\displaystyle{ y=f(x) \in Y }[/math] of a ramification point is called a branch point.

Degree of a holomorphic map

Let [math]\displaystyle{ f: X \rightarrow Y }[/math] be a non-constant, holomorphic map between compact Riemann surfaces. The degree [math]\displaystyle{ \operatorname{deg}(f) }[/math] of [math]\displaystyle{ f }[/math] is the cardinality of the fiber of an unramified point [math]\displaystyle{ y=f(x) \in Y }[/math], i.e. [math]\displaystyle{ \operatorname{deg}(f):=|f^{-1}(y)| }[/math].

This number is well-defined, since for every [math]\displaystyle{ y \in Y }[/math] the fiber [math]\displaystyle{ f^{-1}(y) }[/math] is discrete^[4]:20 and for any two unramified points [math]\displaystyle{ y_1,y_2 \in Y }[/math], it is: [math]\displaystyle{ |f^{-1}(y_1)|=|f^{-1}(y_2)|. }[/math]

It can be calculated by:

[math]\displaystyle{ \sum_{x \in f^{-1}(y)} k_x = \operatorname{deg}(f) }[/math] ^[4]:29

Branched covering

Definition

A continuous map [math]\displaystyle{ f: X \rightarrow Y }[/math] is called a branched covering, if there exists a closed set with dense complement [math]\displaystyle{ E \subset Y }[/math], such that [math]\displaystyle{ f_{|X \smallsetminus f^{-1}(E)}:X \smallsetminus f^{-1}(E) \rightarrow Y \smallsetminus E }[/math] is a covering.

Examples

• Let [math]\displaystyle{ n \in \mathbb{N} }[/math] and [math]\displaystyle{ n \geq 2 }[/math], then [math]\displaystyle{ f:\mathbb{C} \rightarrow \mathbb{C} }[/math] with [math]\displaystyle{ f(z)=z^n }[/math] is branched covering of degree [math]\displaystyle{ n }[/math], where by [math]\displaystyle{ z=0 }[/math] is a branch point.
• Every non-constant, holomorphic map between compact Riemann surfaces [math]\displaystyle{ f: X \rightarrow Y }[/math] of degree [math]\displaystyle{ d }[/math] is a branched covering of degree [math]\displaystyle{ d }[/math].

Universal covering

Definition

Let [math]\displaystyle{ p: \tilde X \rightarrow X }[/math] be a simply connected covering. If [math]\displaystyle{ \beta : E \rightarrow X }[/math] is another simply connected covering, then there exists a uniquely determined homeomorphism [math]\displaystyle{ \alpha : \tilde X \rightarrow E }[/math], such that the diagram

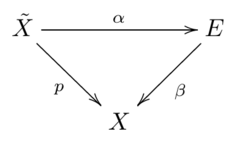
commutes.^[5]:482

This means that [math]\displaystyle{ p }[/math] is, up to equivalence, uniquely determined and because of that universal property denoted as the universal covering of the space [math]\displaystyle{ X }[/math].

Existence

A universal covering does not always exist, but the following properties guarantee its existence:

Let [math]\displaystyle{ X }[/math] be a connected, locally simply connected topological space; then, there exists a universal covering [math]\displaystyle{ p:\tilde X \rightarrow X }[/math].

[math]\displaystyle{ \tilde X }[/math] is defined as [math]\displaystyle{ \tilde X := \{\gamma:\gamma \text{ is a path in }X \text{ with }\gamma(0) = x_0 \}/\text{ homotopy with fixed ends} }[/math] and [math]\displaystyle{ p:\tilde X \rightarrow X }[/math] by [math]\displaystyle{ p([\gamma]):=\gamma(1) }[/math].^[2]:64

The topology on [math]\displaystyle{ \tilde X }[/math] is constructed as follows: Let [math]\displaystyle{ \gamma:I \rightarrow X }[/math] be a path with [math]\displaystyle{ \gamma(0)=x_0 }[/math]. Let [math]\displaystyle{ U }[/math] be a simply connected neighborhood of the endpoint [math]\displaystyle{ x=\gamma(1) }[/math], then for every [math]\displaystyle{ y \in U }[/math] the paths [math]\displaystyle{ \sigma_y }[/math] inside [math]\displaystyle{ U }[/math] from [math]\displaystyle{ x }[/math] to [math]\displaystyle{ y }[/math] are uniquely determined up to homotopy. Now consider [math]\displaystyle{ \tilde U:=\{\gamma.\sigma_y:y \in U \}/\text{ homotopy with fixed ends} }[/math], then [math]\displaystyle{ p_{|\tilde U}: \tilde U \rightarrow U }[/math] with [math]\displaystyle{ p([\gamma.\sigma_y])=\gamma.\sigma_y(1)=y }[/math] is a bijection and [math]\displaystyle{ \tilde U }[/math] can be equipped with the final topology of [math]\displaystyle{ p_{|\tilde U} }[/math].

The fundamental group [math]\displaystyle{ \pi_{1}(X,x_0) = \Gamma }[/math] acts freely through [math]\displaystyle{ ([\gamma],[\tilde x]) \mapsto [\gamma.\tilde x] }[/math] on [math]\displaystyle{ \tilde X }[/math] and [math]\displaystyle{ \psi:\Gamma \backslash \tilde X \rightarrow X }[/math] with [math]\displaystyle{ \psi([\Gamma \tilde x])=\tilde x(1) }[/math] is a homeomorphism, i.e. [math]\displaystyle{ \Gamma \backslash \tilde X \cong X }[/math].

Examples

The Hawaiian earring. Only the ten largest circles are shown.

• [math]\displaystyle{ r : \mathbb{R} \to S^1 }[/math] with [math]\displaystyle{ r(t)=(\cos(2 \pi t), \sin(2 \pi t)) }[/math] is the universal covering of the unit circle [math]\displaystyle{ S^1 }[/math].
• [math]\displaystyle{ p : S^n \to \mathbb{R}P^n \cong \{+1,-1\}\backslash S^n }[/math] with [math]\displaystyle{ p(x)=[x] }[/math] is the universal covering of the projective space [math]\displaystyle{ \mathbb{R}P^n }[/math] for [math]\displaystyle{ n\gt 1 }[/math].
• [math]\displaystyle{ q : \mathrm{SU}(n) \ltimes \mathbb{R} \to U(n) }[/math] with [math]\displaystyle{ q(A,t)= \begin{bmatrix} \exp(2 \pi i t) & 0\\ 0 & I_{n-1} \end{bmatrix}_\vphantom{x} A }[/math] is the universal covering of the unitary group [math]\displaystyle{ U(n) }[/math].^{[6](Theorem 1)}
• Since [math]\displaystyle{ \mathrm{SU}(2) \cong S^3 }[/math], it follows that the quotient map [math]\displaystyle{ f : \mathrm{SU}(2) \rightarrow \mathrm{SU}(2) \backslash \mathbb{Z_2} \cong \mathrm{SO}(3) }[/math] is the universal covering of the [math]\displaystyle{ \mathrm{SO}(3) }[/math].
• A topological space which has no universal covering is the Hawaiian earring: [math]\displaystyle{ X = \bigcup_{n\in \N}\left\{(x_1,x_2)\in\R^{2} : \Bigl(x_1-\frac{1}{n}\Bigr)^2+x_2^2=\frac{1}{n^2}\right\} }[/math] One can show that no neighborhood of the origin [math]\displaystyle{ (0,0) }[/math] is simply connected.^[5]:487

G-coverings

Let G be a discrete group acting on the topological space X. This means that each element g of G is associated to a homeomorphism H_g of X onto itself, in such a way that H_{g h} is always equal to H_g ∘ H_h for any two elements g and h of G. (Or in other words, a group action of the group G on the space X is just a group homomorphism of the group G into the group Homeo(X) of self-homeomorphisms of X.) It is natural to ask under what conditions the projection from X to the orbit space X/G is a covering map. This is not always true since the action may have fixed points. An example for this is the cyclic group of order 2 acting on a product X × X by the twist action where the non-identity element acts by (x, y) ↦ (y, x). Thus the study of the relation between the fundamental groups of X and X/G is not so straightforward.

However the group G does act on the fundamental groupoid of X, and so the study is best handled by considering groups acting on groupoids, and the corresponding orbit groupoids. The theory for this is set down in Chapter 11 of the book Topology and groupoids referred to below. The main result is that for discontinuous actions of a group G on a Hausdorff space X which admits a universal cover, then the fundamental groupoid of the orbit space X/G is isomorphic to the orbit groupoid of the fundamental groupoid of X, i.e. the quotient of that groupoid by the action of the group G. This leads to explicit computations, for example of the fundamental group of the symmetric square of a space.

Deck transformation

Definition

Let [math]\displaystyle{ p:E \rightarrow X }[/math] be a covering. A deck transformation is a homeomorphism [math]\displaystyle{ d:E \rightarrow E }[/math], such that the diagram of continuous maps

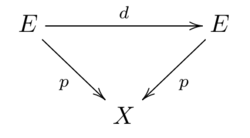
commutes. Together with the composition of maps, the set of deck transformation forms a group [math]\displaystyle{ \operatorname{Deck}(p) }[/math], which is the same as [math]\displaystyle{ \operatorname{Aut}(p) }[/math].

Now suppose [math]\displaystyle{ p:C \to X }[/math] is a covering map and [math]\displaystyle{ C }[/math] (and therefore also [math]\displaystyle{ X }[/math]) is connected and locally path connected. The action of [math]\displaystyle{ \operatorname{Aut}(p) }[/math] on each fiber is free. If this action is transitive on some fiber, then it is transitive on all fibers, and we call the cover regular (or normal or Galois). Every such regular cover is a principal [math]\displaystyle{ G }[/math]-bundle, where [math]\displaystyle{ G = \operatorname{Aut}(p) }[/math] is considered as a discrete topological group.

Every universal cover [math]\displaystyle{ p:D \to X }[/math] is regular, with deck transformation group being isomorphic to the fundamental group [math]\displaystyle{ \pi_1(X) }[/math].

Examples

• Let [math]\displaystyle{ q : S^1 \to S^1 }[/math] be the covering [math]\displaystyle{ q(z)=z^{n} }[/math] for some [math]\displaystyle{ n \in \mathbb{N} }[/math], then the map [math]\displaystyle{ d_k:S^1 \rightarrow S^1 : z \mapsto z \, e^{2\pi ik/n} }[/math] is a deck transformation and [math]\displaystyle{ \operatorname{Deck}(q)\cong \mathbb{Z}/ \mathbb{nZ} }[/math].
• Let [math]\displaystyle{ r : \mathbb{R} \to S^1 }[/math] be the covering [math]\displaystyle{ r(t)=(\cos(2 \pi t), \sin(2 \pi t)) }[/math], then the map [math]\displaystyle{ d_k:\mathbb{R} \rightarrow \mathbb{R} : t \mapsto t + k }[/math] with [math]\displaystyle{ k \in \mathbb{Z} }[/math] is a deck transformation and [math]\displaystyle{ \operatorname{Deck}(r)\cong \mathbb{Z} }[/math].
• As another important example, consider [math]\displaystyle{ \Complex }[/math] the complex plane and [math]\displaystyle{ \Complex^{\times} }[/math] the complex plane minus the origin. Then the map [math]\displaystyle{ p: \Complex^{\times} \to \Complex^{\times} }[/math] with [math]\displaystyle{ p(z) = z^{n} }[/math] is a regular cover. The deck transformations are multiplications with [math]\displaystyle{ n }[/math]-th roots of unity and the deck transformation group is therefore isomorphic to the cyclic group [math]\displaystyle{ \Z/n\Z }[/math]. Likewise, the map [math]\displaystyle{ \exp : \Complex \to \Complex^{\times} }[/math] with [math]\displaystyle{ \exp(z) = e^{z} }[/math] is the universal cover.

Properties

Let [math]\displaystyle{ X }[/math] be a path-connected space and [math]\displaystyle{ p:E \rightarrow X }[/math] be a connected covering. Since a deck transformation [math]\displaystyle{ d:E \rightarrow E }[/math] is bijective, it permutes the elements of a fiber [math]\displaystyle{ p^{-1}(x) }[/math] with [math]\displaystyle{ x \in X }[/math] and is uniquely determined by where it sends a single point. In particular, only the identity map fixes a point in the fiber.^[2]:70 Because of this property every deck transformation defines a group action on [math]\displaystyle{ E }[/math], i.e. let [math]\displaystyle{ U \subset X }[/math] be an open neighborhood of a [math]\displaystyle{ x \in X }[/math] and [math]\displaystyle{ \tilde U \subset E }[/math] an open neighborhood of an [math]\displaystyle{ e \in p^{-1}(x) }[/math], then [math]\displaystyle{ \operatorname{Deck}(p) \times E \rightarrow E: (d,\tilde U)\mapsto d(\tilde U) }[/math] is a group action.

Normal coverings

Definition

A covering [math]\displaystyle{ p:E \rightarrow X }[/math] is called normal, if [math]\displaystyle{ \operatorname{Deck}(p) \backslash E \cong X }[/math]. This means, that for every [math]\displaystyle{ x \in X }[/math] and any two [math]\displaystyle{ e_0,e_1 \in p^{-1}(x) }[/math] there exists a deck transformation [math]\displaystyle{ d:E \rightarrow E }[/math], such that [math]\displaystyle{ d(e_0)=e_1 }[/math].

Properties

Let [math]\displaystyle{ X }[/math] be a path-connected space and [math]\displaystyle{ p:E \rightarrow X }[/math] be a connected covering. Let [math]\displaystyle{ H=p_{\#}(\pi_1(E)) }[/math] be a subgroup of [math]\displaystyle{ \pi_1(X) }[/math], then [math]\displaystyle{ p }[/math] is a normal covering iff [math]\displaystyle{ H }[/math] is a normal subgroup of [math]\displaystyle{ \pi_1(X) }[/math].

If [math]\displaystyle{ p:E \rightarrow X }[/math] is a normal covering and [math]\displaystyle{ H=p_{\#}(\pi_1(E)) }[/math], then [math]\displaystyle{ \operatorname{Deck}(p) \cong \pi_1(X)/H }[/math].

If [math]\displaystyle{ p:E \rightarrow X }[/math] is a path-connected covering and [math]\displaystyle{ H=p_{\#}(\pi_1(E)) }[/math], then [math]\displaystyle{ \operatorname{Deck}(p) \cong N(H)/H }[/math], whereby [math]\displaystyle{ N(H) }[/math] is the normaliser of [math]\displaystyle{ H }[/math].^[2]:71

Let [math]\displaystyle{ E }[/math] be a topological space. A group [math]\displaystyle{ \Gamma }[/math] acts discontinuously on [math]\displaystyle{ E }[/math], if every [math]\displaystyle{ e \in E }[/math] has an open neighborhood [math]\displaystyle{ V \subset E }[/math] with [math]\displaystyle{ V \neq \empty }[/math], such that for every [math]\displaystyle{ \gamma \in \Gamma }[/math] with [math]\displaystyle{ \gamma V \cap V \neq \empty }[/math] one has [math]\displaystyle{ d_1 = d_2 }[/math].

If a group [math]\displaystyle{ \Gamma }[/math] acts discontinuously on a topological space [math]\displaystyle{ E }[/math], then the quotient map [math]\displaystyle{ q: E \rightarrow \Gamma \backslash E }[/math] with [math]\displaystyle{ q(e)=\Gamma e }[/math] is a normal covering.^[2]:72 Hereby [math]\displaystyle{ \Gamma \backslash E = \{\Gamma e: e \in E\} }[/math] is the quotient space and [math]\displaystyle{ \Gamma e = \{\gamma(e):\gamma \in \Gamma\} }[/math] is the orbit of the group action.

Examples

• The covering [math]\displaystyle{ q : S^1 \to S^1 }[/math] with [math]\displaystyle{ q(z)=z^{n} }[/math] is a normal coverings for every [math]\displaystyle{ n \in \mathbb{N} }[/math].
• Every simply connected covering is a normal covering.

Calculation

Let [math]\displaystyle{ \Gamma }[/math] be a group, which acts discontinuously on a topological space [math]\displaystyle{ E }[/math] and let [math]\displaystyle{ q: E \rightarrow \Gamma \backslash E }[/math] be the normal covering.

• If [math]\displaystyle{ E }[/math] is path-connected, then [math]\displaystyle{ \operatorname{Deck}(q) \cong \Gamma }[/math].^[2]:72

• If [math]\displaystyle{ E }[/math] is simply connected, then [math]\displaystyle{ \operatorname{Deck}(q)\cong \pi_1(\Gamma \backslash E) }[/math].^[2]:71

Examples

• Let [math]\displaystyle{ n \in \mathbb{N} }[/math]. The antipodal map [math]\displaystyle{ g:S^n \rightarrow S^n }[/math] with [math]\displaystyle{ g(x)=-x }[/math] generates, together with the composition of maps, a group [math]\displaystyle{ D(g) \cong \mathbb{Z/2Z} }[/math] and induces a group action [math]\displaystyle{ D(g) \times S^n \rightarrow S^n, (g,x)\mapsto g(x) }[/math], which acts discontinuously on [math]\displaystyle{ S^n }[/math]. Because of [math]\displaystyle{ \mathbb{Z_2} \backslash S^n \cong \mathbb{R}P^n }[/math] it follows, that the quotient map [math]\displaystyle{ q : S^n \rightarrow \mathbb{Z_2}\backslash S^n \cong \mathbb{R}P^n }[/math] is a normal covering and for [math]\displaystyle{ n \gt 1 }[/math] a universal covering, hence [math]\displaystyle{ \operatorname{Deck}(q)\cong \mathbb{Z/2Z}\cong \pi_1({\mathbb{R}P^n}) }[/math] for [math]\displaystyle{ n \gt 1 }[/math].
• Let [math]\displaystyle{ \mathrm{SO}(3) }[/math] be the special orthogonal group, then the map [math]\displaystyle{ f : \mathrm{SU}(2) \rightarrow \mathrm{SO}(3) \cong \mathbb{Z_2} \backslash \mathrm{SU}(2) }[/math] is a normal covering and because of [math]\displaystyle{ \mathrm{SU}(2) \cong S^3 }[/math], it is the universal covering, hence [math]\displaystyle{ \operatorname{Deck}(f) \cong \mathbb{Z/2Z} \cong \pi_1(\mathrm{SO}(3)) }[/math].
• With the group action [math]\displaystyle{ (z_1,z_2)*(x,y)=(z_1+(-1)^{z_2}x,z_2+y) }[/math] of [math]\displaystyle{ \mathbb{Z^2} }[/math] on [math]\displaystyle{ \mathbb{R^2} }[/math], whereby [math]\displaystyle{ (\mathbb{Z^2},*) }[/math] is the semidirect product [math]\displaystyle{ \mathbb{Z} \rtimes \mathbb{Z} }[/math], one gets the universal covering [math]\displaystyle{ f: \mathbb{R^2} \rightarrow (\mathbb{Z} \rtimes \mathbb{Z}) \backslash \mathbb{R^2} \cong K }[/math] of the klein bottle [math]\displaystyle{ K }[/math], hence [math]\displaystyle{ \operatorname{Deck}(f) \cong \mathbb{Z} \rtimes \mathbb{Z} \cong \pi_1(K) }[/math].
• Let [math]\displaystyle{ T = S^1 \times S^1 }[/math] be the torus which is embedded in the [math]\displaystyle{ \mathbb{C^2} }[/math]. Then one gets a homeomorphism [math]\displaystyle{ \alpha: T \rightarrow T: (e^{ix},e^{iy}) \mapsto (e^{i(x+\pi)},e^{-iy}) }[/math], which induces a discontinuous group action [math]\displaystyle{ G_{\alpha} \times T \rightarrow T }[/math], whereby [math]\displaystyle{ G_{\alpha} \cong \mathbb{Z/2Z} }[/math]. It follows, that the map [math]\displaystyle{ f: T \rightarrow G_{\alpha} \backslash T \cong K }[/math] is a normal covering of the klein bottle, hence [math]\displaystyle{ \operatorname{Deck}(f) \cong \mathbb{Z/2Z} }[/math].
• Let [math]\displaystyle{ S^3 }[/math] be embedded in the [math]\displaystyle{ \mathbb{C^2} }[/math]. Since the group action [math]\displaystyle{ S^3 \times \mathbb{Z/pZ} \rightarrow S^3: ((z_1,z_2),[k]) \mapsto (e^{2 \pi i k/p}z_1,e^{2 \pi i k q/p}z_2) }[/math] is discontinuously, whereby [math]\displaystyle{ p,q \in \mathbb{N} }[/math] are coprime, the map [math]\displaystyle{ f:S^3 \rightarrow \mathbb{Z_p} \backslash S^3 =: L_{p,q} }[/math] is the universal covering of the lens space [math]\displaystyle{ L_{p,q} }[/math], hence [math]\displaystyle{ \operatorname{Deck}(f) \cong \mathbb{Z/pZ} \cong \pi_1(L_{p,q}) }[/math].

Galois correspondence

Let [math]\displaystyle{ X }[/math] be a connected and locally simply connected space, then for every subgroup [math]\displaystyle{ H\subseteq \pi_1(X) }[/math] there exists a path-connected covering [math]\displaystyle{ \alpha:X_H \rightarrow X }[/math] with [math]\displaystyle{ \alpha_{\#}(\pi_1(X_H))=H }[/math].^[2]:66

Let [math]\displaystyle{ p_1:E \rightarrow X }[/math] and [math]\displaystyle{ p_2: E' \rightarrow X }[/math] be two path-connected coverings, then they are equivalent iff the subgroups [math]\displaystyle{ H = p_{1\#}(\pi_1(E)) }[/math] and [math]\displaystyle{ H'=p_{2\#}(\pi_1(E')) }[/math] are conjugate to each other.^[5]:482

Let [math]\displaystyle{ X }[/math] be a connected and locally simply connected space, then, up to equivalence between coverings, there is a bijection:

[math]\displaystyle{ \begin{matrix} \qquad \displaystyle \{\text{Subgroup of }\pi_1(X)\} & \longleftrightarrow & \displaystyle \{\text{path-connected covering } p:E \rightarrow X\} \\ H & \longrightarrow & \alpha:X_H \rightarrow X \\ p_\#(\pi_1(E))&\longleftarrow & p \\ \displaystyle \{\text{normal subgroup of }\pi_1(X)\} & \longleftrightarrow & \displaystyle \{\text{normal covering } p:E \rightarrow X\} \\ H & \longrightarrow & \alpha:X_H \rightarrow X \\ p_\#(\pi_1(E))&\longleftarrow & p \end{matrix} }[/math]

For a sequence of subgroups [math]\displaystyle{ \displaystyle \{\text{e}\} \subset H \subset G \subset \pi_1(X) }[/math] one gets a sequence of coverings [math]\displaystyle{ \tilde X \longrightarrow X_H \cong H \backslash \tilde X \longrightarrow X_G \cong G \backslash \tilde X \longrightarrow X\cong \pi_1(X) \backslash \tilde X }[/math]. For a subgroup [math]\displaystyle{ H \subset \pi_1(X) }[/math] with index [math]\displaystyle{ \displaystyle[\pi_1(X):H] = d }[/math], the covering [math]\displaystyle{ \alpha:X_H \rightarrow X }[/math] has degree [math]\displaystyle{ d }[/math].

Classification

Definitions

Category of coverings

Let [math]\displaystyle{ X }[/math] be a topological space. The objects of the category [math]\displaystyle{ \boldsymbol{Cov(X)} }[/math] are the coverings [math]\displaystyle{ p:E \rightarrow X }[/math] of [math]\displaystyle{ X }[/math] and the morphisms between two coverings [math]\displaystyle{ p:E \rightarrow X }[/math] and [math]\displaystyle{ q:F\rightarrow X }[/math] are continuous maps [math]\displaystyle{ f:E \rightarrow F }[/math], such that the diagram

commutes.

G-Set

Let [math]\displaystyle{ G }[/math] be a topological group. The category [math]\displaystyle{ \boldsymbol{G-Set} }[/math] is the category of sets which are G-sets. The morphisms are G-maps [math]\displaystyle{ \phi:X \rightarrow Y }[/math] between G-sets. They satisfy the condition [math]\displaystyle{ \phi(gx)=g \, \phi(x) }[/math] for every [math]\displaystyle{ g \in G }[/math].

Equivalence

Let [math]\displaystyle{ X }[/math] be a connected and locally simply connected space, [math]\displaystyle{ x \in X }[/math] and [math]\displaystyle{ G = \pi_1(X,x) }[/math] be the fundamental group of [math]\displaystyle{ X }[/math]. Since [math]\displaystyle{ G }[/math] defines, by lifting of paths and evaluating at the endpoint of the lift, a group action on the fiber of a covering, the functor [math]\displaystyle{ F:\boldsymbol{Cov(X)} \longrightarrow \boldsymbol{G-Set}: p \mapsto p^{-1}(x) }[/math] is an equivalence of categories.^[2]:68-70

Applications

Gimbal lock occurs because any map T³ → RP³ is not a covering map. In particular, the relevant map carries any element of T³, that is, an ordered triple (a,b,c) of angles (real numbers mod 2π), to the composition of the three coordinate axis rotations R_x(a)∘R_y(b)∘R_z(c) by those angles, respectively. Each of these rotations, and their composition, is an element of the rotation group SO(3), which is topologically RP³. This animation shows a set of three gimbals mounted together to allow three degrees of freedom. When all three gimbals are lined up (in the same plane), the system can only move in two dimensions from this configuration, not three, and is in gimbal lock. In this case it can pitch or yaw, but not roll (rotate in the plane that the axes all lie in).

An important practical application of covering spaces occurs in charts on SO(3), the rotation group. This group occurs widely in engineering, due to 3-dimensional rotations being heavily used in navigation, nautical engineering, and aerospace engineering, among many other uses. Topologically, SO(3) is the real projective space RP³, with fundamental group Z/2, and only (non-trivial) covering space the hypersphere S³, which is the group Spin(3), and represented by the unit quaternions. Thus quaternions are a preferred method for representing spatial rotations – see quaternions and spatial rotation.

However, it is often desirable to represent rotations by a set of three numbers, known as Euler angles (in numerous variants), both because this is conceptually simpler for someone familiar with planar rotation, and because one can build a combination of three gimbals to produce rotations in three dimensions. Topologically this corresponds to a map from the 3-torus T³ of three angles to the real projective space RP³ of rotations, and the resulting map has imperfections due to this map being unable to be a covering map. Specifically, the failure of the map to be a local homeomorphism at certain points is referred to as gimbal lock, and is demonstrated in the animation at the right – at some points (when the axes are coplanar) the rank of the map is 2, rather than 3, meaning that only 2 dimensions of rotations can be realized from that point by changing the angles. This causes problems in applications, and is formalized by the notion of a covering space.

See also

• Bethe lattice is the universal cover of a Cayley graph
• Covering graph, a covering space for an undirected graph, and its special case the bipartite double cover
• Covering group
• Galois connection
• Quotient space (topology)

Literature

• Hatcher, Allen (2002). Algebraic topology. Cambridge: Cambridge University Press. ISBN 0-521-79160-X. OCLC 45420394. 
• Forster, Otto (1981). Lectures on Riemann surfaces. New York. ISBN 0-387-90617-7. OCLC 7596520. 
• Munkres, James R. (2018). Topology. New York, NY. ISBN 978-0-13-468951-7. OCLC 964502066. 
• Kühnel, Wolfgang (2011) (in de). Matrizen und Lie-Gruppen Eine geometrische Einführung. Wiesbaden: Vieweg+Teubner Verlag. doi:10.1007/978-3-8348-9905-7. ISBN 978-3-8348-9905-7. OCLC 706962685. 

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Covering space. Read more