Coxeter element

In mathematics, a Coxeter element is an element of an irreducible Coxeter group which is a product of all simple reflections. The product depends on the order in which they are taken, but different orderings produce conjugate elements, which have the same order. This order is known as the Coxeter number. They are named after British-Canadian geometer H.S.M. Coxeter, who introduced the groups in 1934 as abstractions of reflection groups.^[1]

Definitions

Note that this article assumes a finite Coxeter group. For infinite Coxeter groups, there are multiple conjugacy classes of Coxeter elements, and they have infinite order.

There are many different ways to define the Coxeter number h of an irreducible root system.

• The Coxeter number is the order of any Coxeter element;.
• The Coxeter number is [math]\displaystyle{ \tfrac{2m}{n}, }[/math] where n is the rank, and m is the number of reflections. In the crystallographic case, m is half the number of roots; and 2m+n is the dimension of the corresponding semisimple Lie algebra.
• If the highest root is [math]\displaystyle{ \sum m_i \alpha_i }[/math] for simple roots α_i, then the Coxeter number is [math]\displaystyle{ 1 + \sum m_i. }[/math]
• The Coxeter number is the highest degree of a fundamental invariant of the Coxeter group acting on polynomials.

The Coxeter number for each Dynkin type is given in the following table:

Coxeter group		Coxeter diagram	Dynkin diagram	Reflections [math]\displaystyle{ m=\tfrac{nh}{2} }[/math][2]	Coxeter number h	Dual Coxeter number	Degrees of fundamental invariants
An	[3,3...,3]	...	Script error: No such module "Dynkin"....Script error: No such module "Dynkin".	[math]\displaystyle{ \frac{n(n+1)}{2} }[/math]	n + 1	n + 1	2, 3, 4, ..., n + 1
Bn	[4,3...,3]	...	Script error: No such module "Dynkin"....Script error: No such module "Dynkin".	n2	2n	2n − 1	2, 4, 6, ..., 2n
Cn			Script error: No such module "Dynkin"....Script error: No such module "Dynkin".			n + 1
Dn	[3,3,...31,1]	...	Script error: No such module "Dynkin"....Script error: No such module "Dynkin".	n(n − 1)	2n − 2	2n − 2	n; 2, 4, 6, ..., 2n − 2
E6	[32,2,1]		36	12	12	2, 5, 6, 8, 9, 12
E7	[33,2,1]		63	18	18	2, 6, 8, 10, 12, 14, 18
E8	[34,2,1]		120	30	30	2, 8, 12, 14, 18, 20, 24, 30
F4	[3,4,3]		Script error: No such module "Dynkin". Script error: No such module "Dynkin".	24	12	9	2, 6, 8, 12
G2	[6]		Script error: No such module "Dynkin". Script error: No such module "Dynkin".	6	6	4	2, 6
H3	[5,3]		-	15	10		2, 6, 10
H4	[5,3,3]		-	60	30		2, 12, 20, 30
I2(p)	[p]		-	p	p		2, p

The invariants of the Coxeter group acting on polynomials form a polynomial algebra whose generators are the fundamental invariants; their degrees are given in the table above. Notice that if m is a degree of a fundamental invariant then so is h + 2 − m.

The eigenvalues of a Coxeter element are the numbers [math]\displaystyle{ e^{2\pi i\frac{m-1}{h}} }[/math] as m runs through the degrees of the fundamental invariants. Since this starts with m = 2, these include the primitive hth root of unity, [math]\displaystyle{ \zeta_h = e^{2\pi i\frac{1}{h}}, }[/math] which is important in the Coxeter plane, below.

The dual Coxeter number is 1 plus the sum of the coefficients of simple roots in the highest short root of the dual root system.

Group order

There are relations between the order g of the Coxeter group and the Coxeter number h:^[3] [math]\displaystyle{ \begin{align} {} [p]:& \quad \frac{2h}{g_p} = 1 \\[4pt] [p,q]:& \quad \frac{8}{g_{p,q}} = \frac{2}{p} + \frac{2}{q} -1 \\[4pt] [p,q,r]:& \quad \frac{64h}{g_{p,q,r}} = 12 - p - 2q - r + \frac{4}{p} + \frac{4}{r} \\[4pt] [p,q,r,s]:& \quad \frac{16}{g_{p,q,r,s}} = \frac{8}{g_{p,q,r}} + \frac{8}{g_{q,r,s}} + \frac{2}{ps} - \frac{1}{p} - \frac{1}{q} - \frac{1}{r} - \frac{1}{s} +1 \\[4pt] \vdots \qquad & \qquad \vdots \end{align} }[/math]

For example, [3,3,5] has h = 30: [math]\displaystyle{ \begin{align} &\frac{64 \times 30}{g_{3,3,5}} = 12 - 3 - 6 - 5 + \frac{4}{3} + \frac{4}{5} = \frac{2}{15}, \\[4pt] &\therefore g_{3,3,5} = \frac{1920\times 15}{2} = 960 \times 15 = 14400. \end{align} }[/math]

Coxeter elements

Distinct Coxeter elements correspond to orientations of the Coxeter diagram (i.e. to Dynkin quivers): the simple reflections corresponding to source vertices are written first, downstream vertices later, and sinks last. (The choice of order among non-adjacent vertices is irrelevant, since they correspond to commuting reflections.) A special choice is the alternating orientation, in which the simple reflections are partitioned into two sets of non-adjacent vertices, and all edges are oriented from the first to the second set.^[4] The alternating orientation produces a special Coxeter element w satisfying [math]\displaystyle{ w^{h/2}= w_0, }[/math] where w₀ is the longest element, provided the Coxeter number h is even.

For [math]\displaystyle{ A_{n-1} \cong S_n, }[/math] the symmetric group on n elements, Coxeter elements are certain n-cycles: the product of simple reflections [math]\displaystyle{ (1,2) (2,3) \cdots (n-1,n) }[/math] is the Coxeter element [math]\displaystyle{ (1,2,3,\dots, n) }[/math].^[5] For n even, the alternating orientation Coxeter element is: [math]\displaystyle{ (1,2)(3,4)\cdots (2,3)(4,5) \cdots = (2,4,6,\ldots,n{-}2,n, n{-}1,n{-}3,\ldots,5,3,1). }[/math] There are [math]\displaystyle{ 2^{n-2} }[/math] distinct Coxeter elements among the [math]\displaystyle{ (n{-}1)! }[/math] n-cycles.

The dihedral group Dih_p is generated by two reflections that form an angle of [math]\displaystyle{ \tfrac{2\pi}{2p}, }[/math] and thus the two Coxeter elements are their product in either order, which is a rotation by [math]\displaystyle{ \pm \tfrac{2\pi}{p}. }[/math]

Coxeter plane

Projection of E₈ root system onto Coxeter plane, showing 30-fold symmetry.

For a given Coxeter element w, there is a unique plane P on which w acts by rotation by [math]\displaystyle{ \tfrac{2\pi}{h}. }[/math] This is called the Coxeter plane^[6] and is the plane on which P has eigenvalues [math]\displaystyle{ e^{2\pi i\frac{1}{h}} }[/math] and [math]\displaystyle{ e^{-2\pi i\frac{1}{h}} = e^{2\pi i\frac{h-1}{h}}. }[/math]^[7] This plane was first systematically studied in (Coxeter 1948),^[8] and subsequently used in (Steinberg 1959) to provide uniform proofs about properties of Coxeter elements.^[8]

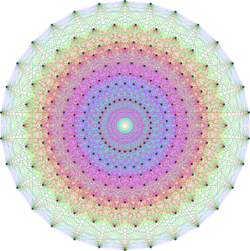
The Coxeter plane is often used to draw diagrams of higher-dimensional polytopes and root systems – the vertices and edges of the polytope, or roots (and some edges connecting these) are orthogonally projected onto the Coxeter plane, yielding a Petrie polygon with h-fold rotational symmetry.^[9] For root systems, no root maps to zero, corresponding to the Coxeter element not fixing any root or rather axis (not having eigenvalue 1 or −1), so the projections of orbits under w form h-fold circular arrangements^[9] and there is an empty center, as in the E₈ diagram at above right. For polytopes, a vertex may map to zero, as depicted below. Projections onto the Coxeter plane are depicted below for the Platonic solids.

In three dimensions, the symmetry of a regular polyhedron, {p, q}, with one directed Petrie polygon marked, defined as a composite of 3 reflections, has rotoinversion symmetry S_h, [2⁺,h⁺], order h. Adding a mirror, the symmetry can be doubled to antiprismatic symmetry, D_hd, [2⁺,h], order 2h. In orthogonal 2D projection, this becomes dihedral symmetry, Dih_h, [h], order 2h.

Coxeter group	A3 Td	B3 Oh		H3 Ih
Regular polyhedron	Tetrahedron {3,3}	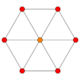Cube {4,3}	Octahedron {3,4}	Dodecahedron {5,3}	Icosahedron {3,5}
Symmetry	S4, [2+,4+], (2×) D2d, [2+,4], (2*2)	S6, [2+,6+], (3×) D3d, [2+,6], (2*3)		S10, [2+,10+], (5×) D5d, [2+,10], (2*5)
Coxeter plane symmetry	Dih4, [4], (*4•)	Dih6, [6], (*6•)		Dih10, [10], (*10•)
Petrie polygons of the Platonic solids, showing 4-fold, 6-fold, and 10-fold symmetry.

In four dimensions, the symmetry of a regular polychoron, {p, q, r}, with one directed Petrie polygon marked is a double rotation, defined as a composite of 4 reflections, with symmetry +¹/_h[C_h×C_h]^[10] (John H. Conway), (C_2h/C₁;C_2h/C₁) (#1', Patrick du Val (1964)^[11]), order h.

Coxeter group	A4	B4		F4	H4
Regular polychoron	5-cell {3,3,3}	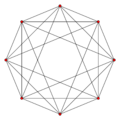16-cell {3,3,4}	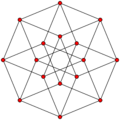Tesseract {4,3,3}	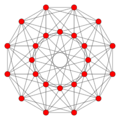24-cell {3,4,3}	120-cell {5,3,3}	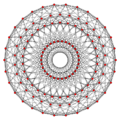600-cell {3,3,5}
Symmetry	+1/5[C5×C5]	+1/8[C8×C8]		+1/12[C12×C12]	+1/30[C30×C30]
Coxeter plane symmetry	Dih5, [5], (*5•)	Dih8, [8], (*8•)		Dih12, [12], (*12•)	Dih30, [30], (*30•)
Petrie polygons of the regular 4D solids, showing 5-fold, 8-fold, 12-fold and 30-fold symmetry.

In five dimensions, the symmetry of a regular 5-polytope, {p, q, r, s}, with one directed Petrie polygon marked, is represented by the composite of 5 reflections.

Coxeter group	A5	B5		D5
Regular polyteron	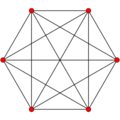5-simplex {3,3,3,3}	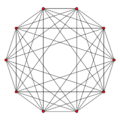5-orthoplex {3,3,3,4}	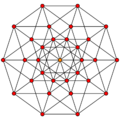5-cube {4,3,3,3}	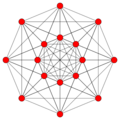5-demicube h{4,3,3,3}
Coxeter plane symmetry	Dih6, [6], (*6•)	Dih10, [10], (*10•)		Dih8, [8], (*8•)

In dimensions 6 to 8 there are 3 exceptional Coxeter groups; one uniform polytope from each dimension represents the roots of the exceptional Lie groups E_n. The Coxeter elements are 12, 18 and 30 respectively.

E_n groups

Coxeter group	E6	E7	E8
Graph	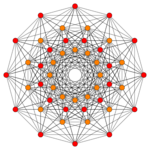122	231	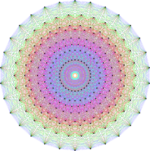421
Coxeter plane symmetry	Dih12, [12], (*12•)	Dih18, [18], (*18•)	Dih30, [30], (*30•)

See also

• Longest element of a Coxeter group

Notes

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Coxeter element. Read more