DEVS
 From HandWiki - Reading time: 37 min
From HandWiki - Reading time: 37 min
DEVS, abbreviating discrete event system specification, is a modular and hierarchical formalism for modeling and analyzing general systems that can be discrete event systems which might be described by state transition tables, and continuous state systems which might be described by differential equations, and hybrid continuous state and discrete event systems. DEVS is a timed event system.
History
DEVS is a formalism for modeling and analysis of discrete event systems (DESs). The DEVS formalism was invented by Bernard P. Zeigler, who is emeritus professor at the University of Arizona. DEVS was introduced to the public in Zeigler's first book, Theory of Modeling and Simulation in 1976,[1] while Zeigler was an associate professor at University of Michigan. DEVS can be seen as an extension of the Moore machine formalism,[2] which is a finite state automaton where the outputs are determined by the current state alone (and do not depend directly on the input). The extension was done by
- associating a lifespan with each state,[1]
- providing a hierarchical concept with an operation, called coupling,[3]
Since the lifespan of each state is a real number (more precisely, non-negative real) or infinity, it is distinguished from discrete time systems, sequential machines, and Moore machines, in which time is determined by a tick time multiplied by non-negative integers. Moreover, the lifespan can be a random variable; for example the lifespan of a given state can be distributed exponentially or uniformly. The state transition and output functions of DEVS can also be stochastic.
Zeigler proposed a hierarchical algorithm for DEVS model simulation in 1984[4] which was published in Simulation journal in 1987. Since then, many extended formalism from DEVS have been introduced with their own purposes: DESS/DEVS for combined continuous and discrete event systems, P-DEVS for parallel DESs, G-DEVS for piecewise continuous state trajectory modeling of DESs, RT-DEVS for realtime DESs, cell-DEVS for cellular DESs, fuzzy-DEVS for fuzzy DESs, dynamic structuring DEVS for DESs changing their coupling structures dynamically, and so on. In addition to its extensions, there are some subclasses such as SP-DEVS and FD-DEVS have been researched for achieving decidability of system properties.
Due to the modular and hierarchical modeling views, as well as its simulation-based analysis capability, the DEVS formalism and its variations have been used in many application of engineering (such as hardware design, hardware/software codesign, communications systems, manufacturing systems) and science (such as biology, and sociology)
Formalism

Intuitive example
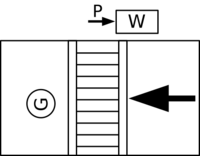
DEVS defines system behavior as well as system structure. System behavior in DEVS formalism is described using input and output events as well as states. For example, for the ping-pong player of Fig. 1, the input event is ?receive, and the output event is !send. Each player, A, B, has its states: Send and Wait. Send state takes 0.1 seconds to send back the ball that is the output event !send, while the Wait state lasts until the player receives the ball that is the input event ?receive.
The structure of ping-pong game is to connect two players: player A's output event !send is transmitted to player B's input event ?receive, and vice versa.
In the classic DEVS formalism, atomic DEVS captures the system behavior, while coupled DEVS describes the structure of system.
The following formal definition is for classic DEVS.[5] In this article, we will use the time base, that is the set of non-negative real numbers; the extended time base, that is the set of non-negative real numbers plus infinity.
Atomic DEVS
An atomic DEVS model is defined as a 7-tuple
where
- is the set of input events;
- is the set of output events;
- is the set of sequential states (or also called the set of partial states);
- is the initial state;
- is the time advance function which is used to determine the lifespan of a state;
- is the external transition function which defines how an input event changes a state of the system, where is the set of total states, and is the elapsed time since the last event;[6]
- is the internal transition function which defines how a state of the system changes internally (when the elapsed time reaches to the lifetime of the state);
- is the output function where and is a silent event or an unobserved event. This function defines how a state of the system generates an output event (when the elapsed time reaches to the lifetime of the state);
- The atomic DEVS model for ping-pong players
The atomic DEVS model for player A of Fig. 1 is given player=
such that
Both player A and player B are atomic DEVS models.
Simply speaking, there are two cases that an atomic DEVS model can change its state : (1) when an external input comes into the system ; (2) when the elapsed time reaches the lifespan of which is defined by . At the same time of (2), generates an output which is defined by .
For formal behavior description of given an atomic DEVS model, refer to the section about behavior of atomic DEVS. Computer algorithms to implement the behavior of a given atomic DEVS model are available in the section about simulation algorithms for atomic DEVS.
Coupled DEVS
The coupled DEVS defines which sub-components belong to it and how they are connected with each other. A coupled DEVS model is defined as an 8-tuple
where
- is the set of input events;
- is the set of output events;
- is the name set of sub-components;
- is the set of sub-components where for each can be either an atomic DEVS model or a coupled DEVS model.
- is the set of external input couplings;
- is the set of internal couplings;
- is the external output coupling function;
- is the tie-breaking function which defines how to select the event from the set of simultaneous events;
- The coupled DEVS model for ping-pong game
The ping-pong game of Fig. 1 can be modeled as a coupled DEVS model where ;;; is described as above; ; ; and .
Simply speaking, like the behavior of the atomic DEVS class, a coupled DEVS model changes its components' states (1) when an external event comes into ; (2) when one of components where executes its internal state transition and generates its output . In both cases (1) and (2), a triggering event is transmitted to all influences which are defined by coupling sets and .
For formal definition of behavior of the coupled DEVS, you can refer to the section about behavior of coupled DEVS. Computer algorithms to implement the behavior of a given coupled DEVS mode are available at the section about simulation algorithms for coupled DEVS.
Analysis methods
Simulation for discrete event systems
The simulation algorithm of DEVS models considers two issues: time synchronization and message propagation. Time synchronization of DEVS is to control all models to have the identical current time. However, for an efficient execution, the algorithm makes the current time jump to the most urgent time when an event is scheduled to execute its internal state transition as well as its output generation. Message propagation is to transmit a triggering message which can be either an input or output event along the associated couplings which are defined in a coupled DEVS model. For more detailed information, the reader can refer to simulation algorithms for atomic DEVS and simulation algorithms for coupled DEVS.
Simulation for continuous state systems
By introducing a quantization method which abstracts a continuous segment as a piecewise const segment, DEVS can simulate behaviors of continuous state systems which are described by networks of differential algebraic equations. This research has been initiated by Zeigler in 1990s.[7] Many properties have been clarified by Prof. Kofman in 2000s and Dr. Nutaro. In 2006, Prof. Cellier who is the author of Continuous System Modeling,[8] and Prof. Kofman wrote a text book, Continuous System Simulation,[9] in which chapters 11 and 12 cover how DEVS simulates continuous state systems. Dr. Nutaro's book,[10] covers the discrete event simulation of continuous state systems too.[11]
Verification for discrete event systems
As an alternative analysis method against the sampling-based simulation method, an exhaustive generating behavior approach, generally called verification has been applied for analysis of DEVS models. It is proven that infinite states of a given DEVS model (especially a coupled DEVS model ) can be abstracted by behaviorally isomorphic finite structure, called a reachability graph when the given DEVS model is a sub-class of DEVS such as schedule-preserving DEVS (SP-DEVS), finite & deterministic DEVS (FD-DEVS),[12] and finite & real-time DEVS (FRT-DEVS).[13] As a result, based on the reachability graph, (1) dead-lock and live-lock freeness as qualitative properties are decidable with SP-DEVS,[14] FD-DEVS,[15] and FRT-DEVS;[13] and (2) min/max processing time bounds as a quantitative property are decidable with SP-DEVS so far by 2012.
Timed event system
The general system has been described by Zeigler[16][17] with the standpoints to define (1) the time base, (2) the admissible input segments, (3) the system states, (4) the state trajectory with an admissible input segment, (5) the output for a given state. A timed event system defining the state trajectory associated with the current and event segments came from the class of general system to allows non-deterministic behaviors in it.[18] Since the behaviors of DEVS can be described by timed event system, DEVS and RTDEVS is a sub-class or an equivalent class of timed event system.
A timed event system is a structure
where
- is the set of events;
- is the set of states;
- is the set of initial states;
- is the set of accepting states;
- is the set of state trajectories in which indicates that a state can change into along with an event segment . If two state trajectories and are called contiguous if , and two event trajectories and are contiguous. Two contiguous state trajectories and implies .
Given a timed event system
, the set of its behaviors is called its language depending on the observation time length. Let
be the observation time length. If
,
-length observation language of
is denoted by
, and defined as
We call an event segment
a
-length behavior of
, if
. By sending the observation time length
to infinity, we define infinite length observation language of
is denoted by
, and defined as
We call an event segment
an infinite-length behavior of
, if
.
Variations of DEVS
Extensions (superclassing)
Numerous extensions of the classic DEVS formalism have been developed in the last decades. Among them formalisms which allow to have changing model structures while the simulation time evolves.
G-DEVS,[19][20] parallel DEVS, dynamic structuring DEVS, cell-DEVS,[21] dynDEVS, fuzzy-DEVS, GK-DEVS, ml-DEVS, symbolic DEVS, real-time DEVS, rho-DEVS
Restrictions (subclassing)
There are some sub-classes known as schedule-preserving DEVS (SP-DEVS) and finite and deterministic DEVS (FD-DEVS) which were designated to support verification analysis. SP-DEVS and FD-DEVS whose expressiveness are E(SP-DEVS) E(FD-DEVS) E(DEVS) where E(formalism) denotes the expressiveness of formalism.
Behavior
Atomic DEVS
The behavior of a given DEVS model is a set of sequences of timed events including null events, called event segments, which make the model move from one state to another within a set of legal states. To define it this way, the concept of a set of illegal state as well a set of legal states needs to be introduced.
In addition, since the behavior of a given DEVS model needs to define how the state transition change both when time is passed by and when an event occurs, it has been described by a much general formalism, called general system.[22] In this article, we use a sub-class of general system formalism, called timed event system instead.
Depending on how the total state and the external state transition function of a DEVS model are defined, there are two ways to define the behavior of a DEVS model using timed event system. Since the behavior of a coupled DEVS model is defined as an atomic DEVS model, the behavior of coupled DEVS class is also defined by timed event system.
View 1: total states = states * elapsed times
Suppose that a DEVS model, has
- the external state transition .
- the total state set where denotes elapsed time since last event and denotes the set of non-negative real numbers, and
Then the DEVS model,
is a timed event system
where
- The event set .
- The state set where .
- The set of initial states .
- The set of accepting states
- The set of state trajectories is defined for two different cases: and . For a non-accepting state , there is no change together with any even segment so
For a total state at time and an event segment as follows.
is the null event segment, i.e.
is a timed event
where the event is an input event
,
is a timed event
where the event is an output event or the unobservable event
,
Computer algorithms to simulate this view of behavior are available at simulation algorithms for atomic DEVS section.
View 2: total states = states * lifespans * elapsed times
Suppose that a DEVS model, has
- the total state set where denotes lifespan of state , denotes elapsed time since last update, and denotes the set of non-negative real numbers plus infinity,
- the external state transition is .
Then the DEVS
is a timed event system
where
- The event set .
- The state set where .
- The set of initial states.
- The set of acceptance states .
- The set of state trajectories is depending on two cases: and . For a non-accepting state , there is no changes together with any segment so
For a total state at time and an event segment as follows.
is the null event segment, i.e.
is a timed event
where the event is an input event
,
is a timed event
where the event is an output event or the unobservable event
,
Computer algorithms to simulate this view of behavior are available at simulation algorithms for atomic DEVS section.
Comparison of view1 and view2
Features of view1
View1 has been introduced by Zeigler[23] in which given a total state
and
where
is the remaining time.[23][22] In other words, the set of partial states is indeed
where
is a state set. When a DEVS model receives an input event
, view1 resets the elapsed time
by zero, if the DEVS model needs to ignore
in terms of the lifespan control, modelers have to update the remaining time
in the external state transition function
that is the responsibility of the modelers.
Since the number of possible values of is the same as the number of possible input events coming to the DEVS model, that is unlimited. As a result, the number of states is also unlimited that is the reason why view2 has been proposed.
If we don't care the finite-vertex reachability graph of a DEVS model, view1 has an advantage of simplicity for treating the elapsed time every time any input event arrives into the DEVS model. But disadvantage might be modelers of DEVS should know how to manage as above, which is not explicitly explained in itself but in .
Features of view2
View2 has been introduced by Hwang and Zeigler[24][25] in which given a total state
, the remaining time,
is computed as
When a DEVS model receives an input event
, view2 resets the elapsed time
by zero only if
. If the DEVS model needs to ignore
in terms of the lifespan control, modelers can use
.
Unlike view1, since the remaining time is not component of in nature, if the number of states, i.e. is finite, we can draw a finite-vertex (as well as edge) state-transition diagram.[24][25] As a result, we can abstract behavior of such a DEVS-class network, for example SP-DEVS and FD-DEVS, as a finite-vertex graph, called reachability graph.[24][25]
Coupled DEVS
DEVS is closed under coupling.[3][26] In other words, given a coupled DEVS model , its behavior is described as an atomic DEVS model . For a given coupled DEVS , once we have an equivalent atomic DEVS , behavior of can be referred to behavior of atomic DEVS which is based on timed event system.
Similar to behavior of atomic DEVS, behavior of the coupled DEVS class is described depending on definition of the total state set and its handling as follows.
View1: Total states = states * elapsed times
Given a coupled DEVS model , its behavior is described as an atomic DEVS model
where
- and are the input event set and the output event set, respectively.
- is the partial state set where is the total state set of component (Refer to view1 of behavior of DEVS), where is the set of non-negative real numbers.
- is the initial state set where is the total initial state of component .
- is the time advance function, where is the set of non-negative real numbers plus infinity. Given ,
- is the external state function. Given a total state where , and input event , the next state is given by
where
Given the partial state
, let
denote the set of imminent components. The firing component
which triggers the internal state transition and an output event is determined by
- is the internal state function. Given a partial state , the next state is given by
where
- is the output function. Given a partial state ,
View2: Total states = states * lifespan * elapsed times
Given a coupled DEVS model , its behavior is described as an atomic DEVS model
where
- and are the input event set and the output event set, respectively.
- is the partial state set where is the total state set of component (Refer to view2 of behavior of DEVS section).
- is the initial state set where is the total initial state of component .
- is the time advance function. Given ,
- is the external state function. Given a total state where , and input event , the next state is given by
where
and
Given the partial state
, let
denote the set of imminent components. The firing component
which triggers the internal state transition and an output event is determined by
- is the internal state function. Given a partial state , the next state is given by
where
- is the output function. Given a partial state ,
Time passage
Since in a coupled DEVS model with non-empty sub-components, i.e., , the number of clocks which trace their elapsed times are multiple, so time passage of the model is noticeable.
For view1
Given a total state where
If unit event segment
is the null event segment, i.e.
, the state trajectory in terms of timed event system is
For view2
Given a total state where
If unit event segment
is the null event segment, i.e.
, the state trajectory in terms of timed event system is
Simulation algorithms
Atomic DEVS
Given an atomic DEVS model, simulation algorithms are methods to generate the model's legal behaviors which are trajectories not to reach to illegal states. (see Behavior of DEVS). Zeigler originally introduced the algorithms that handle time variables related to lifespan
and elapsed time
by introducing two other time variables, last event time,
, and next event time
with the following relations:[3]
and
where
denotes the current time. And the remaining time,
is equivalently computed as
, apparently
.
Since the behavior of a given atomic DEVS model can be defined in two different views depending on the total state and the external transition function (refer to behavior of DEVS section), the simulation algorithms are also introduced in two different views as below.
Common parts
Regardless of two different views of total states, algorithms for initialization and internal transition cases are commonly defined as below.
DEVS-simulator variables: parent // parent coordinator // time of last event // time of next event // the associated Atomic DEVS model when receive init-message(Time ) when receive star-message(Time ) if then error: bad synchronization; send y-message() to parent;
View 1: total states = states * elapsed times
As addressed in behavior of atomic DEVS section, when DEVS receives an input event, right calling , the last event time, is set by the current time,, thus the elapsed time becomes zero because .
when receive x-message(, Time ) if and == false then error: bad synchronization;
View 2: total states = states * lifespans * elapsed times
Notice that as addressed in behavior of atomic DEVS section, depending on the value of return by , last event time,, and next event time,,consequently, elapsed time, , and lifespan, are updated (if ) or preserved (if ).
when receive x-message(, Time ) if and == false then error: bad synchronization; if then
Coupled DEVS
Given a coupled DEVS model, simulation algorithms are methods to generate the model's legal behaviors, which are a set of trajectories not to reach illegal states. (see behavior of a coupled DEVS model.) Zeigler originally introduced the algorithms that handle time variables related to lifespan
and elapsed time
by introducing two other time variables, last event time,
, and next event time
with the following relations:[3]
and
where
denotes the current time. And the remaining time,
is equivalently computed as
apparently
. Based on these relationships, the algorithms to simulate the behavior of a given coupled DEVS are written as follows.
algorithm DEVS-coordinator Variables: parent // parent coordinator : // time of last event : // time of next event // the associated coupled DEVS model when receive init-message(Time t) for each do send init-message(t) to child ; ; when receive star-message(Time t) if then error: bad synchronization; send star-message(t)to ; ; when receive x-message(, Time t) if and == false then error: bad synchronization; for each do send x-message(,t) to child ; ; when receive y-message(, Time t) for each do send x-message(,t) to child if then send y-message(, t) to parent; ; ;
FD-DEVS
FD-DEVS (finite & deterministic discrete event system specification) is a formalism for modeling and analyzing discrete event dynamic systems in both simulation and verification ways. FD-DEVS also provides modular and hierarchical modeling features which have been inherited from Classic DEVS.
History
FD-DEVS was originally named as schedule-controllable DEVS[27] and designed to support verification analysis of its networks which had been an open problem of DEVS formalism for 30 years. In addition, it was also designated to resolve the so-called "OPNA" problem of SP-DEVS. From the viewpoint of classic DEVS, FD-DEVS has three restrictions
- finiteness of event sets and state set,
- the lifespan of a state can be scheduled by a rational number or infinity, and
- the internal schedule can be either preserved or updated by an input event.
The third restriction can be also seen as a relaxation from SP-DEVS where the schedule is always preserved by any input events. Due to this relaxation there is no longer OPNA problem, but there is also one limitation that a time-line abstraction which can be used for abstracting elapsed times of SP-DEVS networks is no longer useful for FD-DEVS network.[27] But another time abstraction method[28] which was invented by Prof. D. Dill can be applicable to obtain a finite-vertex reachability graph for FD-DEVS networks.
Examples
Ping-pong game

Consider a single ping-pong match in which there are two players. Each player can be modeled by FD-DEVS such that the player model has an input event ?receive and an output event !send, and it has two states: Send and Wait. Once the player gets into "Send", it will generates "!send" and go back to "Wait" after the sending time which is 0.1 time unit. When staying at "Wait" and if it gets "?receive", it changes into "Send" again. In other words, the player model stays at "Wait" forever unless it gets "?receive".
To make a complete ping-pong match, one player starts as an offender whose initial state is "Send" and the other starts as a defender whose initial state is "Wait". Thus in Fig. 1. player A is the initial offender and player B is the initial defender. In addition, to make the game continue, each player's "?send" event should be coupled to the other player's "?receive" as shown in Fig. 1.
Two-slot toaster

Consider a toaster in which there are two slots that have their own start knobs as shown in Fig. 2(a). Each slot has the identical functionality except their toasting time. Initially, the knob is not pushed, but if one pushes the knob, the associated slot starts toasting for its toasting time: 20 seconds for the left slot, 40 seconds for the right slot. After the toasting time, each slot and its knobs pop up. Notice that even though one tries to push a knob when its associated slot is toasting, nothing happens.
One can model it with FD-DEVS as shown in Fig. 2(b). Two slots are modeled as atomic FD-DEVS whose input event is "?push" and output event is "!pop", states are "Idle" (I) and "Toast" (T) with the initial state is "idle". When it is "Idle" and receives "?push" (because one pushes the knob), its state changes to "Toast". In other words, it stays at "Idle" forever unless it receives "?push" event. 20 (res. 40) seconds later the left (res. right) slot returns to "Idle".
Atomic FD-DEVS
Formal definition
where
- is a finite set of input events;
- is a finite set of output events;
- is a finite set of states;
- is the initial state;
- is the time advance function which defines the lifespan of a state where is the set of non-negative rational numbers plus infinity.
- is the external transition function which defines how an input event changes the schedule as well as a state of the system. The internal schedule of a state is updated by if , otherwise(i.e., ), the schedule is preserved.[29]
- is the output and internal transition function where and denotes the silent event. The output and internal transition function defines how a state generates an output event, at the same time, how the state changes internally.[30]
- Formal representation of ping-pong player
The formal representation of the player in the ping-pong example shown in Fig. 1 can be given as follows. where ={?receive}; ={!send}; ={Send, Wait}; =Send for player A, Wait for player B; (Send)=0.1,(Wait)=; (Wait,?receive)=(Send,1), (Send,?receive)=(Send,0); (Send)=(!send, Wait), (Wait)=(, Wait).
- Formal representation of one slot toaster
The formal representation of the slot of Two-slot Toaster Fig. 2(a) and (b) can be given as follows. where ={?push}; ={!pop}; ={I, T}; =I; (T)=20 for the left slot, 40 for the right slot, (I)=; (I, ?push)=(T,1), (T,?push)=(T,0); (T)=(!pop, I), (I)=(, I).
- Formal representation of crosswalk light controller
As mentioned above, FD-DEVS is an relaxation of SP-DEVS. That means, FD-DEVS is a supper class of SP-DEVS. We would give a model of FD-DEVS of a crosswalk light controller which is used for SP-DEVS in this Wikipedia. where ={?p}; ={!g:0, !g:1, !w:0, !w:1}; ={BG, BW, G, GR, R, W, D}; =BG, (BG)=0.5,(BW)=0.5, (G)=30, (GR)=30,(R)=2, (W)=26, (D)=2; (G,?p)=(GR,0), (s,?p)=(s,0) if s G; (BG)=(!g:1, BW), (BW)=(!w:0, G),(G)=(, G), (GR)=(!g:0, R), (R)=(!w:1, W), (W)=(!w:0, D), (D)=(!g:1, G);
Behaviors of FD-DEVS models
- FD-DEVS is a sub-class of DEVS
A FD-DEVS model, is DEVS where
- of are the same as those of .
- Given a state ,
- Given a state and an input event ,
- Given a state , if
- Given a state , if
For details of DEVS behavior, the readers can refer to behavior of atomic DEVS section.
- Behavior of ping-pong player A
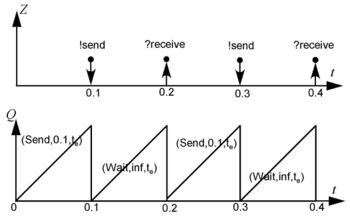
Fig. 3. shows an event segment (top) and the associated state trajectory (bottom) of player A who plays the ping-pong game introduced in Fig. 1. In Fig. 3. the status of player A is described as (state, lifespan, elapsed time)=() and the line segment of the bottom of Fig. 3. denotes the value of the elapsed time. Since the initial state of player A is "Send" and its lifetime is 0.1 seconds, the height of (Send, 0.1, ) is 0.1 which is the value of . After changing into (Wait, inf, 0) when is reset by 0, player A doesn't know when becomes 0 again. However, since player B sends back the ball to player A 0.1 second later, player A gets back to (Send, 0.1 0) at time 0.2. From that time, 0.1 seconds later when player A's status becomes (Send, 0.1, 0.1), player A sends back the ball to player B and gets into (Wait, inf, 0). Thus, this cyclic state transitions which move "Send" to "Wait" back and forth will go forever.

- Behavior of a toaster
Fig. 4. shows an event segment (top) and the associated state trajectory (bottom) of the left slot of the two-slot toaster introduced in Fig. 2. Like Fig.3, the status of the left slot is described as (state, lifespan, elapsed time)=() in Fig. 4. Since the initial state of the toaster is "I" and its lifetime is infinity, the height of (Wait, inf, ) can be determined by when ?push occurs. Fig. 4. illustrates the case ?push happens at time 40 and the toaster changes into (T, 20, 0). From that time, 20 seconds later when its status becomes (T, 20, 20), the toaster gets back to (Wait, inf, 0) where we don't know when it gets back to "Toast" again. Fig. 4. shows the case that ?push occurs at time 90 so the toaster get into (T,20,0). Notice that even though there someone push again at time 97, that status (T, 20, 7) doesn't change at all because (T,?push)=(T,1).
Advantages
Applicability of time-zone abstraction
The property of non-negative rational-valued lifespans which can be preserved or changed by input events along with finite numbers of states and events guarantees that the behavior of FD-DEVS networks can be abstracted as an equivalent finite-vertex reachability graph by abstracting the infinitely-many values of the elapsed times using the time abstracting technique introduced by Prof. D. Dill.[28] An algorithm generating a finite-vertex reachability graph (RG) has been introduced by Zeigler.[25][31]
Reachability graph
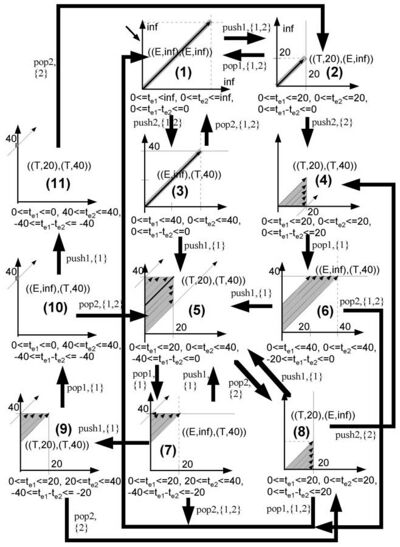
Fig. 5. shows the reachability graph of two-slot toaster which was shown in Fig. 2. In the reachability graph, each vertex has its own discrete state and time zone which are ranges of and . For example, for node (6) of Fig. 5, discrete state information is ((E,),(T,40)), and time zone is . Each directed arch shows how its source vertex changes into the destination vertex along with an associated event and a set of reset models. For example, the transition arc (6) to (5) is triggered by push1 event. At that time, the set {1} of the arc denotes that elapsed time of 1 (that is is reset by 0 when transition (6) to (5) occurs.[25]
Decidability of safety
As a qualitative property, safety of a FD-DEVS network is decidable by (1) generating RG of the given network and (2) checking whether some bad states are reachable or not.[24]
Decidability of liveness
As a qualitative property, liveness of a FD-DEVS network is decidable by (1) generating RG of the given network, (2) from RG, generating kernel directed acyclic graph (KDAG) in which a vertex is strongly connected component, and (3) checking if a vertex of KDAG contains a state transition cycle which contains a set of liveness states.[24]
Disadvantages
Weak expressiveness for describing nondeterminism
The features that all characteristic functions, of FD-DEVS are deterministic can be seen as somehow a limitation to model the system that has non-deterministic behaviors. For example, if a player of the ping-pong game shown in Fig. 1. has a stochastic lifespan at "Send" state, FD-DEVS doesn't capture the non-determinism effectively.
Tool
For verification
There are two open source libraries DEVS# written in C#[32] and XSY written in Python[33] that support some reachability graph-based verification algorithms for finding safeness and liveness.
For simulation via XML
For standardization of DEVS, especially using FDDEVS, Dr. Saurabh Mittal together with co-workers has worked on defining of XML format of FDDEVS.[34] This standard XML format was used for UML execution.[35]
SP-DEVS
SP-DEVS (schedule-preserving discrete event system specification) is a formalism for modeling and analyzing discrete event systems in both simulation and verification ways. SP-DEVS also provides modular and hierarchical modeling features which have been inherited from the classic DEVS.
History
SP-DEVS has been designed to support verification analysis of its networks by guaranteeing to obtain a finite-vertex reachability graph of the original networks, which had been an open problem of DEVS formalism for roughly 30 years. To get such a reachability graph of its networks, SP-DEVS has been imposed the three restrictions:
- finiteness of event sets and state set,
- the lifespan of a state can be scheduled by a rational number or infinity, and
- preserving the internal schedule from any external events.
Thus, SP-DEVS is a sub-class of both DEVS and FD-DEVS. These three restrictions lead that SP-DEVS class is closed under coupling even though the number of states are finite. This property enables a finite-vertex graph-based verification for some qualitative properties and quantitative property, even with SP-DEVS coupled models.
Crosswalk controller example
Consider a crosswalk system. Since a red light (resp. don't-walk light) behaves the opposite way of a green light (resp. walk light), for simplicity, we consider just two lights: a green light (G) and a walk light (W); and one push button as shown in Fig. 1. We want to control two lights of G and W with a set of timing constraints.
To initialize two lights, it takes 0.5 seconds to turn G on and 0.5 seconds later, W gets off. Then, every 30 seconds, there is a chance that G becomes off and W on if someone pushed the push button. For a safety reason, W becomes on two seconds after G got off. 26 seconds later, W gets off and then two seconds later G gets back on. These behaviors repeats.
- Controller Design
To build a controller for above requirements, we can consider one input event 'push-button' (abbreviated by ?p) and four output events 'green-on' (!g:1), 'green-off' (!g:0), 'walk-on' (!w:1) and 'walk-off (!w:0) which will be used as commands signals for the green light and the walk light. As a set of states of the controller, we considers 'booting-green' (BG), 'booting-walk' (BW), 'green-on' (G), 'green-to-red' (GR), 'red-on' (R), 'walk-on' (W), 'delay' (D). Let's design the state transitions as shown in Fig. 2. Initially, the controller starts at BG whose lifespan is 0.5 seconds. After the lifespan, it moves to BW state at this moment, it generates the 'green-on' event, too. After 0.5 seconds staying at BW, it moves to G state whose lifespan is 30 seconds. The controller can keep staying at G by looping G to G without generating any output event or can move to GR state when it receives the external input event ?p. But, the actual staying time at GR is the remaining time for looping at G. From GR, it moves to R state with generating an output event !g:0 and its R state last two seconds then it will move to W state with output event !w:1. 26 seconds later, it moves to D state with generating !w:0 and after staying 2 seconds at D, it moves back to G with output event !g:1.
Atomic SP-DEVS
Formal definition
The above controller for crosswalk lights can be modeled by an atomic SP-DEVS model. Formally, an atomic SP-DEVS is a 7-tuple
where
- is a finite set of input events;
- is a finite set of output events;
- is a finite set of states;
- is the initial state;
- is the time advanced function which defines the lifespan of a state where is the set of non-negative rational numbers plus infinity.
- is the external transition function which defines how an input event changes a state of the system.
- is the output and internal transition function where and denotes the silent event. The output and internal transition function defines how a state generates an output event, at the same time, how the state changes internally.[36]
- Formal representation of crosswalk controller
The above controller shown in Fig. 2 can be written as where ={?p}; ={!g:0, !g:1, !w:0, !w:1}; ={BG, BW, G, GR, R, W, D}; =BG, (BG)=0.5,(BW)=0.5, (G)=30, (GR)=30,(R)=2, (W)=26, (D)=2; (G,?p)=GR, (s,?p)=s if s G; (BG)=(!g:1, BW), (BW)=(!w:0, G),(G)=(, G), (GR)=(!g:0, R), (R)=(!w:1, W), (W)=(!w:0, D), (D)=(!g:1, G);
Behaviors of a SP-DEVS model

To captured the dynamics of an atomic SP-DEVS, we need to introduce two variables associated to time. One is the lifespan, the other is the elapsed time since the last resetting. Let be the lifespan which is not continuously increasing but set by when a discrete event happens. Let denote the elapsed time which is continuously increasing over time if there is no resetting.
Fig.3. shows a state trajectory associated with an event segment of the SP-DEVS model shown in Fig. 2. The top of Fig.3. shows an event trajectory in which the horizontal axis is a time axis so it shows an event occurs at a certain time, for example, !g:1 occurs at 0.5 and !w:0 at 1.0 time unit, and so on. The bottom of Fig. 3 shows the state trajectory associated with the above event segment in which the state is associated with its lifespan and its elapsed time in the form of . For example, (G, 30, 11) denotes that the state is G, its lifespan is and the elapsed time is 11 time units. The line segments of the bottom of Fig. 3 shows the time flow of the elapsed time which is the only one continuous variable in SP-DEVS.
One interesting feature of SF-DEVS might be the preservation of schedule the restriction (3) of SP-DEVS which is drawn at time 47 in Fig. 3. when the external event ?p happens. At this moment, even though the state can change from G to GR, the elapsed time does not change so the line segment is not broken at time 47 and can grow up to which is 30 in this example. Due to this preservation of the schedule from input events as well as the restriction of the time advance to the non-negative rational number (see restriction (2) above), the height of every saw can be a non-negative rational number or infinity (as shown in the bottom of Fig. 3.) in a SP-DEVS model.
- SP-DEVS is a sub-class of DEVS
A SP-DEVS model, is DEVS where
- of are the same as those of .
- Given a state ,
- Given a state and an input event
- Given a state , if
- Given a state , if
Advantages
- Applicability of time-line abstraction
The property of non-negative rational-valued lifespans which are not changed by input events along with finite numbers of states and events guarantees that the behavior of SP-DEVS networks can be abstracted as an equivalent finite-vertex reachability graph by abstracting the infinitely-many values of the elapsed times.
To abstract the infinitely-many cases of elapsed times for each components of SP-DEVS networks, a time-abstraction method, called the time-line abstraction has been introduced in which the orders and relative difference of schedules are preserved.[37][38] By using the time-line abstraction technique, the behavior of any SP-DEVS network can be abstracted as a reachability graph whose numbers of vertices and edges are finite.
- Decidability of safety
As a qualitative property, safety of a SP-DEVS network is decidable by (1) generating the finite-vertex reachability graph of the given network and (2) checking whether some bad states are reachable or not.[37]
- Decidability of liveness
As a qualitative property, liveness of a SP-DEVS network is decidable by (1) generating the finite-vertex reachability graph (RG) of the given network, (2) from RG, generating kernel directed acyclic graph (KDAG) in which a vertex is strongly connected component, and (3) checking if a vertex of KDAG contains a state transition cycle which contains a set of liveness states.[37]
- Decidability of min/max processing time bounds
As a quantitative property, minimum and maximum processing time bounds from two events in SP-DEVS networks can be computed by (1) generating the finite-vertex reachability graph and (2.a) by finding the shortest paths for the minimum processing time bound and (2.b) by finding the longest paths (if available) for the maximum processing time bound.[38]
Disadvantages
- Less expressiveness: OPNA problem
Let a total state of a SP-DEVS model be passive if ; otherwise, it be active.
One of known SP-DEVS's limitation is a phenomenon that "once an SP-DEVS model becomes passive, it never returns to become active (OPNA)". This phenomenon was found first by Hwang,[39] although it was originally called ODNR ("once it dies, it never returns"). The reason why this one happens is because of the restriction (3) above in which no input event can change the schedule so the passive state can not be awaken into the active state.
For example, the toaster models drawn in Fig. 3(b) are not SP-DEVS because the total state associated with "idle" (I), is passive but it moves to an active state, "toast" (T) whose toasting time is 20 seconds or 40 seconds. Actually, the model shown in Fig. 3(b) is FD-DEVS.
Tools
There is an open source library, called DEVS#[32] that supports some algorithms for finding safeness and liveness as well as min/max processing time bounds.
See also
DEVS-related articles
Other formalisms
- Automata theory: a formal method for state transition systems
- Finite-state machine: a state transition machine with finite sets of events and states
- Petri nets: a graphical representation of state and transition relations
- Markov chain: a stochastic process in which the future will be determined by the current state
- Specification and Description Language: SDL, a formal complete and unambiguous language to graphically represent simulation models.
References
- ↑ 1.0 1.1 Zeigler, Bernard (1976). Theory of Modeling and Simulation (1st ed.). New York: Wiley Interscience. ISBN 0-12-778455-1. http://acims.asu.edu/publications/books-proceedings-and-manuscripts/theory-of-modeling-and-simulation-2nd-edition-academic-press.
- ↑ Zeigler, Bernard (1968). On the Feedback Complexity of Automata (Ph.D.). University of Michigan.automata were the mathematical models of Dr. Zeigler's Ph.D. thesis
- ↑ 3.0 3.1 3.2 3.3 Zeigler, Bernard (1984). Multifacetted Modeling and Discrete Event Simulation. London; Orlando: Academic Press. ISBN 978-0-12-778450-2.
- ↑ Zeigler, Bernard (1987). "Hierarchical, modular discrete-event modelling in an object-oriented environment". Simulation 49 (5): 219–230. doi:10.1177/003754978704900506.
- ↑ Zeigler, Bernard; Kim, Tag Gon; Praehofer, Herbert (2000). Theory of Modeling and Simulation (2nd ed.). New York: Academic Press. ISBN 978-0-12-778455-7.
- ↑ We can also define the external transition function as where such that for a total state , is a partial state, is the lifespan of , and is the elapsed time since last update of . For more how to understand this function, refer to the article, Behavior of DEVS.
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedZeigler904 - ↑ Cellier, Francois E. (1991). Continuous System Modeling (1st ed.). Springer. ISBN 978-0-387-97502-3.
- ↑ Cellier, Francois E.; Kofman, Ernesto (2006). Continuous System Simulation (1st ed.). Springer. ISBN 978-0-387-26102-7.
- ↑ Nutaro, James (2010). Building Software for Simulation: Theory, Algorithms, and Applications in C++ (1st ed.). Wiley. ISBN 978-0-470-41469-9.
- ↑ the use of quantized values in order to simulate continuous systems by means of a discrete event method was empirically tried out a few years sooner - in the early 1990s - by a French engineer. He was then working for a company spun off from University of Valenciennes, and now part of the Schneider Electric. This quantization is a feature of a simulation software of which this engineer is the conceptor and main developer, that is used for PLC programs checking and operator training.
- ↑ Hwang, M.H.; Zeigler, B.P. (2009). "Reachability Graph of Finite and Deterministic DEVS Networks". IEEE Transactions on Automation Science and Engineering 6 (3): 454–467. doi:10.1109/TASE.2009.2024064.
- ↑ 13.0 13.1 Hwang, M.H.. "Qualitative verification of finite and real-time DEVS networks". Proceedings of 2012 Symposium on Theory of Modeling and Simulation - DEVS Integrative M&S Symposium.
- ↑ Hwang, M.H. (April 2–8, 2005). "Tutorial: Verification of Real-time System Based on Schedule-Preserved DEVS". Proceedings of 2005 DEVS Symposium. San Diego. ISBN 1-56555-293-8.
- ↑ Hwang, M.H.; Zeigler, B.P.. "A Modular Verification Framework using Finite and Deterministic DEVS". Proceedings of 2006 DEVS Symposium. Huntsville, Alabama, USA. pp. 57–65.
- ↑ Zeigler, Bernard (1976). Theory of Modeling and Simulation (first ed.). New York: Wiley Interscience.
- ↑ Zeigler, Bernard; Kim, Tag Gon; Praehofer, Herbert (2000). Theory of Modeling and Simulation (second ed.). New York: Academic Press. ISBN 978-0-12-778455-7.
- ↑ Hwang, Moon H. (2012). "Qualitative Verification of Finite and Real-Time DEVS Networks". Proceedings of 2012 TMS/DEVS. Orlando, FL, USA. pp. 43:1–43:8. ISBN 978-1-61839-786-7.
- ↑ Giambiasi, N.; Escude, B.; Ghosh, S. (2001). "Generalized Discrete Event Simulation of Dynamic Systems". SCS Transactions: Recent Advances in DEVS Methodology-part II 18 (4): 216–229.
- ↑ Zacharewicz, Gregory; Frydman, Claudia; Giambiasi, Norbert (2008). "G-DEVS/HLA Environment for Distributed Simulations of Workflows". Simulation 84 (5): 197–213. doi:10.1177/0037549708092833. https://hal.archives-ouvertes.fr/hal-00204203/file/Revue_Simulation_GZ_CF_NG_Reviewed_Final_SAGE_Biblio%281%29.pdf.
- ↑ Wainer, Gabriel A. (2009). Discrete-Event Modeling and Simulation: A Practitioner's Approach (1st ed.). CRC Press. ISBN 978-1-4200-5336-4.
- ↑ 22.0 22.1 Zeigler, Bernard; Kim, Tag Gon; Praehofer, Herbert (2000). Theory of Modeling and Simulation (second ed.). New York: Academic Press. ISBN 978-0-12-778455-7.
- ↑ 23.0 23.1 Zeigler, Bernard (1984). Multifacetted Modeling and Discrete Event Simulation. London; Orlando: Academic Press. ISBN 978-0-12-778450-2.
- ↑ 24.0 24.1 24.2 24.3 24.4 Hwang, M. H.; Zeigler, Bernard (2006). "A Reachable Graph of Finite and Deterministic DEVS Networks". Proceedings of 2006 DEVS Symposium. Huntsville, Alabama, USA. pp. 48–56. http://www.acims.arizona.edu/.
- ↑ 25.0 25.1 25.2 25.3 25.4 Hwang, M. H.; Zeigler, Bernard (2009). "Reachability Graph of Finite & Deterministic DEVS". IEEE Transactions on Automation Science and Engineering 6 (3): 454–467. doi:10.1109/TASE.2009.2024064. https://ieeexplore.ieee.org/document/5071137.
- ↑ Zeigler, Bernard; Kim, Tag Gon; Praehofer, Herbert (2000). Theory of Modeling and Simulation (second ed.). New York: Academic Press. ISBN 978-0-12-778455-7.
- ↑ 27.0 27.1 Hwang, M. H. (August 2005). "Generating Finite-State Global Behavior of Reconfigurable Automation Systems: DEVS Approach". Proceedings of 2005 IEEE-CASE. Edmonton, Canada. http://moonho.hwang.googlepages.com/publications.
- ↑ 28.0 28.1 Dill, D. L. (1989). "Timing Assumptions and Verification of Finite-State Concurrent Systems". Proceedings of the Workshop on Computer Aided Verification Methods for Finite State Systems. Grenoble, France. pp. 197–212.
- ↑ Hwang, M. H. (August 2005). "Generating Finite-State Global Behavior of Reconfigurable Automation Systems: DEVS Approach". Proceedings of 2005 IEEE-CASE. Edmonton, Canada. http://moonho.hwang.googlepages.com/publications. (note: can be divided into two functions: and )
- ↑ Zeigler, Bernard; Kim, Tag Gon; Praehofer, Herbert (2000). Theory of Modeling and Simulation (second ed.). New York: Academic Press. ISBN 978-0-12-778455-7. (note: can be divided into two functions: and )
- ↑ Hwang, M. H.; Zeigler, Bernard (2006). "A Modular Verification Framework using Finite and Deterministic DEVS". Proceedings of 2006 DEVS Symposium. Huntsville, Alabama, USA. pp. 57–65. http://www.acims.arizona.edu/.
- ↑ 32.0 32.1 "DEVSsharp". https://xsy-csharp.sourceforge.net/DEVSsharp/.
- ↑ "XSY". https://code.google.com/p/x-s-y/.
- ↑ Mittal, Saurabh. "xFDDEVS". http://www.duniptechnologies.com/research/xfddevs/.
- ↑ Risco-Martín, José L.; de la Cruz, Jesús M.; Mittal, Saurabh; Zeigler, Bernard (2009). "eUDEVS: Executable UML with DEVS Theory of Modeling and Simulation". SIMULATION, Transaction of the Society for Modeling and Simulation International 85 (11–12): 750–777. doi:10.1177/0037549709104727. http://sim.sagepub.com/content/85/11-12/750.short.
- ↑ Zeigler, Bernard; Kim, Tag Gon; Praehofer, Herbert (2000). Theory of Modeling and Simulation (second ed.). New York: Academic Press. ISBN 978-0-12-778455-7. (note: can be divided into two functions: and )
- ↑ 37.0 37.1 37.2 Hwang, M. H. (April 2–8, 2005). "Tutorial: Verification of Real-time System Based on Schedule-Preserved DEVS". Proceedings of 2005 DEVS Symposium. San Diego. ISBN 978-1-56555-293-7. http://moonho.hwang.googlepages.com/publications.
- ↑ 38.0 38.1 Hwang, M. H.; Cho, S. K.; Zeigler, Bernard; Lin, F. (2007). Processing Time Bounds of Schedule-Preserving DEVS (Report). http://www.acims.arizona.edu/. Retrieved 2008-03-18.
- ↑ Hwang, M. H. (August 1–2, 2005). "Generating Finite-State Global Behavior of Reconfigurable Automation Systems: DEVS Approach". Proceedings of 2005 IEEE-CASE. Edmonton, Canada. http://moonho.hwang.googlepages.com/publications.
 |
 KSF
KSF