Defective coloring

In graph theory, a mathematical discipline, coloring refers to an assignment of colours or labels to vertices, edges and faces of a graph. Defective coloring is a variant of proper vertex coloring. In a proper vertex coloring, the vertices are coloured such that no adjacent vertices have the same colour. In defective coloring, on the other hand, vertices are allowed to have neighbours of the same colour to a certain extent. (See here for Glossary of graph theory)

History

Defective coloring was introduced nearly simultaneously by Burr and Jacobson, Harary and Jones and Cowen, Cowen and Woodall.^[1] Surveys of this and related colorings are given by Marietjie Frick.^[2] Cowen, Cowen and Woodall ^[1] focused on graphs embedded on surfaces and gave a complete characterization of all k and d such that every planar is (k, d)-colorable. Namely, there does not exist a d such that every planar graph is (1, d)- or (2, d)-colorable; there exist planar graphs which are not (3, 1)-colorable, but every planar graph is (3, 2)-colorable. Together with the (4, 0)-coloring implied by the four color theorem, this solves defective chromatic number for the plane. Poh ^[3] and Goddard ^[4] showed that any planar graph has a special (3,2)-coloring in which each color class is a linear forest, and this can be obtained from a more general result of Woodall. For general surfaces, it was shown that for each genus [math]\displaystyle{ g \geq 0 }[/math], there exists a [math]\displaystyle{ k=k(g) }[/math] such that every graph on the surface of genus [math]\displaystyle{ g }[/math] is (4, k)-colorable.^[1] This was improved to (3, k)-colorable by Dan Archdeacon.^[5] For general graphs, a result of László Lovász from the 1960s, which has been rediscovered many times ^[6][7][8] provides a O(∆E)-time algorithm for defective coloring graphs of maximum degree ∆.

Definitions and terminology

Defective coloring

A (k, d)-coloring of a graph G is a coloring of its vertices with k colours such that each vertex v has at most d neighbours having the same colour as the vertex v. We consider k to be a positive integer (it is inconsequential to consider the case when k = 0) and d to be a non-negative integer. Hence, (k, 0)-coloring is equivalent to proper vertex coloring.^[9]

d-defective chromatic number

The minimum number of colours k required for which G is (k, d)-colourable is called the d-defective chromatic number, [math]\displaystyle{ \chi_d (G) }[/math].^[10]

For a graph class G, the defective chromatic number of G is minimum integer k such that for some integer d, every graph in G is (k,d)-colourable. For example, the defective chromatic number of the class of planar graphs equals 3, since every planar graph is (3,2)-colourable and for every integer d there is a planar graph that is not (2,d)-colourable.

Impropriety of a vertex

Let c be a vertex-coloring of a graph G. The impropriety of a vertex v of G with respect to the coloring c is the number of neighbours of v that have the same color as v. If the impropriety of v is 0, then v is said to be properly colored.^[1]

Impropriety of a vertex-coloring

Let c be a vertex-coloring of a graph G. The impropriety of c is the maximum of the improprieties of all vertices of G. Hence, the impropriety of a proper vertex coloring is 0.^[1]

Example

Example of defective colouring of a cycle on five vertices when d = 0, 1, 2

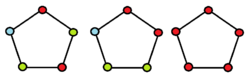
An example of defective colouring of a cycle on five vertices, [math]\displaystyle{ C_5 }[/math], is as shown in the figure. The first subfigure is an example of proper vertex colouring or a (k, 0)-coloring. The second subfigure is an example of a (k, 1)-coloring and the third subfigure is an example of a (k, 2)-coloring. Note that,

[math]\displaystyle{ \chi_0 (C_5) = \chi (C_5) = 3 }[/math]

[math]\displaystyle{ \chi_1 (C_5) = 3 }[/math]

[math]\displaystyle{ \chi_2 (C_n) = 1; \forall n \in \mathbb{N} }[/math]

Properties

• It is enough to consider connected graphs, as a graph G is (k, d)-colourable if and only if every connected component of G is (k, d)-colourable.^[1]
• In graph theoretic terms, each colour class in a proper vertex coloring forms an independent set, while each colour class in a defective coloring forms a subgraph of degree at most d.^[11]
• If a graph is (k, d)-colourable, then it is (k′, d′)-colourable for each pair (k′, d′) such that k′ ≥ k and d′≥ d.^[1]

Some results

Every outerplanar graph is (2,2)-colorable

Proof: Let [math]\displaystyle{ G }[/math] be a connected outerplanar graph. Let [math]\displaystyle{ v_0 }[/math] be an arbitrary vertex of [math]\displaystyle{ G }[/math]. Let [math]\displaystyle{ V_i }[/math] be the set of vertices of [math]\displaystyle{ G }[/math] that are at a distance [math]\displaystyle{ i }[/math] from [math]\displaystyle{ v_0 }[/math]. Let [math]\displaystyle{ G_i }[/math] be [math]\displaystyle{ \langle V_i \rangle }[/math], the subgraph induced by [math]\displaystyle{ V_i }[/math]. Suppose [math]\displaystyle{ G_i }[/math] contains a vertex of degree 3 or more, then it contains [math]\displaystyle{ K_{1,3} }[/math] as a subgraph. Then we contract all edges of [math]\displaystyle{ V_0 \cup V_1 \cup ... \cup V_{i-1} }[/math] to obtain a new graph [math]\displaystyle{ G' }[/math]. It is to be noted that [math]\displaystyle{ \langle V_0 \cup V_1 \cup ... \cup V_{i-1} \rangle }[/math] of [math]\displaystyle{ G' }[/math] is connected as every vertex in [math]\displaystyle{ V_i }[/math] is adjacent to a vertex in [math]\displaystyle{ V_{i-1} }[/math]. Hence, by contracting all the edges mentioned above, we obtain [math]\displaystyle{ G' }[/math] such that the subgraph [math]\displaystyle{ \langle V_0 \cup V_1 \cup ... \cup V_{i-1} \rangle }[/math] of [math]\displaystyle{ G' }[/math] is replaced by a single vertex that is adjacent to every vertex in [math]\displaystyle{ V_i }[/math]. Thus [math]\displaystyle{ G' }[/math] contains [math]\displaystyle{ K_{2,3} }[/math] as a subgraph. But every subgraph of an outerplanar graph is outerplanar and every graph obtained by contracting edges of an outerplanar graph is outerplanar. This implies that [math]\displaystyle{ K_{2,3} }[/math] is outerplanar, a contradiction. Hence no graph [math]\displaystyle{ G_i }[/math] contains a vertex of degree 3 or more, implying that [math]\displaystyle{ G }[/math] is (k, 2)-colorable. No vertex of [math]\displaystyle{ V_i }[/math] is adjacent to any vertex of [math]\displaystyle{ V_{i-1} }[/math] or [math]\displaystyle{ V_{i+1}, i \geqslant 1 }[/math], hence the vertices of [math]\displaystyle{ V_i }[/math] can be colored blue if [math]\displaystyle{ i }[/math] is odd and red if even. Hence, we have produced a (2,2)-coloring of [math]\displaystyle{ G }[/math].^[1]

Corollary: Every planar graph is (4,2)-colorable. This follows as if [math]\displaystyle{ G }[/math] is planar then every [math]\displaystyle{ G_i }[/math] (same as above) is outerplanar. Hence every [math]\displaystyle{ G_i }[/math] is (2,2)-colourable. Therefore, each vertex of [math]\displaystyle{ V_i }[/math] can be colored blue or red if [math]\displaystyle{ i }[/math] is even and green or yellow if [math]\displaystyle{ i }[/math] is odd, hence producing a (4,2)-coloring of [math]\displaystyle{ G }[/math].

Graphs excluding a complete minor

For every integer [math]\displaystyle{ t }[/math] there is an integer [math]\displaystyle{ N }[/math] such that every graph [math]\displaystyle{ G }[/math] with no [math]\displaystyle{ K_t }[/math] minor is [math]\displaystyle{ (t-1,N) }[/math]-colourable.^[12]

Computational complexity

Defective coloring is computationally hard. It is NP-complete to decide if a given graph [math]\displaystyle{ G }[/math] admits a (3,1)-coloring, even in the case where [math]\displaystyle{ G }[/math] is of maximum vertex-degree 6 or planar of maximum vertex-degree 7.^[13]

Applications

An example of an application of defective colouring is the scheduling problem where vertices represent jobs (say users on a computer system), and edges represent conflicts (needing to access one or more of the same files). Allowing a defect means tolerating some threshold of conflict: each user may find the maximum slowdown incurred for retrieval of data with two conflicting other users on the system acceptable, and with more than two unacceptable.^[14]

Notes

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Defective coloring. Read more