Density (polytope)

The boundary of the regular enneagram {9/4} winds around its centre 4 times, so it has a density of 4.

In geometry, the density of a star polyhedron is a generalization of the concept of winding number from two dimensions to higher dimensions, representing the number of windings of the polyhedron around the center of symmetry of the polyhedron. It can be determined by passing a ray from the center to infinity, passing only through the facets of the polytope and not through any lower dimensional features, and counting how many facets it passes through. For polyhedra for which this count does not depend on the choice of the ray, and for which the central point is not itself on any facet, the density is given by this count of crossed facets.

The same calculation can be performed for any convex polyhedron, even one without symmetries, by choosing any point interior to the polyhedron as its center. For these polyhedra, the density will be 1. More generally, for any non-self-intersecting (acoptic) polyhedron, the density can be computed as 1 by a similar calculation that chooses a ray from an interior point that only passes through facets of the polyhedron, adds one when this ray passes from the interior to the exterior of the polyhedron, and subtracts one when this ray passes from the exterior to the interior of the polyhedron. However, this assignment of signs to crossings does not generally apply to star polyhedra, as they do not have a well-defined interior and exterior.

Tessellations with overlapping faces can similarly define density as the number of coverings of faces over any given point.^[1]

Polygons

The density of a polygon is the number of times that the polygonal boundary winds around its center. For convex polygons, and more generally simple polygons (not self-intersecting), the density is 1, by the Jordan curve theorem.

The density of a polygon can also be called its turning number; the sum of the turn angles of all the vertices divided by 360°. This will be an integer for all unicursal paths in a plane.

The density of a compound polygon is the sum of the densities of the component polygons.

Regular star polygons

For a regular star polygon {p/q}, the density is q. It can be visually determined by counting the minimum number of edge crossings of a ray from the center to infinity.

Examples

• 

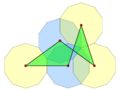
  A single-crossing polygon, like this equilateral pentagon, has density 0.

• 

  Regular pentagon {5} has density 1.

• 

  Isotoxal tetradecagon, {(7/2)_α}, has density 2, similar to regular {7/2}.

• 

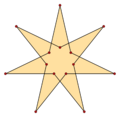
  Heptagram {7/3} has density 3.

• 

  Isotoxal hexagram (compound) 2{(3/2)_α} has density 4.

• 

  Isotoxal dodecagram, {(6/5)_α}, has density 5, similar to regular {12/5}.

Polyhedra

A polyhedron and its dual have the same density.

Total curvature

A polyhedron can be considered a surface with Gaussian curvature concentrated at the vertices and defined by an angle defect. The density of a polyhedron is equal to the total curvature (summed over all its vertices) divided by 4π.^[2]

For example, a cube has 8 vertices, each with 3 squares, leaving an angle defect of π/2. 8×π/2=4π. So the density of the cube is 1.

Simple polyhedra

The density of a polyhedron with simple faces and vertex figures is half of the Euler Characteristic, χ. If its genus is g, its density is 1-g.

χ = V − E + F = 2D = 2(1-g).

• 

  Density of topological sphere polyhedron is one, like a cube.
  v=8, e=12, f=6.

• 

  Density of a genus 1 toroidal polyhedron is zero, like this hexagonal form:
  v=24, e=48, f=24.

• 

  Density of a genus 5 toroidal is -4, like this Stewart toroid:
  v=72, e=168, f=88.

Regular star polyhedra

Arthur Cayley used density as a way to modify Euler's polyhedron formula (V − E + F = 2) to work for the regular star polyhedra, where d_v is the density of a vertex figure, d_f of a face and D of the polyhedron as a whole:

[math]\displaystyle{ d_v v - e + d_{f} f = 2 D }[/math]^[3]

For example, the great icosahedron, {3, 5/2}, has 20 triangular faces (d_f = 1), 30 edges and 12 pentagrammic vertex figures (d_v = 2), giving

2·12 − 30 + 1·20 = 14 = 2D.

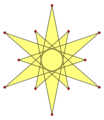
This implies a density of 7. The unmodified Euler's polyhedron formula fails for the small stellated dodecahedron {5/2, 5} and its dual great dodecahedron {5, 5/2}, for which V − E + F = −6.

The regular star polyhedra exist in two dual pairs, with each figure having the same density as its dual: one pair (small stellated dodecahedron—great dodecahedron) has a density of 3, while the other (great stellated dodecahedron–great icosahedron) has a density of 7.

The nonconvex great icosahedron, {3,5/2} has a density of 7 as demonstrated in this transparent and cross-sectional view on the right.

General star polyhedra

Edmund Hess generalized the formula for star polyhedra with different kinds of face, some of which may fold backwards over others. The resulting value for density corresponds to the number of times the associated spherical polyhedron covers the sphere.

[math]\displaystyle{ \sum_{ i} d_{vi} v_i - e + \sum_{ i} d_{fi} f_i = 2 D }[/math]

This allowed Coxeter et al. to determine the densities of the majority of the uniform polyhedra, which have one vertex type, and multiple face types.^[4]

• 

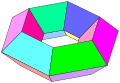
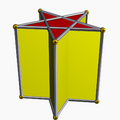
  The density of an octagonal prism, wrapped twice is 2, {8/2}×{}, shown here with offset vertices for clarity.
  v=16, e=24
  f₁=8 {4}, f₂=2 {8/2}
  with d_f1=1, d_f2=2, d_v=1.

• 

  The density of a pentagrammic prism, {5/2}×{} is 2.
  v=10, e=15,
  f₁=5 {4}, f₂=2 {5/2},
  d_f1=1, d_f2=2.

Nonorientable polyhedra

For hemipolyhedra, some of whose faces pass through the center, the density cannot be defined. Non-orientable polyhedra also do not have well-defined densities.

Regular 4-polytopes

The great grand stellated 120-cell has density 191.

There are 10 regular star 4-polytopes (called the Schläfli–Hess 4-polytopes), which have densities between 4, 6, 20, 66, 76, and 191. They come in dual pairs, with the exception of the self-dual density-6 and density-66 figures.

Notes

References

• Coxeter, H. S. M.; Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN:0-486-61480-8
• Coxeter, H. S. M.; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 246 (916): 401–450, doi:10.1098/rsta.1954.0003, ISSN 0080-4614 
• Wenninger, Magnus J. (1979), "An introduction to the notion of polyhedral density", Spherical models, CUP Archive, pp. 132–134, ISBN 978-0-521-22279-2 

External links

• Weisstein, Eric W.. "Polygon density". http://mathworld.wolfram.com/PolygonDensity.html. 

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Density (polytope). Read more