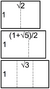
E (mathematical constant)

Template:Infobox mathematical constant

Graph of the equation y = 1/x. Here, e is the unique number larger than 1 that makes the shaded area under the curve equal to 1.

Part of a series of articles on the
mathematical constant e
Properties
Natural logarithm Exponential function
Applications
compound interest Euler's identity Euler's formula half-lives exponential growth and decay
Defining e
proof that e is irrational representations of e Lindemann–Weierstrass theorem
People
John Napier Leonhard Euler
Related topics
Schanuel's conjecture
v t e

The number e is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of natural logarithms. It is the limit of (1 + 1/n)ⁿ as n approaches infinity, an expression that arises in the computation of compound interest. It can also be calculated as the sum of the infinite series [math]\displaystyle{ e = \sum\limits_{n = 0}^{\infty} \frac{1}{n!} = 1 + \frac{1}{1} + \frac{1}{1\cdot 2} + \frac{1}{1\cdot 2\cdot 3} + \cdots. }[/math]

It is also the unique positive number a such that the graph of the function y = a^x has a slope of 1 at x = 0.

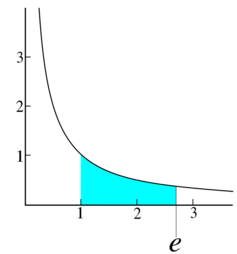
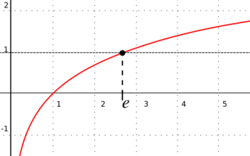
The (natural) exponential function f(x) = e^x is the unique function f that equals its own derivative and satisfies the equation f(0) = 1; hence one can also define e as f(1). The natural logarithm, or logarithm to base e, is the inverse function to the natural exponential function. The natural logarithm of a number k > 1 can be defined directly as the area under the curve y = 1/x between x = 1 and x = k, in which case e is the value of k for which this area equals 1 (see image). There are various other characterizations.

The number e is sometimes called Euler's number, after the Swiss mathematician Leonhard Euler, though this can invite confusion with Euler's constant, a different constant typically denoted [math]\displaystyle{ \gamma }[/math]. Alternatively, e can be called Napier's constant after John Napier.^[1][2] The constant was discovered by the Swiss mathematician Jacob Bernoulli while studying compound interest.^[3][4]

The number e is of great importance in mathematics,^[5] alongside 0, 1, π, and i. All five appear in one formulation of Euler's identity [math]\displaystyle{ e^{i\pi}+1=0 }[/math] and play important and recurring roles across mathematics.^[6][7] Like the constant π, e is irrational, meaning that it cannot be represented as a ratio of integers, and moreover it is transcendental, meaning that it is not a root of any non-zero polynomial with rational coefficients.^[2] To 40 decimal places, the value of e is:^[8]

History

The first references to the constant were published in 1618 in the table of an appendix of a work on logarithms by John Napier. However, this did not contain the constant itself, but simply a list of logarithms to the base [math]\displaystyle{ e }[/math]. It is assumed that the table was written by William Oughtred. In 1661, Christiaan Huygens studied how to compute logarithms by geometrical methods and calculated a quantity that, in retrospect, is the base-10 logarithm of e, but he did not recognize e itself as a quantity of interest.^[4][9]

The constant itself was introduced by Jacob Bernoulli in 1683, for solving the problem of continuous compounding of interest.^[10][11] In his solution, the constant e occurs as the limit [math]\displaystyle{ \lim_{n\to \infty} \left( 1 + \frac{1}{n} \right)^n, }[/math] where n represents the number of intervals in a year on which the compound interest is evaluated (for example, [math]\displaystyle{ n=12 }[/math] for monthly compounding).

The first symbol used for this constant was the letter b by Gottfried Leibniz in letters to Christiaan Huygens in 1690 and 1691.^[12]

Leonhard Euler started to use the letter e for the constant in 1727 or 1728, in an unpublished paper on explosive forces in cannons,^[13] and in a letter to Christian Goldbach on 25 November 1731.^[14][15] The first appearance of e in a printed publication was in Euler's Mechanica (1736).^[16] It is unknown why Euler chose the letter e.^[17] Although some researchers used the letter c in the subsequent years, the letter e was more common and eventually became standard.^[1]

Euler proved that e is the sum of the infinite series [math]\displaystyle{ e = \sum_{n = 0}^\infty \frac{1}{n!} = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \cdots , }[/math] where n! is the factorial of n.^[4] The equivalence of the two characterizations using the limit and the infinite series can be proved via the binomial theorem.^[18]

Applications

Compound interest

The effect of earning 20% annual interest on an initial $1,000 investment at various compounding frequencies. The limiting curve on top is the graph [math]\displaystyle{ y=1000e^{0.2t} }[/math], where y is in dollars, t in years, and 0.2 = 20%.

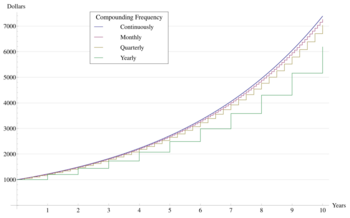
Jacob Bernoulli discovered this constant in 1683, while studying a question about compound interest:^[4]

An account starts with $1.00 and pays 100 percent interest per year. If the interest is credited once, at the end of the year, the value of the account at year-end will be $2.00. What happens if the interest is computed and credited more frequently during the year?

If the interest is credited twice in the year, the interest rate for each 6 months will be 50%, so the initial $1 is multiplied by 1.5 twice, yielding $1.00 × 1.5² = $2.25 at the end of the year. Compounding quarterly yields $1.00 × 1.25⁴ = $2.44140625, and compounding monthly yields $1.00 × (1 + 1/12)¹² = $2.613035.... If there are n compounding intervals, the interest for each interval will be 100%/n and the value at the end of the year will be $1.00 × (1 + 1/n)ⁿ.^[19][20]

Bernoulli noticed that this sequence approaches a limit (the force of interest) with larger n and, thus, smaller compounding intervals.^[4] Compounding weekly (n = 52) yields $2.692596..., while compounding daily (n = 365) yields $2.714567... (approximately two cents more). The limit as n grows large is the number that came to be known as e. That is, with continuous compounding, the account value will reach $2.718281828... More generally, an account that starts at $1 and offers an annual interest rate of R will, after t years, yield e^Rt dollars with continuous compounding. Here, R is the decimal equivalent of the rate of interest expressed as a percentage, so for 5% interest, R = 5/100 = 0.05.^[19][20]

Bernoulli trials

Graphs of probability P of not observing independent events each of probability 1/n after n Bernoulli trials, and 1 − P  vs n ; it can be observed that as n increases, the probability of a 1/n-chance event never appearing after n tries rapidly converges to 1/e.

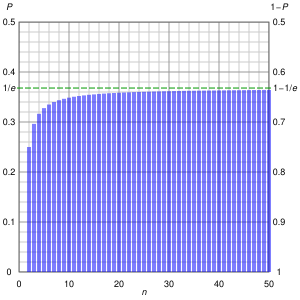
The number e itself also has applications in probability theory, in a way that is not obviously related to exponential growth. Suppose that a gambler plays a slot machine that pays out with a probability of one in n and plays it n times. As n increases, the probability that gambler will lose all n bets approaches 1/e. For n = 20, this is already approximately 1/2.789509....

This is an example of a Bernoulli trial process. Each time the gambler plays the slots, there is a one in n chance of winning. Playing n times is modeled by the binomial distribution, which is closely related to the binomial theorem and Pascal's triangle. The probability of winning k times out of n trials is:^[21]

[math]\displaystyle{ \Pr[k~\mathrm{wins~of}~n] = \binom{n}{k} \left(\frac{1}{n}\right)^k\left(1 - \frac{1}{n}\right)^{n-k}. }[/math]

In particular, the probability of winning zero times (k = 0) is

[math]\displaystyle{ \Pr[0~\mathrm{wins~of}~n] = \left(1 - \frac{1}{n}\right)^{n}. }[/math]

The limit of the above expression, as n tends to infinity, is precisely 1/e.

Exponential growth and decay

Exponential growth is a process that increases quantity over time at an ever-increasing rate. It occurs when the instantaneous rate of change (that is, the derivative) of a quantity with respect to time is proportional to the quantity itself.^[20] Described as a function, a quantity undergoing exponential growth is an exponential function of time, that is, the variable representing time is the exponent (in contrast to other types of growth, such as quadratic growth). If the constant of proportionality is negative, then the quantity decreases over time, and is said to be undergoing exponential decay instead. The law of exponential growth can be written in different but mathematically equivalent forms, by using a different base, for which the number e is a common and convenient choice: [math]\displaystyle{ x(t) = x_0\cdot e^{kt} = x_0\cdot e^{t/\tau}. }[/math] Here, [math]\displaystyle{ x_0 }[/math] denotes the initial value of the quantity x, k is the growth constant, and [math]\displaystyle{ \tau }[/math] is the time it takes the quantity to grow by a factor of e.

Standard normal distribution

Main page: Normal distribution

The normal distribution with zero mean and unit standard deviation is known as the standard normal distribution,^[22] given by the probability density function [math]\displaystyle{ \phi(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2} x^2}. }[/math]

The constraint of unit standard deviation (and thus also unit variance) results in the 1/2 in the exponent, and the constraint of unit total area under the curve [math]\displaystyle{ \phi(x) }[/math] results in the factor [math]\displaystyle{ \textstyle 1/\sqrt{2\pi} }[/math]. This function is symmetric around x = 0, where it attains its maximum value [math]\displaystyle{ \textstyle 1/\sqrt{2\pi} }[/math], and has inflection points at x = ±1.

Derangements

Main page: Derangement

Another application of e, also discovered in part by Jacob Bernoulli along with Pierre Remond de Montmort, is in the problem of derangements, also known as the hat check problem:^[23] n guests are invited to a party and, at the door, the guests all check their hats with the butler, who in turn places the hats into n boxes, each labelled with the name of one guest. But the butler has not asked the identities of the guests, and so puts the hats into boxes selected at random. The problem of de Montmort is to find the probability that none of the hats gets put into the right box. This probability, denoted by [math]\displaystyle{ p_n\! }[/math], is:

[math]\displaystyle{ p_n = 1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \cdots + \frac{(-1)^n}{n!} = \sum_{k = 0}^n \frac{(-1)^k}{k!}. }[/math]

As n tends to infinity, p_n approaches 1/e. Furthermore, the number of ways the hats can be placed into the boxes so that none of the hats are in the right box is n!/e, rounded to the nearest integer, for every positive n.^[24]

Optimal planning problems

The maximum value of [math]\displaystyle{ \sqrt[x]{x} }[/math] occurs at [math]\displaystyle{ x = e }[/math]. Equivalently, for any value of the base b > 1, it is the case that the maximum value of [math]\displaystyle{ x^{-1}\log_b x }[/math] occurs at [math]\displaystyle{ x = e }[/math] (Steiner's problem, discussed below).

This is useful in the problem of a stick of length L that is broken into n equal parts. The value of n that maximizes the product of the lengths is then either^[25]

[math]\displaystyle{ n = \left\lfloor \frac{L}{e} \right\rfloor }[/math] or [math]\displaystyle{ \left\lceil \frac{L}{e} \right\rceil. }[/math]

The quantity [math]\displaystyle{ x^{-1}\log_b x }[/math] is also a measure of information gleaned from an event occurring with probability [math]\displaystyle{ 1/x }[/math], so that essentially the same optimal division appears in optimal planning problems like the secretary problem.

Asymptotics

The number e occurs naturally in connection with many problems involving asymptotics. An example is Stirling's formula for the asymptotics of the factorial function, in which both the numbers e and π appear:^[26] [math]\displaystyle{ n! \sim \sqrt{2\pi n} \left(\frac{n}{e}\right)^n. }[/math]

As a consequence,^[26] [math]\displaystyle{ e = \lim_{n\to\infty} \frac{n}{\sqrt[n]{n!}} . }[/math]

Properties

Calculus

The graphs of the functions x ↦ a^x are shown for a = 2 (dotted), a = e (blue), and a = 4 (dashed). They all pass through the point (0,1), but the red line (which has slope 1) is tangent to only e^x there.

The value of the natural log function for argument e, i.e. ln e, equals 1.

The principal motivation for introducing the number e, particularly in calculus, is to perform differential and integral calculus with exponential functions and logarithms.^[27] A general exponential function y = a^x has a derivative, given by a limit:

[math]\displaystyle{ \begin{align} \frac{d}{dx}a^x &= \lim_{h\to 0}\frac{a^{x+h} - a^x}{h} = \lim_{h\to 0}\frac{a^x a^h - a^x}{h} \\ &= a^x \cdot \left(\lim_{h\to 0}\frac{a^h - 1}{h}\right). \end{align} }[/math]

The parenthesized limit on the right is independent of the variable x. Its value turns out to be the logarithm of a to base e. Thus, when the value of a is set to e, this limit is equal to 1, and so one arrives at the following simple identity:

[math]\displaystyle{ \frac{d}{dx}e^x = e^x. }[/math]

Consequently, the exponential function with base e is particularly suited to doing calculus. Choosing e (as opposed to some other number) as the base of the exponential function makes calculations involving the derivatives much simpler.

Another motivation comes from considering the derivative of the base-a logarithm (i.e., log_a x),^[27] for x > 0:

[math]\displaystyle{ \begin{align} \frac{d}{dx}\log_a x &= \lim_{h\to 0}\frac{\log_a(x + h) - \log_a(x)}{h} \\ &= \lim_{h\to 0}\frac{\log_a(1 + h/x)}{x\cdot h/x} \\ &= \frac{1}{x}\log_a\left(\lim_{u\to 0}(1 + u)^\frac{1}{u}\right) \\ &= \frac{1}{x}\log_a e, \end{align} }[/math]

where the substitution u = h/x was made. The base-a logarithm of e is 1, if a equals e. So symbolically,

[math]\displaystyle{ \frac{d}{dx}\log_e x = \frac{1}{x}. }[/math]

The logarithm with this special base is called the natural logarithm, and is denoted as ln; it behaves well under differentiation since there is no undetermined limit to carry through the calculations.

Thus, there are two ways of selecting such special numbers a. One way is to set the derivative of the exponential function a^x equal to a^x, and solve for a. The other way is to set the derivative of the base a logarithm to 1/x and solve for a. In each case, one arrives at a convenient choice of base for doing calculus. It turns out that these two solutions for a are actually the same: the number e.

The five colored regions are of equal area, and define units of hyperbolic angle along the hyperbola [math]\displaystyle{ xy=1. }[/math]

The Taylor series for the exponential function can be deduced from the facts that the exponential function is its own derivative and that it equals 1 when evaluated at 0:^[28] [math]\displaystyle{ e^x = \sum_{n=0}^\infty \frac{x^n}{n!}. }[/math] Setting [math]\displaystyle{ x = 1 }[/math] recovers the definition of e as the sum of an infinite series.

The natural logarithm function can be defined as the integral from 1 to [math]\displaystyle{ x }[/math] of [math]\displaystyle{ 1/t }[/math], and the exponential function can then be defined as the inverse function of the natural logarithm. The number e is the value of the exponential function evaluated at [math]\displaystyle{ x = 1 }[/math], or equivalently, the number whose natural logarithm is 1. It follows that e is the unique positive real number such that [math]\displaystyle{ \int_1^e \frac{1}{t} \, dt = 1. }[/math]

Because e^x is the unique function (up to multiplication by a constant K) that is equal to its own derivative,

[math]\displaystyle{ \frac{d}{dx}Ke^x = Ke^x, }[/math]

it is therefore its own antiderivative as well:^[29]

[math]\displaystyle{ \int Ke^x\,dx = Ke^x + C . }[/math]

Equivalently, the family of functions

[math]\displaystyle{ y(x) = Ke^x }[/math]

where K is any real or complex number, is the full solution to the differential equation

[math]\displaystyle{ y' = y . }[/math]

Inequalities

Exponential functions y = 2^x and y = 4^x intersect the graph of y = x + 1, respectively, at x = 1 and x = -1/2. The number e is the unique base such that y = e^x intersects only at x = 0. We may infer that e lies between 2 and 4.

The number e is the unique real number such that [math]\displaystyle{ \left(1 + \frac{1}{x}\right)^x \lt e \lt \left(1 + \frac{1}{x}\right)^{x+1} }[/math] for all positive x.^[30]

Also, we have the inequality [math]\displaystyle{ e^x \ge x + 1 }[/math] for all real x, with equality if and only if x = 0. Furthermore, e is the unique base of the exponential for which the inequality a^x ≥ x + 1 holds for all x.^[31] This is a limiting case of Bernoulli's inequality.

Exponential-like functions

The global maximum of ^x√x occurs at x = e.

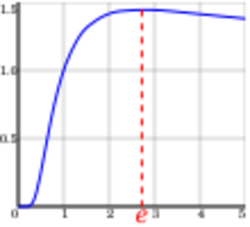
Steiner's problem asks to find the global maximum for the function

[math]\displaystyle{ f(x) = x^\frac{1}{x} . }[/math]

This maximum occurs precisely at x = e. (One can check that the derivative of ln f(x) is zero only for this value of x.)

Similarly, x = 1/e is where the global minimum occurs for the function

[math]\displaystyle{ f(x) = x^x . }[/math]

The infinite tetration

[math]\displaystyle{ x^{x^{x^{\cdot^{\cdot^{\cdot}}}}} }[/math] or [math]\displaystyle{ {^\infty}x }[/math]

converges if and only if x ∈ [(1/e)^e, e^1/e] ≈ [0.06599, 1.4447] ,^[32][33] shown by a theorem of Leonhard Euler.^[34][35][36]

Number theory

The real number e is irrational. Euler proved this by showing that its simple continued fraction expansion does not terminate.^[37] (See also Fourier's proof that e is irrational.)

Furthermore, by the Lindemann–Weierstrass theorem, e is transcendental, meaning that it is not a solution of any non-zero polynomial equation with rational coefficients. It was the first number to be proved transcendental without having been specifically constructed for this purpose (compare with Liouville number); the proof was given by Charles Hermite in 1873.^[38]

It is conjectured that e is normal, meaning that when e is expressed in any base the possible digits in that base are uniformly distributed (occur with equal probability in any sequence of given length).^[39]

In algebraic geometry, a period is a number that can be expressed as an integral of an algebraic function over an algebraic domain. The constant π is a period, but it is conjectured that e is not.^[40]

Complex numbers

The exponential function e^x may be written as a Taylor series

[math]\displaystyle{ e^{x} = 1 + {x \over 1!} + {x^{2} \over 2!} + {x^{3} \over 3!} + \cdots = \sum_{n=0}^{\infty} \frac{x^n}{n!}. }[/math]

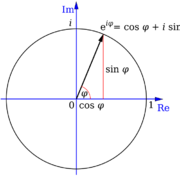
Because this series is convergent for every complex value of x, it is commonly used to extend the definition of e^x to the complex numbers.^[41] This, with the Taylor series for sin and cos x, allows one to derive Euler's formula:

[math]\displaystyle{ e^{ix} = \cos x + i\sin x , }[/math]

which holds for every complex x.^[41] The special case with x = π is Euler's identity:

[math]\displaystyle{ e^{i\pi} + 1 = 0 , }[/math] which is considered to be an exemplar of mathematical beauty as it shows a profound connection between the most fundamental numbers in mathematics. In addition, it is directly used in a proof that π is transcendental, which implies the impossibility of squaring the circle.^[42][43] Moreover, the identity implies that, in the principal branch of the logarithm,^[41]

[math]\displaystyle{ \ln (-1) = i\pi . }[/math]

Furthermore, using the laws for exponentiation,

[math]\displaystyle{ (\cos x + i\sin x)^n = \left(e^{ix}\right)^n = e^{inx} = \cos (nx) + i \sin (nx) , }[/math]

which is de Moivre's formula.^[44]

The expressions of cos x and sin x in terms of the exponential function can be deduced from the Taylor series:^[41] [math]\displaystyle{ \cos x = \frac{e^{ix} + e^{-ix}}{2} , \qquad \sin x = \frac{e^{ix} - e^{-ix}}{2i}. }[/math]

The expression [math]\displaystyle{ \cos x + i \sin x }[/math] is sometimes abbreviated as cis(x).^[44]

Representations

The number e can be represented in a variety of ways: as an infinite series, an infinite product, a continued fraction, or a limit of a sequence. In addition to the limit and the series given above, there is also the continued fraction

[math]\displaystyle{ e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, ..., 1, 2n, 1, ...], }[/math]^[45][46]

which written out looks like

[math]\displaystyle{ e = 2 + \cfrac{1} {1 + \cfrac{1} {2 + \cfrac{1} {1 + \cfrac{1} {1 + \cfrac{1} {4 + \cfrac{1} {1 + \cfrac{1} {1 + \ddots} } } } } } } . }[/math]

The following infinite product evaluates to e:^[25] [math]\displaystyle{ e = \frac{2}{1} \left(\frac{4}{3}\right)^{1/2} \left(\frac{6 \cdot 8}{5 \cdot 7}\right)^{1/4} \left(\frac{10 \cdot 12 \cdot 14 \cdot 16}{9 \cdot 11 \cdot 13 \cdot 15}\right)^{1/8} \cdots. }[/math]

Many other series, sequence, continued fraction, and infinite product representations of e have been proved.

Stochastic representations

In addition to exact analytical expressions for representation of e, there are stochastic techniques for estimating e. One such approach begins with an infinite sequence of independent random variables X₁, X₂..., drawn from the uniform distribution on [0, 1]. Let V be the least number n such that the sum of the first n observations exceeds 1:

[math]\displaystyle{ V = \min\left\{ n \mid X_1 + X_2 + \cdots + X_n \gt 1 \right\}. }[/math]

Then the expected value of V is e: E(V) = e.^[47][48]

Known digits

The number of known digits of e has increased substantially during the last decades. This is due both to the increased performance of computers and to algorithmic improvements.^[49][50]

Since around 2010, the proliferation of modern high-speed desktop computers has made it feasible for amateurs to compute trillions of digits of e within acceptable amounts of time. On Dec 5, 2020, a record-setting calculation was made, giving e to 31,415,926,535,897 (approximately π×10¹³) digits.^[56]

Computing the digits

One way to compute the digits of e is with the series^[57] [math]\displaystyle{ e=\sum_{k=0}^\infty \frac{1}{k!}. }[/math]

A faster method involves two recursive functions [math]\displaystyle{ p(a,b) }[/math] and [math]\displaystyle{ q(a,b) }[/math]. The functions are defined as [math]\displaystyle{ \binom{p(a,b)}{q(a,b)}= \begin{cases} \binom{1}{b}, & \text{if }b=a+1\text{,} \\ \binom{p(a,m)q(m,b)+p(m,b)}{q(a,m)q(m,b)}, & \text{otherwise, where }m=\lfloor(a+b)/2\rfloor .\end{cases} }[/math]

The expression [math]\displaystyle{ 1+\frac{p(0,n)}{q(0,n)} }[/math] produces the nth partial sum of the series above. This method uses binary splitting to compute e with fewer single-digit arithmetic operations and thus reduced bit complexity. Combining this with fast Fourier transform-based methods of multiplying integers makes computing the digits very fast.^[57]

In computer culture

During the emergence of internet culture, individuals and organizations sometimes paid homage to the number e.

In an early example, the computer scientist Donald Knuth let the version numbers of his program Metafont approach e. The versions are 2, 2.7, 2.71, 2.718, and so forth.^[58]

In another instance, the IPO filing for Google in 2004, rather than a typical round-number amount of money, the company announced its intention to raise 2,718,281,828 USD, which is e billion United States dollar rounded to the nearest dollar.^[59]

Google was also responsible for a billboard^[60] that appeared in the heart of Silicon Valley, and later in Cambridge, Massachusetts; Seattle, Washington; and Austin, Texas . It read "{first 10-digit prime found in consecutive digits of e}.com". The first 10-digit prime in e is 7427466391, which starts at the 99th digit.^[61] Solving this problem and visiting the advertised (now defunct) website led to an even more difficult problem to solve, which consisted in finding the fifth term in the sequence 7182818284, 8182845904, 8747135266, 7427466391. It turned out that the sequence consisted of 10-digit numbers found in consecutive digits of e whose digits summed to 49. The fifth term in the sequence is 5966290435, which starts at the 127th digit.^[62] Solving this second problem finally led to a Google Labs webpage where the visitor was invited to submit a résumé.^[63]

References

Further reading

• Maor, Eli; e: The Story of a Number, ISBN 0-691-05854-7
• Commentary on Endnote 10 of the book Prime Obsession for another stochastic representation
• McCartin, Brian J. (2006). "e: The Master of All". The Mathematical Intelligencer 28 (2): 10–21. doi:10.1007/bf02987150. http://www.maa.org/sites/default/files/pdf/upload_library/22/Chauvenet/mccartin.pdf. 

External links

• The number e to 1 million places and NASA.gov 2 and 5 million places
• e Approximations – Wolfram MathWorld
• Earliest Uses of Symbols for Constants Jan. 13, 2008
• "The story of e", by Robin Wilson at Gresham College, 28 February 2007 (available for audio and video download)
• e Search Engine 2 billion searchable digits of e, π and √2

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/E (mathematical constant). Read more