Apparent wind

V = boat speed, H = head wind, W = true wind, A = apparent wind, α = pointing angle, β = angle of apparent wind

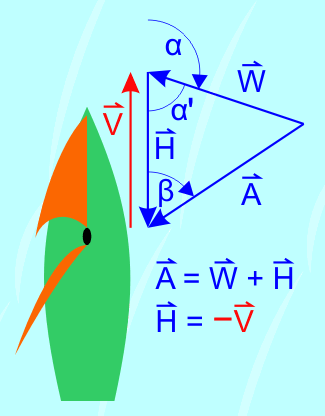
Apparent wind is the wind experienced by a moving object.

Definition of apparent wind

The apparent wind is the wind experienced by an observer in motion and is the relative velocity of the wind in relation to the observer.^{[citation needed]}

The velocity of the apparent wind is the vector sum of the velocity of the headwind (which is the velocity a moving object would experience in still air) plus the velocity of the true wind. The headwind is the additive inverse of the object's velocity; therefore, the velocity of the apparent wind can also be defined as a vector sum of the velocity of the true wind minus the velocity of the object.^{[citation needed]}

Apparent wind in sailing

In sailing, apparent wind is the speed and direction of wind indicated by a wind instrument (anemometer) on a moving craft (on water, land or ice) in undisturbed air. It is composed of the combined speeds and directions of the craft and wind observed by a stationary wind instrument—the true wind. A true wind coming from the bow increases the apparent wind induced by the speed of the craft, coming from the stern it decreases apparent wind, and coming from the side the apparent wind angle and speed change according to the combined speed and direction of each the craft and the true wind. Apparent wind is important to sailors in order to set sail angle with respect to the wind and to anticipate how much power the wind will generate on a point of sail. Apparent wind differs in speed and direction from the true wind that is experienced by a stationary observer and composed of the true wind speed (TWS) and true wind direction (TWD) or the TWS and true wind angle (TWA) relative to the boat if it were stationary.^[1] In nautical terminology, apparent wind is measured in knots and degrees.

Note that a number of additional factors come into play when converting the measurements from the masthead anemometer into the true wind if a high degree of accuracy is required, including the following:^[2][3][4]

• Leeway (or drift on power vessels) - it is very seldom that a craft is pointing in the direction it is going, and on a sailboat the angle of leeway is the difference between the heading of the craft and its actual track through the water. This must be corrected for when converting apparent wind angle to true wind direction. The same effect is found when the craft is altering course.
• Mast twist - the rigging loads often put a significant amount of torsion on the mast, especially if the rig has runners, so it is twisted along its length
• Mast rotation - many racing multihulls have a mast that can be rotated, so the anemometer reading needs to be corrected by the angle of rotation of the mast
• Heel angle - this is a simple trigonometric correction
• Upwash from the sails - the airflow around the top of the mast is distorted by the presence of the sails. This effect varies with the sails set at the time, the wind speed and the point of sail, but is noticed by the true wind angle changing from port to starboard tack, and the true wind speed changing from when beating to running
• Boat motions - as the masthead is so distant from the centre of motion of the craft, inertial effect on both the wind vane and the anemometer cups can be significant when the craft is moving, especially when pitching and rolling
• Wind shear - there can be a significant change in both wind speed and direction between the water's surface and the top of the mast, especially in conditions of unstable, light airs. The wind instruments are just measuring conditions at the masthead, and these are not necessarily the same at all heights

In the presence of a current, the true wind is considered to be that measured on the craft drifting with the water over the bottom, and wind with respect to the sea bed as the ground or geographical wind.^{[citation needed]}

Instruments

The apparent wind on board (a boat) is often quoted as a speed measured by a masthead transducer containing an anemometer and wind vane that measures wind speed in knots and wind direction in degrees relative to the heading of the boat. Modern instrumentation can calculate the true wind velocity when the apparent wind and boat speed and direction are input.^{[citation needed]}

Implications on sailing speeds

In sailboat racing, and especially in speed sailing, apparent wind is a vital factor, when determining the points of sail a sailboat can effectively travel in. A vessel traveling at increasing speed relative to the prevailing wind will encounter the wind driving the sail at a decreasing angle and increasing velocity. Eventually, the increased drag and diminished degree of efficiency of a sail at extremely low angles will cause a loss of accelerating force. This constitutes the main limitation to the speed of wind-driven vessels and vehicles.^{[citation needed]}

Windsurfers and certain types of boats are able to sail faster than the true wind. These include fast multihulls and some planing monohulls. Ice-sailors and land-sailors also usually fall into this category, because of their relatively low amount of drag or friction.^{[citation needed]}

In the foiling AC72 America's cup catamarans, the boats sail through the water at up to double the environmental wind strength. The effect of this is to radically change the apparent wind direction when sailing "downwind". In these boats the forward speed is so great that the apparent wind is always forward—at an angle that varies between 2 and 4 degrees to the wing sail. This means that AC72's are effectively tacking downwind, although at a greater angle than the normal 45-degree upwind angle, usually between 50 and 70 degrees.^[5]

Other areas of relevance

In fixed-wing aircraft, apparent wind is what is experienced on board, and it determines the necessary speeds for take-off and landing. Aircraft carriers generally steam directly upwind at maximum speed, in order to increase apparent wind and reduce the necessary take-off velocity. Land-based airport traffic, as well as most mid-sized and large birds generally take off and land facing upwind for the same reason.^{[citation needed]}

Calculating apparent velocity and angle

[math]\displaystyle{ A = \sqrt{W^2 + V^2 + 2WV\cos{\alpha}} }[/math]

Where:

• [math]\displaystyle{ V }[/math] = velocity (boat speed over ground, always ≥ 0)
• [math]\displaystyle{ W }[/math] = true wind velocity (always ≥ 0)
• [math]\displaystyle{ \alpha }[/math] = true pointing angle in degrees (0 = upwind, 180 = downwind)
• [math]\displaystyle{ A }[/math] = apparent wind velocity (always ≥ 0)

The above formula is derived from the Law of cosines and using [math]\displaystyle{ \cos(\alpha') = \cos(180^\circ-\alpha) = -\cos(\alpha) }[/math].

The angle of apparent wind ([math]\displaystyle{ \beta }[/math]) can be calculated from the measured velocity of the boat and wind using the inverse cosine in degrees ([math]\displaystyle{ \arccos }[/math])

[math]\displaystyle{ \beta = \arccos \left( \frac{W\cos \alpha+V}{A} \right) = \arccos \left( \frac{W\cos \alpha+V}{\sqrt{W^2 + V^2 +2WV\cos{\alpha}}} \right) }[/math]

If the velocity of the boat and the velocity and the angle of the apparent wind are known, for instance from a measurement, the true wind velocity and direction can be calculated with:

[math]\displaystyle{ W = \sqrt{A^2 + V^2 - 2AV\cos{\beta}} }[/math]

and

[math]\displaystyle{ \alpha = \arccos \left( \frac{A\cos \beta-V}{W} \right) = \arccos \left( \frac{A\cos \beta-V}{\sqrt{A^2 + V^2 -2AV\cos{\beta}}} \right) }[/math]

Note: Due to quadrant ambiguity, this equation for [math]\displaystyle{ \alpha }[/math] is only valid when the apparent winds are coming from the starboard direction (0° < β < 180°). For port apparent winds (180° < β < 360° or 0° > β > -180°), the true pointing angle (α) has the opposite sign:

[math]\displaystyle{ \alpha = -\arccos \left( \frac{A\cos \beta-V}{W} \right) = -\arccos \left( \frac{A\cos \beta-V}{\sqrt{A^2 + V^2 -2AV\cos{\beta}}} \right) }[/math]

References

External links

• http://www.csgnetwork.com/twscorcalc.html
• https://www.tecepe.com.br/nav/inav_c11.htm.

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Apparent wind. Read more