Degree of curvature

Short description: Measure of a bend's roundness

Degree of curve or degree of curvature is a measure of curvature of a circular arc used in civil engineering for its easy use in layout surveying.

Definition

The degree of curvature is defined as the central angle to the ends of an agreed length of either an arc or a chord;^[1] various lengths are commonly used in different areas of practice. This angle is also the change in forward direction as that portion of the curve is traveled. In an n-degree curve, the forward bearing changes by n degrees over the standard length of arc or chord.

Usage

Curvature is usually measured in radius of curvature. A small circle can be easily laid out by just using radius of curvature, but degree of curvature is more convenient for calculating and laying out the curve if the radius is large as a kilometer or a mile, as it needed for large scale works like roads and railroads. By using degrees of curvature, curve setting can be easily done with the help of a transit or theodolite and a chain, tape, or rope of a prescribed length.

Length selection

The usual distance used to compute degree of curvature in North American road work is 100 feet (30.5 m) of arc.^[2]^{[page needed]} Conversely, North American railroad work traditionally used 100 feet of chord, which is used in other places^[where?] for road work. Other lengths may be used—such as 100 metres (330 ft) where SI is favoured or a shorter length for sharper curves. Where degree of curvature is based on 100 units of arc length, the conversion between degree of curvature and radius is $Dr = 18000/π \approx 5729.57795$ , where $D$ is degree and $r$ is radius.

Since rail routes have very large radii, they are laid out in chords, as the difference to the arc is inconsequential; this made work easier before electronic calculators became available.

The 100 feet (30.48 m) is called a station, used to define length along a road or other alignment, annotated as stations plus feet 1+00, 2+00, etc. Metric work may use similar notation, such as kilometers plus meters 1+000.

Formulas for radius of curvature

Diagram showing different parts of the curve used in the formula

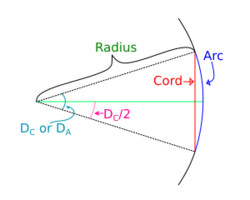
Degree of curvature can be converted to radius of curvature by the following formulae:

Formula from arc length

[math]\displaystyle{ r = \frac{180^\circ A}{\pi D_\text{C}} }[/math]

where [math]\displaystyle{ A }[/math] is arc length, [math]\displaystyle{ r }[/math] is radius of curvature, and [math]\displaystyle{ D_\text{C} }[/math] is degree of curvature, arc definition

Substitute deflection angle for degree of curvature or make arc length equal to 100 feet.

Formula from chord length

[math]\displaystyle{ r = \frac{C}{2 \sin \left( \frac{D_\text{C}}{2} \right) } }[/math]

where [math]\displaystyle{ C }[/math] is chord length, [math]\displaystyle{ r }[/math] is radius of curvature and [math]\displaystyle{ D_\text{C} }[/math] is degree of curvature, chord definition

Formula from radius

[math]\displaystyle{ D_\text{C} = 5729.58/r }[/math]

Example

As an example, a curve with an arc length of 600 units that has an overall sweep of 6 degrees is a 1-degree curve: For every 100 feet of arc, the bearing changes by 1 degree. The radius of such a curve is 5729.57795. If the chord definition is used, each 100-unit chord length will sweep 1 degree with a radius of 5729.651 units, and the chord of the whole curve will be slightly shorter than 600 units.

References

↑ Wolf; Ghilani (2006), Elementary Surveying (11th ed.), ISBN 9780131481893
↑ Davis, Raymond Earl; Foote, Francis Seeley; Kelly, Joe Wallace (1966) (in en). Surveying Theory and Practice. McGraw-Hill. ISBN 978-0-07-015812-2.

External links

0.00

(0 votes)

Original source: https://en.wikipedia.org/wiki/Degree of curvature. Read more

[1] Wolf; Ghilani (2006), Elementary Surveying (11th ed.), ISBN 9780131481893

[2] Davis, Raymond Earl; Foote, Francis Seeley; Kelly, Joe Wallace (1966) (in en). Surveying Theory and Practice. McGraw-Hill. ISBN 978-0-07-015812-2.

[1]

[2]