Hallade method

Sine, cosine, and versine of θ in terms of a unit circle, centered at O

The Hallade method, devised by Frenchman Emile Hallade, is a method used in track geometry for surveying, designing and setting out curves in railway track.^[1]

It involves measuring the offset of a string line from the outside of a curve at the central point of a chord. In reality, string is too thick to provide a clear reading and breaks easily under the tension needed to minimise movement due to wind. A reel of wire may be used instead, with special holders (Hallade forks) employed to hold the wire at a fixed distance from the rail. The measurement is taken with a Hallade rule, a specialist ruler whose zero point matches the offset of the forks, thus cancelling it out. The purpose of the offset is to allow small negative measurements. Without this, surveyors would frequently have to read from both sides of the rail to determine the correct values on straight sections of track which typically feature a mix of small positive and negative versines.

A standard chord length is used: in the UK this is conventionally 30 metres, or sometimes 20 metres. Half chords, i.e. 15 metre or 10 metre intervals, are marked on the datum rail using chalk. The string, which is one full chord long, is then held taut with one end on two marks at each end of a chord, and the offset at the half chord mark measured.

The versine of the chord, which is equal to this measured offset value can be calculated using the approximation of:

[math]\displaystyle{ \operatorname{versin} \theta = 1 - cos\,\theta }[/math]

which is:

[math]\displaystyle{ v\approx\frac{L^2}{8r} }[/math]

where
[math]\displaystyle{ v }[/math] = versine (m),
[math]\displaystyle{ L }[/math] = chord length (m),
[math]\displaystyle{ r }[/math] = radius of curve (m)

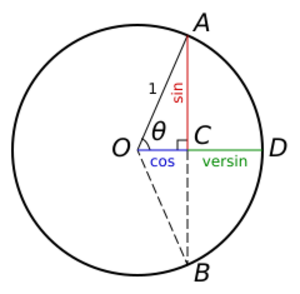
This formula is also true for other units of measurement such as in feet. The relationship of versine, chord and radius is derived from the Pythagorean theorem. Based on the diagram on the right:

[math]\displaystyle{ OC = \sqrt{OA^2 - AC^2} }[/math]

We can replace OC with r (radius) minus v, OA with r and AC with L/2 (half a chord). Then the rearrange formula to:

[math]\displaystyle{ r - v = \sqrt{r^2 - (\frac{L}{2})^2}, }[/math]

[math]\displaystyle{ r^2 - 2rv + v^2 = r^2 - (\frac{L}{2})^2, }[/math]

[math]\displaystyle{ 2r - v = \frac{L^2}{4v}, }[/math]

[math]\displaystyle{ r=\frac{L^2}{8v}+ \frac{v}{2}. }[/math]

Since the curved tracks are usually large, the result of v/2 is very small. To simplify the formula, the approximation is:

[math]\displaystyle{ r\approx\frac{L^2}{8v} }[/math]

The following can be used to find the versine of a given constant radius curve:^[2]

[math]\displaystyle{ v\approx\frac{L^2}{8r} }[/math]

The Hallade method is to use the chord to continuously measure the versine in an overlapping pattern along the curve. The versine values for the perfect circular curve would have the same number.^[3] By comparing the surveyed versine figures to the design versines, this can then be used to determine what slues should be applied to the track in order to make the curve correctly aligned. This is often done using pegs which are driven into the ground in the cess beside the track to be aligned. The process of putting the pegs in the correct positions is known as 'setting out'. If the curve needs to be of a desired constant radius, which will usually be determined by physical obstructions and the degree of cant which is permitted, the versine can be calculated for the desired radius using this approximation. In practice, many track curves are transition curves and so have changing radii. In order to maintain a smooth transition, the differences in versines between consecutive half chords are measured and minimised.

The Hallade survey is a survey method that uses the same principle to measure the versines along an existing curve. Based on the versine values, the radius of that circular curved track can be approximated to:^[4]

[math]\displaystyle{ r\approx\frac{L^2}{8v} }[/math]

This method can be done manually, and this method is still used in the UK. However, due to the complexity of the calculations over long lengths of track, it is now often done by computer,^[5] with the track geometry data being loaded straight onto a computer controlled tamping and lining machine for implementation.

See also

• Track geometry
• Track geometry car

References

External links

• The Hallade System
• Railway engineers

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Hallade method. Read more