Navigation function

Navigation function usually refers to a function of position, velocity, acceleration and time which is used to plan robot trajectories through the environment. Generally, the goal of a navigation function is to create feasible, safe paths that avoid obstacles while allowing a robot to move from its starting configuration to its goal configuration.

Potential functions as navigation functions

A potential function. Imagine dropping a marble on the surface. It will avoid the three obstacles and eventually reach the goal position in the center.

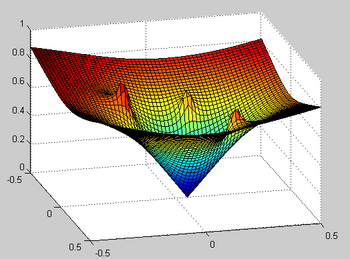
Potential functions assume that the environment or work space is known. Obstacles are assigned a high potential value, and the goal position is assigned a low potential. To reach the goal position, a robot only needs to follow the negative gradient of the surface.

We can formalize this concept mathematically as following: Let [math]\displaystyle{ X }[/math] be the state space of all possible configurations of a robot. Let [math]\displaystyle{ X_g \subset X }[/math] denote the goal region of the state space.

Then a potential function [math]\displaystyle{ \phi(x) }[/math] is called a (feasible) navigation function if ^[1]

1. [math]\displaystyle{ \phi(x)=0\ \forall x \in X_g }[/math]
2. [math]\displaystyle{ \phi(x) = \infty }[/math] if and only if no point in [math]\displaystyle{ {X_{g}} }[/math] is reachable from [math]\displaystyle{ x }[/math].
3. For every reachable state, [math]\displaystyle{ x \in X \setminus {X_{g}} }[/math], the local operator produces a state [math]\displaystyle{ x' }[/math] for which [math]\displaystyle{ \phi(x') \lt \phi(x) }[/math].

Probabilistic navigation function

Probabilistic navigation function is an extension of the classical navigation function for static stochastic scenarios. The function is defined by permitted collision probability, which limits the risk during motion. The Minkowski sum used for in the classical definition is replaced with a convolution of the geometries and the Probability Density Functionss of locations. Denoting the target position by [math]\displaystyle{ x_d }[/math], the Probabilistic navigation function is defined as:^[2] [math]\displaystyle{ {\varphi}(x) = \frac{\gamma_d (x)}{{{{\left[ {\gamma_d^{K}(x) + \beta \left( x \right)} \right]}^{\frac{1}{K}}}}} }[/math] where [math]\displaystyle{ K }[/math] is a predefined constant like in the classical navigation function, which ensures the Morse nature of the function. [math]\displaystyle{ \gamma_d(x) }[/math] is the distance to the target position [math]\displaystyle{ {{||x - {x_d}|{|^2}}} }[/math], and [math]\displaystyle{ \beta \left( x \right) }[/math] takes into account all obstacles, defined as [math]\displaystyle{ \beta \left( x \right) = \prod\limits_{i = 0}^{{N_{o}}} {{\beta _i}\left( x \right)} }[/math] where [math]\displaystyle{ \beta _i(x) }[/math] is based on the probability for a collision at location [math]\displaystyle{ x }[/math]. The probability for a collision is limited by a predetermined value [math]\displaystyle{ \Delta }[/math], meaning: [math]\displaystyle{ \beta _i (x) = \Delta- p^i\left( x \right) }[/math] and, [math]\displaystyle{ \beta _0 (x)= - \Delta + p^0\left( x \right) }[/math]

where [math]\displaystyle{ p^i(x) }[/math] is the probability to collide with the i-th obstacle. A map [math]\displaystyle{ \varphi }[/math] is said to be a probabilistic navigation function if it satisfies the following conditions:

1. It is a navigation function.
2. The probability for a collision is bounded by a predefined probability [math]\displaystyle{ \Delta }[/math].

Navigation Function in Optimal Control

While for certain applications, it suffices to have a feasible navigation function, in many cases it is desirable to have an optimal navigation function with respect to a given cost functional [math]\displaystyle{ J }[/math]. Formalized as an optimal control problem, we can write

[math]\displaystyle{ \text{minimize } J(x_{1:T},u_{1:T})=\int\limits_T L(x_t,u_t,t) dt }[/math]

[math]\displaystyle{ \text{subject to } \dot{x_t} = f(x_t,u_t) }[/math]

whereby [math]\displaystyle{ x }[/math] is the state, [math]\displaystyle{ u }[/math] is the control to apply, [math]\displaystyle{ L }[/math] is a cost at a certain state [math]\displaystyle{ x }[/math] if we apply a control [math]\displaystyle{ u }[/math], and [math]\displaystyle{ f }[/math] models the transition dynamics of the system.

Applying Bellman's principle of optimality the optimal cost-to-go function is defined as

[math]\displaystyle{ \displaystyle \phi(x_t) = \min_{u_t \in U(x_t)} \Big\{ L(x_t,u_t) + \phi(f(x_t,u_t)) \Big\} }[/math]

Together with the above defined axioms we can define the optimal navigation function as

1. [math]\displaystyle{ \phi(x)=0\ \forall x \in X_g }[/math]
2. [math]\displaystyle{ \phi(x) = \infty }[/math] if and only if no point in [math]\displaystyle{ {X_{G}} }[/math] is reachable from [math]\displaystyle{ x }[/math].
3. For every reachable state, [math]\displaystyle{ x \in X \setminus {X_{G}} }[/math], the local operator produces a state [math]\displaystyle{ x' }[/math] for which [math]\displaystyle{ \phi(x') \lt \phi(x) }[/math].
4. [math]\displaystyle{ \displaystyle \phi(x_t) = \min_{u_t \in U(x_t)} \Big\{ L(x_t,u_t) + \phi(f(x_t,u_t)) \Big\} }[/math]

Even if a navigation function is an example for reactive control, it can be utilized for optimal control problems as well which includes planning capabilities.^[3]

Stochastic Navigation Function

If we assume the transition dynamics of the system or the cost function as subjected to noise, we obtain a stochastic optimal control problem with a cost [math]\displaystyle{ J(x_t,u_t) }[/math] and dynamics [math]\displaystyle{ f }[/math]. In the field of reinforcement learning the cost is replaced by a reward function [math]\displaystyle{ R(x_t,u_t) }[/math] and the dynamics by the transition probabilities [math]\displaystyle{ P(x_{t+1}|x_t,u_t) }[/math].

See also

• Control Theory
• Optimal Control
• Robot Control
• Motion Planning
• Reinforcement Learning

References

Sources

• LaValle, Steven M. (2006), Planning Algorithms (First ed.), Cambridge University Press, ISBN 978-0-521-86205-9, http://planning.cs.uiuc.edu/ 
• Laumond, Jean-Paul (1998), Robot Motion Planning and Control (First ed.), Springer, ISBN 3-540-76219-1, http://homepages.laas.fr/jpl/book-toc.html 

External links

• NFsim: MATLAB Toolbox for motion planning using Navigation Functions.

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Navigation function. Read more