Thermal simulations for integrated circuits

Miniaturizing components has always been a primary goal in the semiconductor industry because it cuts production cost and lets companies build smaller computers and other devices. Miniaturization, however, has increased dissipated power per unit area and made it a key limiting factor in integrated circuit performance. Temperature increase becomes relevant for relatively small-cross-sections wires, where it may affect normal semiconductor behavior. Besides, since the generation of heat is proportional to the frequency of operation for switching circuits, fast computers have larger heat generation than slow ones, an undesired effect for chips manufacturers. This article summaries physical concepts that describe the generation and conduction of heat in an integrated circuit, and presents numerical methods that model heat transfer from a macroscopic point of view.

Generation and transfer of heat

Fourier's law

At macroscopic level, Fourier's law states a relation between the transmitted heat per unit time per unit area and the gradient of temperature:

[math]\displaystyle{ q= - \kappa \nabla T }[/math]

Where [math]\displaystyle{ \kappa }[/math] is the thermal conductivity, [W·m⁻¹ K⁻¹].

Joule heating

Electronic systems work based on current and voltage signals. Current is the flow of charged particles through the material and these particles (electrons or holes), interact with the lattice of the crystal losing its energy which is released in form of heat. Joule Heating is a predominant mechanism for heat generation in integrated circuits^[1] and is an undesired effect in most of the cases. For an ohmic material, it has the form:

[math]\displaystyle{ Q = j^{2} \rho }[/math]

Where [math]\displaystyle{ j }[/math] is the current density in [A·m⁻²], [math]\displaystyle{ \rho }[/math] is the specific electric resistivity in [[math]\displaystyle{ {\Omega} }[/math]·m] and [math]\displaystyle{ Q }[/math] is the generated heat per unit volume in [W·m⁻³].^[1]

Heat-transfer equation

The governing equation of the physics of the heat transfer problem relates the flux of heat in space, its variation in time and the generation of power by the following expression:

[math]\displaystyle{ \nabla\left(\kappa\left( T\right) \nabla T\right)+g=\rho C\frac{\partial T}{\partial t} }[/math]

Where [math]\displaystyle{ \kappa }[/math] is the thermal conductivity, [math]\displaystyle{ \rho }[/math] is the density of the medium, [math]\displaystyle{ C }[/math] is the specific heat, [math]\displaystyle{ \alpha=\frac{\kappa}{\rho C} }[/math], the thermal diffusivity and [math]\displaystyle{ g }[/math] is the rate of heat generation per unit volume. Heat diffuses from the source following the above equation and solution in an homogeneous medium follows a Gaussian distribution.

Techniques to solve heat equation

Kirchhoff transformation

To get rid of the temperature dependence of [math]\displaystyle{ \kappa }[/math], Kirchhoff transformation can be performed ^[2]

[math]\displaystyle{ \theta=T_{s}+\frac{1}{\kappa_{s}}\int_{T_{s}}^{T}\kappa(T)dT }[/math]

where [math]\displaystyle{ \kappa_{s} = \kappa\left( T_{s}\right) }[/math] and [math]\displaystyle{ T_{s} }[/math] is the heat sink temperature. When applying this transformation, the heat equation becomes:

[math]\displaystyle{ \alpha\nabla^{2}\theta+\frac{\alpha}{\kappa_{s}}g=\frac{\partial\theta}{\partial t} }[/math]

where [math]\displaystyle{ \alpha=\frac{\kappa}{\rho C} }[/math] is called the diffusivity,^[2] which also depends on the temperature. To completely linearize the equation, a second transformation is employed:

[math]\displaystyle{ \alpha_{s}\tau=\int_{0}^{t}\alpha(\theta)dt }[/math]

yielding the expression:

[math]\displaystyle{ \nabla^{2}\theta-\frac{1}{\alpha_{s}}\frac{\partial \theta}{\partial \tau}=-\frac{g}{\kappa_{s}} }[/math]

Simple, direct application of this equation requires approximation. Additional terms arising in the transformed Laplacian are dropped, leaving the Laplacian in its conventional form.^[2]

Analytical solutions

Although analytical solutions can only be found for specific and simple cases, they give a good insight to deal with more complex situations. Analytical solutions for regular subsystems can also be combined to provide detailed descriptions of complex structures. In Prof. Batty's work,^[2] a Fourier series expansion to the temperature in the Laplace domain is introduced to find the solution to the linearized heat equation.

Example

This procedure can be applied to a simple but nontrivial case: an homogeneous cube die made out of GaAs, L=300 um. The goal is to find the temperature distribution on the top surface. The top surface is discretized into smaller squares with index i=1...N. One of them is considered to be the source.

Taking the Laplace transform to the heat equation:

[math]\displaystyle{ \nabla^{2}\bar{\Theta}-\frac{s}{k_{s}}\bar{\Theta}=0 }[/math]

where [math]\displaystyle{ \overline{\Theta}=s\theta-\theta\left(\tau=0\right) }[/math]

Function [math]\displaystyle{ \overline{\Theta} }[/math] is expanded in terms of cosine functions for the [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] variables and in terms of hyperbolic cosines and sines for [math]\displaystyle{ z }[/math] variable. Next, by applying adiabatic boundary conditions at the lateral walls and fix temperature at the bottom (heat sink temperature), thermal impedance matrix equation is derived:

[math]\displaystyle{ \Delta\theta_{i}=\sum_{j=1}^{N}R_{TH_{ij}}(t)P_{j}(t) }[/math]

Where the index [math]\displaystyle{ j }[/math] accounts for the power sources, while the index [math]\displaystyle{ i }[/math] refers to each small area.

For more details about the derivation, please see Prof. Batty's paper,.^[2] The below figure shows the steady state temperature distribution of this analytical method for a cubic die, with dimensions 300 um. A constant power source of 0.3W is applied over a central surface of dimension 0.1L x 0.1L. As expected, the distribution decays as it approaches to the boundaries, its maximum is located at the center and almost reaches 400K

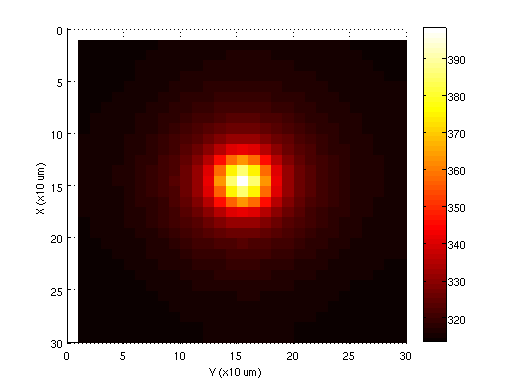
Numerical solutions

Numerical solutions use a mesh of the structure to perform the simulation. The most popular methods are: Finite difference time-domain (FDTD) method, Finite element method (FEM) and method of moments (MoM).

The finite-difference time-domain (FDTD) method is a robust and popular technique that consists in solving differential equations numerically as well as certain boundary conditions defined by the problem. This is done by discretizing the space and time, and using finite differencing formulas, thus the partial differential equations that describe the physics of the problem can be solved numerically by computer programs.

The FEM is also a numerical scheme employed to solve engineering and mathematical problems described by differential equations as well as boundary conditions. It discretizes the space into smaller elements for which basis functions are assigned to their nodes or edges. Basis functions are linear or higher order polynomials. Applying the differential equation and the boundary conditions of the problem to the basis functions, a system of equations is formulated using either the Ritz or Galerkin method. Finally, a direct or iterative method is employed to solve the system of linear equations.^[3] For the thermal case, FEM method is more suitable due to the nonlinearity nature of the thermal properties.

Example

The previous example can be solved with a numerical method. For this case, the cube can by discretized into rectangular elements. Its basis functions can be chosen to be a first order approximation (linear):

[math]\displaystyle{ N_{i}^{e}=\frac{1}{2}\xi\left(1\mp\zeta\right),\qquad i=1,4 }[/math]

[math]\displaystyle{ N_{i}^{e}=\frac{1}{2}\eta\left(1\mp\zeta\right),\qquad i=2,5 }[/math]

[math]\displaystyle{ N_{i}^{e}=\frac{1}{2}\left(1-\xi-\eta\right)\left(1\mp\zeta\right),\qquad i=3,6 }[/math]

where [math]\displaystyle{ \zeta=2(z-z_{c})/h_{z} }[/math]. If [math]\displaystyle{ z_{c}=0 }[/math], then [math]\displaystyle{ \zeta=2z/h_{z} }[/math].

Using this basis functions and after applying Galerkin's method to the heat transfer equation, a matrix equation is obtained:

[math]\displaystyle{ \left[S\right]\left\{ \theta\right\} +\left[R\right]\frac{d}{dt}\left\{ \theta\right\} =\left\{ B\right\} }[/math]

where,

[math]\displaystyle{ R_{ij}=\int_{v}N_{j} N_{i}dV }[/math]

[math]\displaystyle{ S_{ij}=k\int_{v}\nabla N_{j}.\nabla N_{i}dV }[/math]

[math]\displaystyle{ B_{i}=\frac{k}{\kappa_{s}}\int_{\Omega_{1}}N_{i}p(x,y)d\Omega+\frac{k}{\kappa_{s}}\int_{v}N_{i}gdV-kT_{o}\sum_{j=0}^{N_{D}}\int_{v}\nabla N_{j}^{D}.\nabla N_{i}dV }[/math].

This expressions can be evaluated by using a simple FEM code. For more details, please see.^[3] The figure below shows the temperature distribution for the numerical solution case. This solution shows very good agreement with the analytical case, its peak also reaches 390 K at the center. The apparent lack of smoothness of the distribution comes from the first order approximation of the basis functions and this can be solved by using higher order basis functions. Also, better results might be obtained by employing a denser mesh of the structure; however, for very dense meshes the computation time increases a lot, making the simulation non-practical.

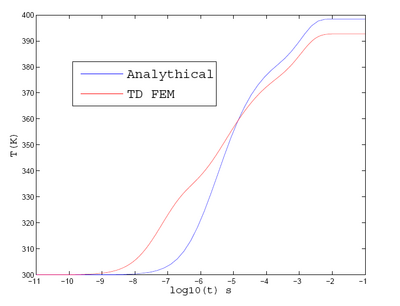
The next figure shows a comparison of the peak temperature as a function of time for both methods. The system reaches steady state in approximately [math]\displaystyle{ 1 ms }[/math].

Model order reduction

The numerical methods such as FEM or FDM derive a matrix equation as shown in the previous section. To solve this equation faster, a method called Model order reduction can be employed to find an approximation of lower order. This method is based on the fact that a high-dimensional state vector belongs to a low-dimensional subspace [1].

Figure below shows the concept of the MOR approximation: finding matrix V, the dimension of the system can be reduced to solve a simplified system.

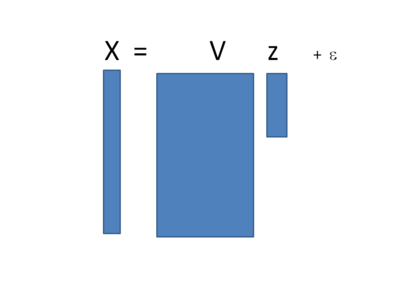
Therefore, the original system of equation:

[math]\displaystyle{ C\left\{ x\right\} '+K\left\{ x\right\} =F\left\{ u\right\} }[/math]

becomes:

[math]\displaystyle{ V^{T}CV\left\{ z\right\} '+V^{T}KV\left\{ z\right\} =V^{T}F\left\{ u\right\} }[/math]

Whose order is much lower than the original making the computation much less expensive. Once the solution is obtained, the original vector is found by taking the product with V.

Conclusion

The generation of heat is mainly produced by joule heating, this undesired effect has limited the performance of integrated circuits. In the preset article heat conduction was described and analytical and numerical methods to solve a heat transfer problem were presented. Using these methods, steady state temperature distribution was computed as well as the peak temperature as a function of time for a cubic die. For an input power of [math]\displaystyle{ 0.3 W }[/math] (or [math]\displaystyle{ 3.333e8 W/m_{2} }[/math]) applied over a single surface source on the top of a cubic die a peak increment of temperature in the order of 100 K was computed. Such increase in temperature can affect the behavior of surrounding semiconductor devices. Important parameters like mobility change drastically. That is why the heat dissipation is a relevant issue and must be considered for circuit designing.

See also

• Heat generation in integrated circuits

References

0.00 (0 votes) Original source: https://en.wikipedia.org/wiki/Thermal simulations for integrated circuits. Read more