Zome

A zome in the original sense is a building using unusual geometries^[1] (different from the standard house or other building which is essentially one or a series of rectangular boxes). The word "zome" was coined in 1968 by Steve Durkee, now known as Nooruddeen Durkee, combining the words dome and zonohedron.^{[citation needed]} One of the earliest models ended up as a large climbing structure at the Lama Foundation.^{[citation needed]}

Zometool is a construction set toy manufactured by Zometool, Inc. According to the company, Zometool was primarily designed for kids.^[2] Zometool has also been used in other fields, including fields of mathematics and physics.^[2] For example, aperiodic tilings such as Penrose tilings can be modeled using Zometool.^[3]

Both the building and the learning tool are the brainchildren of inventor/designer Steve Baer, his wife, Holly, and associates.

The term "Zome system" refers to the mathematics underlying the physical construction system.^{[citation needed]}

As building concept

Following his education at Amherst College and UCLA, Steve Baer studied mathematics at Eidgenössische Technische Hochschule (Zurich, Switzerland). Here he became interested in the possibilities of building innovative structures using polyhedra. Baer and his wife, Holly, moved back to the U.S., settling in Albuquerque, New Mexico in the early 1960s. In New Mexico, he experimented with constructing buildings of unusual geometries (calling them by his friend Steve Durkee's term: "zomes" — see "Drop City") — buildings intended to be appropriate to their environment, notably to utilize solar energy well. Baer was fascinated with the dome geometry popularized by architect R. Buckminster Fuller. Baer was an occasional guest at Drop City, an arts and experimental community near Trinidad, CO. He wanted to design and construct buildings that didn't suffer from some of the limitations of the smaller, owner-built versions of geodesic domes (of the 'pure Fuller' design).^{[citation needed]}

In recent years, the unconventional "zome" building-design approach with its multi-faceted geometric lines has been taken up by French builders in the Pyrenees. Home Work, a book published in 2004 and edited by Lloyd Kahn, has a section featuring these buildings. While many zomes built in the last couple decades have been wood-framed and made use of wood sheathing, much of what Baer himself originally designed and constructed involved metal framing with a sheet-metal outer skin.^{[citation needed]}

Zomes have also been used in the artistic, sculptural, and furniture areas. Zomadic, based in San Francisco, CA and founded by Rob Bell, incorporates zome geometry into artistic structures constructed primarily from CNC machined plywood components. Bell is a frequent attendee at Burning Man, a yearly artistic showcase event located in the Black Rock Desert of Nevada.^{[citation needed]}

Richie Duncan of Kodama Zomes, based in southern Oregon has invented a structural system based on a hanging zome geometry, suspended from an overhead anchor point. Constructed of metal compressive elements and webbing tensile elements, the structures are able to be assembled and disassembled. This suspended zome system has been used in furniture, performing arts, and treehouse applications.^{[citation needed]}

Yann Lipnick of Zomadic Concepts in France has an extensive study of, and multiple project construction of zomes in many different materials. He highlights the universal appeal and healing atmosphere that zomes provide, and has training classes and reference books on zome construction.^{[citation needed]}

Zometool Construction set

Zometool logo

The Great Grand Stellated 120-Cell modeled in Zometool

The Zometool plastic construction set toy is produced by a privately owned company of the same name, based outside of Longmont, Colorado, and which evolved out of Baer's company ZomeWorks. Its elements consist of small connector nodes and struts of various colors. The overall shape of a connector node is that of a non-uniform small rhombicosidodecahedron with each face replaced by a small hole. The ends of the struts are designed to fit in the holes of the connector nodes, allowing for syntheses of a variety of structures. The idea of shape-coding the three types of struts was developed by Marc Pelletier and Paul Hildebrandt. To create the "balls," or nodes, Pelletier and Hildebrandt invented a system of 62 hydraulic pins that came together to form a mold.^[4] The first connector node emerged from their mold perfectly on April 1, 1992.

In the years since 1992, Zometool has extended its product line, though the basic design of the connector node has not changed so all parts to date are compatible with each-other. From 1992 until 2000, Zometool produced kits with connector nodes and blue, yellow, and red struts. In 2000, Zometool introduced green struts, prompted by French architect Fabien Vienne, which can be used to construct the regular tetrahedron and octahedron. In 2003, Zometool changed the style of the struts slightly. The struts "with clicks" have a different surface texture and they also have longer nibs which allow for a more robust connection between connector node and strut.^[5]

Characteristics of Zometool

The color of a Zometool strut is associated with its cross section and also with the shape of the hole of the connector node in which it fits. Each blue strut has a rectangular cross section, each yellow strut has a triangular cross section, and each red strut has a pentagonal cross section. The cross section of a green strut is a rhombus of √2 aspect ratio, but as the connector nodes do not include holes at the required positions, the green struts instead fit into any of the 12 pentagonal holes with 5 possible orientations per hole, 60 possible orientations in all; using them is not as straightforward as the other struts.

At their midpoints, each of the yellow and red struts has a twist where the cross-sectional shape reverses. This design feature forces the connector nodes on the ends of the strut to have the same orientation. Similarly, the cross section of the blue strut is a non-square rectangle, again ensuring that the two nodes on the ends have the same orientation. Instead of a twist, the green struts have two bends which allow them to fit into the pentagonal holes of the connector node which are at a slight offset from the strut’s axis.

Among other places, the word zome comes from the term zone. The zome system allows no more than 61 zones. The cross-sectional shapes correspond to colors, and in turn these correspond to zone colors. Hence the zome system has 15 blue zones, 10 yellow zones, 6 red zones, and 30 green zones. Two shapes are associated with blue. The blue struts with a rectangular cross section are designed to lie in the same zones as the blue struts, but they are half the length of a blue strut; hence these struts are often called "half-blue" (and were originally made in a light blue color). The blue-green struts with a rhombic cross section lie in the same zones as the green struts, but they are designed so that the ratio of a rhombic blue-green strut to a blue strut is 1:1 (as opposed to the green strut's √2:1). It is important to understand that, due to this length ratio, the blue-green struts having a rhombic cross section do not mathematically belong to the zome system.^{[citation needed]}

A definition of the zome system

Here is a mathematical definition of the zome system, on which the physical Zometool construction set is based. It is defined in terms of the vector space [math]\displaystyle{ \R^3 }[/math], equipped with the standard inner product, also known as 3-dimensional Euclidean space.^{[citation needed]}

Let [math]\displaystyle{ \varphi }[/math] denote the Golden ratio and let [math]\displaystyle{ H_3 }[/math] denote the symmetry group of the configuration of vectors [math]\displaystyle{ (0,\pm\varphi,\pm 1) }[/math], [math]\displaystyle{ (\pm\varphi,\pm 1,0) }[/math], and [math]\displaystyle{ (\pm 1,0,\pm\varphi) }[/math]. The group [math]\displaystyle{ H_3 }[/math], an example of a Coxeter group, is known as the icosahedral group because it is the symmetry group of a regular icosahedron having these vectors as its vertices. The subgroup of [math]\displaystyle{ H_3 }[/math] consisting of the elements with determinant 1 (i.e. the rotations) is isomorphic to [math]\displaystyle{ A_5 }[/math].

Define the "standard blue vectors" as the [math]\displaystyle{ A_5 }[/math]-orbit of the vector [math]\displaystyle{ (2,0,0) }[/math]. Define the "standard yellow vectors" as the [math]\displaystyle{ A_5 }[/math]-orbit of the vector [math]\displaystyle{ (1,1,1) }[/math]. Define the "standard red vectors" as the [math]\displaystyle{ A_5 }[/math]-orbit of the vector [math]\displaystyle{ (0,\varphi,1) }[/math]. A "strut" of the zome system is any vector which can be obtained from the standard vectors described above by scaling by any power [math]\displaystyle{ \varphi^n }[/math], where [math]\displaystyle{ n }[/math] is an integer. A "node" of the zome system is any element of the subgroup of [math]\displaystyle{ \R^3 }[/math] generated by the struts. Finally, the "zome system" is the set of all pairs [math]\displaystyle{ (N,S) }[/math], where [math]\displaystyle{ N }[/math] is a set of nodes and [math]\displaystyle{ S }[/math] is a set of pairs [math]\displaystyle{ (v,w) }[/math] such that [math]\displaystyle{ v }[/math] and [math]\displaystyle{ w }[/math] are in [math]\displaystyle{ N }[/math] and the difference [math]\displaystyle{ v-w }[/math] is a strut.

One may check that there are 30, 20, and 12 standard vectors having the colors blue, yellow, and red, respectively. Correspondingly, the stabilizer subgroup of a blue, yellow, or red strut is isomorphic to the cyclic group of order 2, 3, or 5, respectively. Hence, one may also describe the blue, yellow, and red struts as "rectangular", "triangular", and "pentagonal", respectively.

One may extend the zome system by adjoining green vectors. The "standard green vectors" comprise the [math]\displaystyle{ A_5 }[/math]-orbit of the vector [math]\displaystyle{ (2,2,0) }[/math] and a "green strut" as any vector which can be obtained by scaling a standard green vector by any integral power [math]\displaystyle{ \varphi^n }[/math]. As above, one may check that there are [math]\displaystyle{ |A_5| }[/math]=60 standard green vectors. One may then enhance the zome system by including these green struts. Doing this does not affect the set of nodes.

The abstract zome system defined above is significant because of the following fact: Every connected zome model has a faithful image in the zome system. The converse of this fact is only partially true, but this is due only to the laws of physics. For example, the radius of a zometool node is positive (as opposed to a node being a single point mathematically), so one cannot make a zometool model where two nodes are separated by an arbitrarily small prescribed distance. Similarly, only a finite number of lengths of struts will ever be manufactured, and a green strut cannot be placed directly adjacent to a red strut or another green strut with which it shares the same hole (even though they are mathematically distinct).^{[citation needed]}

Zome as a modeling system

Compound of five cubes, rendered in ZomeCAD

Compound of five tetrahedra, rendered in vZome

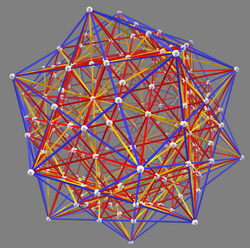
The zome system is especially good at modeling 1-dimensional skeleta of highly symmetric objects in 3- and 4-dimensional Euclidean space. The most prominent among these are the five Platonic solids, and the 4-dimensional polytopes related to the 120-cell and the 600-cell. However, the list of mathematical objects which are amenable to zome is long, and an exhaustive list is not forthcoming. Besides those already mentioned, one may use zome to model the following mathematical objects:^{[citation needed]}

• Three of the four Kepler-Poinsot polyhedra
• Regular polyhedral compounds
• Regular 4-dimensional polytopes and some compounds
• Many stellations of the rhombic triacontahedron
• Many stellations of the regular icosahedron
• Zonohedra, especially the rhombic enneacontahedron and rhombic triacontahedron
• Hypercubes in dimensions 61 or fewer
• Most uniform polyhedra (a major exception being those formed using the snub operation)
• Many uniform 4-polytopes
• Thorold Gosset's exceptional semiregular polytopes in 6, 7, and 8 dimensions
• A few of the Johnson solids
• Desargues configuration
• Two of the Catalan solids
• Classical and exceptional root systems
• Triality (from Lie theory)

Other uses of zome

The uses of zome are not restricted to pure mathematics. Other uses include the study of engineering problems, especially steel-truss structures, the study of some molecular, nanotube, and viral structures, and to make soap film surfaces.^{[citation needed]}

Notes

References

• Steve Baer. Zome Primer. Zomeworks Corporation, 1970.
• David Booth. "The New Zome Primer," in Fivefold Symmetry, István Hargittai (editor). World Scientific Publishing Company, 1992.
• Coxeter, H. S. M. Regular Polytopes, 3rd edition, Dover, 1973. ISBN:0-486-61480-8.
• Brian C. Hall. Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Springer, 2003. ISBN:0-387-40122-9.
• George Hart, Four-Dimensional Polytope Projection Barn Raisings. Proceedings, Sixth International Conference of the Society of Art, Math, and Architecture, Texas A&M University. May 2007.
• George Hart and Henri Picciotto. Zome Geometry: Hands-on Learning with Zome Models. Key Curriculum Press, 2001. ISBN:1-55953-385-4.
• Paul R. Hildebrandt & Marc G. Pelletier (1985). "Geometric Modeling Kit and Method of Making Same". United States Patent No. 4,701,131.
• Paul Hildebrandt. Zome-inspired Sculpture. Proceedings, Bridges London: Connections between Mathematics, Art, and Music, Reza Sarhangi and John Sharp (editors). (2006) 335–342.
• Paul Hildebrandt & Clark Richert (2012). "Domes, Zomes, and Drop City". Bridges 2012.
• Cass Wester (1973). "Steve Baer and Holly Baer: Dome Home Enthusiasts". Mother Earth News 22.
• David A. Richter. Two results concerning the Zome model of the 600-cell. Proceedings, Renaissance Banff: Mathematical Connections between Mathematics, Art, and Music, Robert Moody and Reza Sarhangi (editors). (2005) 419–426.
• David A. Richter and Scott Vorthmann. Green Quaternions, Tenacious Symmetry, and Octahedral Zome. Proceedings, Bridges London: Connections between Mathematics, Art, and Music, Reza Sarhangi and John Sharp (editors). (2006) 429–436.
• Steven F. Rogers & Paul R. Hildebrandt (2002) "Connections for Geometric Modeling Kit". United States Patent No. 6,840,699 B2.
• Sadler, Simon (2006). "Drop City Revisited". Journal of Architectural Education 59 (3), pp. 5-14.
• Michael Stranahan, Carlos Neumann, & Paul Hildebrandt (2011). "How Not to Bring Your Product to Market". Bridges 2011.

External links

Zome buildings:

• The zome building concept explained
• Examples of European zome buildings
• Examples of zome usage in North American prefabricated housing construction

Zomes as art:

• Kodama Zomes
• Zomadic
• Heliss

Zome modelling system:

• Zome modelisation - Zome modelisation - Open-Source Sketchup Plugin
• Zome Creator - Source code for free Zome modelisation software
• Weisstein, Eric W.. "Zome". http://mathworld.wolfram.com/Zome.html. 
• Zometool The manufacturer's site.
• Advanced Zome Projects by David Richter
• Zome Geometry by George W. Hart and Henri Picciotto
• vZome for building virtual Zome models
• Zome at Bridges London at the London Knowledge Lab
• Japan Zome Club a user's club in Japan (Japanese)
• Metazome a project making Zome models with Zome

Energy Management Company:'

• [1] ZOME Energy Networks, a smart energy company

0.00 (0 votes)